Hostname: page-component-5f745c7db-sbzbt Total loading time: 0 Render date: 2025-01-06T07:57:31.526Z Has data issue: true hasContentIssue false
  • English
  • Français

Linear instability of a supersonic boundary layer over a rotating cone

Published online by Cambridge University Press:  18 January 2023

Runjie Song Open the ORCID record for Runjie Song [Opens in a new window]  and
Ming Dong Open the ORCID record for Ming Dong [Opens in a new window]
Runjie Song
Affiliation:
State Key laboratory of Nonlinear Mechanics, Institute of Mechanics, Chinese Academy of Sciences, Beijing 100190, PR China
Ming Dong*
Affiliation:
State Key laboratory of Nonlinear Mechanics, Institute of Mechanics, Chinese Academy of Sciences, Beijing 100190, PR China Sino-Russian Mathematics Center, Peking University, Beijing 100871, PR China
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

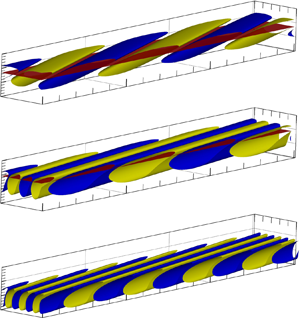
In this paper, we conduct a systematic study of the instability of a boundary layer over a rotating cone that is inserting into a supersonic stream with zero angle of attack. The base flow is obtained by solving the compressible boundary-layer equations using a marching scheme, whose accuracy is confirmed by comparing with the full Navier–Stokes solution. Setting the oncoming Mach number and the semi-apex angle to be 3 and 7$^\circ$, respectively, the instability characteristics for different rotating rates ($\bar \varOmega$, defined as the ratio of the rotating speed of the cone to the axial velocity) and Reynolds numbers ($R$) are revealed. For a rather weak rotation, $\bar \varOmega \ll 1$, only the modified Mack mode (MMM) exists, which is an extension of the supersonic Mack mode in a quasi-two-dimensional boundary layer to a rotation configuration. Further increase of $\bar \varOmega$ leads to the appearance of a cross-flow mode (CFM), coexisting with the MMM but in the quasi-zero frequency band. The unstable zones of the MMM and CFM merge together, and so they are referred to as the type-I instability. When $\bar \varOmega$ is increased to an $O(1)$ level, an additional unstable zone emerges, which is referred to as the type-II instability to be distinguished from the aforementioned type-I instability. The type-II instability appears as a centrifugal mode (CM) when $R$ is less than a certain value, but appears as a new CFM for higher Reynolds numbers. The unstable zone of the type-II CM enlarges as $\bar \varOmega$ increases. The vortex structures of these types of instability modes are compared, and their large-$R$ behaviours are also discussed.

JFM classification

Boundary Layers: Boundary layer stability Compressible Flows: Compressible boundary layers Instability: Shear-flow instability
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 955 , 25 January 2023 , A31
Check for updates
Copyright
© The Author(s), 2023. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Anderson, J.D. 1990 Modern Compressible Flow: With Historical Perspective, pp. 294–306. McGraw-Hill Book Company.Google Scholar
Babcock, K.L., Ahlers, G. & Cannell, D.S. 1991 Noise-sustained structure in Taylor–Couette flow with through flow. Phys. Rev. Lett. 67, 3388–3391.CrossRefGoogle ScholarPubMed
Balakumar, P. & Owens, L. 2010 Stability of hypersonic boundary layers on a cone at an angle of attack. AIAA paper 2010-4718.CrossRefGoogle Scholar
Balakumar, P. & Reed, H.L. 1991 Stability of three-dimensional supersonic boundary layers. Phys. Fluids 3 (4), 617–632.CrossRefGoogle Scholar
Butler, A. & Wu, X. 2018 Stationary crossflow vortices near the leading edge of three-dimensional boundary layers: the role of non-parallelism and excitation by surface roughness. J. Fluid Mech. 845, 93–140.CrossRefGoogle Scholar
Choudhari, M. 1995 Long-wavelength asymptotics of unstable crossflow modes, including the effect of surface curvature. Proc. R. Soc. Lond. 451 (1943), 515–541.Google Scholar
Corke, T.C. & Knastak, K.F. 1998 Stationary travelling cross-flow mode interactions on a rotating disk. J. Fluid Mech. 355, 285–315.CrossRefGoogle Scholar
Cowley, S. & Hall, P. 1990 On the instability of hypersonic flow past a wedge. J. Fluid Mech. 214, 17–42.CrossRefGoogle Scholar
Craig, S.A. & Saric, W.S. 2016 Crossflow instability in a hypersonic boundary layer. J. Fluid Mech. 808, 224–244.CrossRefGoogle Scholar
Dong, M., Liu, Y. & Wu, X. 2020 Receptivity of inviscid modes in supersonic boundary layers due to scattering of free-stream sound by localised wall roughness. J. Fluid Mech. 896, A23.CrossRefGoogle Scholar
Dong, M. & Zhao, L. 2021 An asymptotic theory of the roughness impact on inviscid Mack modes in supersonic/hypersonic boundary layers. J. Fluid Mech. 913, A22.CrossRefGoogle Scholar
Fedorov, A. 2011 Transition and stability of high-speed boundary layers. Annu. Rev. Fluid Mech. 43, 79–95.CrossRefGoogle Scholar
Gajjar, J. 1996 Nonlinear stability of nonstationary cross-flow vortices in compressible boundary layers. Stud. Appl. Maths 96 (1), 53–84.CrossRefGoogle Scholar
Gajjar, J., Arebi, M. & Sibanda, P. 1996 Nonlinear development of cross-flow instabilities in compressible and incompressible boundary layer flows. AIAA paper 1996-2159.CrossRefGoogle Scholar
Garrett, S.J., Hussain, Z. & Stephen, S.O. 2009 The cross-flow instability of the boundary layer on a rotating cone. J. Fluid Mech. 622, 209–232.CrossRefGoogle Scholar
Garrett, S.J., Hussain, Z. & Stephen, S.O. 2010 Boundary-layer transition on broad cones rotating in an imposed axial flow. AIAA J. 48 (6), 1184–1194.CrossRefGoogle Scholar
Garrett, S.J. & Peake, N. 2007 The absolute instability of the boundary layer on a rotating cone. Eur. J. Mech. (B/Fluids) 26 (3), 344–353.CrossRefGoogle Scholar
Goldstein, M.E. & Leib, S.J. 1989 Nonlinear evolution of oblique waves on compressible shear layers. J. Fluid Mech. 207, 73–96.CrossRefGoogle Scholar
Gregory, N., Stuart, J.T., Walker, W.S. & Bullard, E.C. 1955 On the stability of three-dimensional boundary layers with application to the flow due to a rotating disk. Phil. Trans. R. Soc. Lond. A 248 (943), 155–199.Google Scholar
Hall, P. 1982 Taylor–Görtler vortices in fully developed or boundary-layer flows: linear theory. J. Fluid Mech. 124, 475–494.CrossRefGoogle Scholar
Hall, P. 1983 The linear development of Görtler vortices in growing boundary layers. J. Fluid Mech. 130, 41–58.CrossRefGoogle Scholar
Hall, P. 1986 An asymptotic investigation of the stationary modes of instability of the boundary layer on a rotating disc. Proc. R. Soc. Lond. A 406 (1830), 93–106.Google Scholar
Hussain, Z., Garrett, S.J. & Stephen, S.O. 2014 The centrifugal instability of the boundary-layer flow over slender rotating cones. J. Fluid Mech. 755, 274–293.CrossRefGoogle Scholar
Hussain, Z., Garrett, S.J., Stephen, S.O. & Griffiths, P.T. 2016 The centrifugal instability of the boundary-layer flow over a slender rotating cone in an enforced axial free stream. J. Fluid Mech. 788, 70–94.CrossRefGoogle Scholar
Kachanov, Y.S. 1994 Physical mechanisms of laminar-boundary-layer transition. Annu. Rev. Fluid Mech. 26 (1), 411–482.CrossRefGoogle Scholar
Kato, K., Alfredsson, P.H. & Lingwood, R.J. 2019 a Boundary-layer transition over a rotating broad cone. Phys. Rev. Fluids 4, 071902.CrossRefGoogle Scholar
Kato, K., Kawata, T., Alfredsson, P.H. & Lingwood, R.J. 2019 b Investigation of the structures in the unstable rotating-cone boundary layer. Phys. Rev. Fluids 4, 053903.CrossRefGoogle Scholar
Kato, K., Segalini, A., Alfredsson, P.H. & Lingwood, R.J. 2021 Instability and transition in the boundary layer driven by a rotating slender cone. J. Fluid Mech. 915, R4.CrossRefGoogle Scholar
Klatt, D., Hruschka, R. & Leopold, F. 2012 Numerical and experimental investigation of the Magnus effect in supersonic flows. AIAA paper 2012-3230.CrossRefGoogle Scholar
Kobayashi, R. 1994 Review: laminar-to-turbulent transition of three-dimensional boundary layers on rotating bodies. Trans. ASME J. Fluids Engng 116 (2), 200–211.CrossRefGoogle Scholar
Kobayashi, R. & Izumi, H. 1983 Boundary-layer transition on a rotating cone in still fluid. J. Fluid Mech. 127, 353–364.CrossRefGoogle Scholar
Kobayashi, R., Kohama, Y. & Kurosawa, M. 1983 Boundary-layer transition on a rotating cone in axial flow. J. Fluid Mech. 127, 341–352.CrossRefGoogle Scholar
Kobayashi, R., Kohama, Y. & Takamadate, C. 1980 Spiral vortices in boundary layer transition regime on a rotating disk. Acta Mech. 35, 71–82.CrossRefGoogle Scholar
Kohama, Y. 1987 Some expectation on the mechanism of cross-flow instability in a swept wing flow. Acta Mech. 66, 21–28.CrossRefGoogle Scholar
Lees, L. & Lin, C.C. 1946 Investigation of the stability of the laminar boundary layer in a compressible fluid. Tech. Rep. Tech. Rep. TN-1115. NASA Technical Memorandum.Google Scholar
Li, S. & Dong, M. 2021 Verification of local scattering theory as is applied to transition prediction in hypersonic boundary layers (in Chinese). Adv. Mech. 51, 364.Google Scholar
Lingwood, R.J. 1995 Absolute instability of the boundary layer on a rotating disk. J. Fluid Mech. 299, 17–33.CrossRefGoogle Scholar
Lingwood, R.J. 1996 An experimental study of absolute instability of the rotating-disk boundary-layer flow. J. Fluid Mech. 314, 373–405.CrossRefGoogle Scholar
Liu, Y., Dong, M. & Wu, X. 2020 Generation of first Mack modes in supersonic boundary layers by slow acoustic waves interacting with streamwise isolated wall roughness. J. Fluid Mech. 888, A10.CrossRefGoogle Scholar
Mack, L.M. 1987 Review of linear compressible stability theory. In Stability of Time Dependent and Spatially Varying Flows (ed. D.L. Dwoyer & M.Y. Hussaini), pp. 164–187.Google Scholar
Malik, M.R. 1986 The neutral curve for stationary disturbances in rotating-disk flow. J. Fluid Mech. 164, 275–287.CrossRefGoogle Scholar
Malik, M.R. 1990 Numerical methods for hypersonic boundary layer stability. J. Comput. Phys. 86 (2), 376–413.CrossRefGoogle Scholar
Malik, M.R., Li, F. & Chang, C.-L. 1994 Crossflow disturbances in three-dimensional boundary layers: nonlinear development, wave interaction and secondary instability. J. Fluid Mech. 268, 1–36.CrossRefGoogle Scholar
Malik, M.R., Wilkinson, S.P. & Orszag, S.A. 1981 Instability and transition in rotating disk flow. AIAA J. 19 (9), 1131–1138.CrossRefGoogle Scholar
Morgan, S., Davies, C. & Thomas, C. 2021 Control of stationary convective instabilities in the rotating disk boundary layer via time-periodic modulation. J. Fluid Mech. 925, A20.CrossRefGoogle Scholar
Pruett, D.C. 1994 A spectrally accurate boundary-layer code for infinite swept wings. Tech. Rep. NASA-CR-195014. NASA Technical Memorandum.Google Scholar
Reed, H.L. & Saric, W.S. 1989 Stability of three-dimensional boundary layers. Annu. Rev. Fluid Mech. 21 (1), 235–284.CrossRefGoogle Scholar
Saric, W.S., Reed, H.L. & White, E.B. 2003 Stability and transition of three-dimensional boundary layers. Annu. Rev. Fluid Mech. 35 (1), 413–440.CrossRefGoogle Scholar
Sims, J.L. 1964 Tables for supersonic flow around right circular cones at zero angle of attack. Tech. Rep. NASA-SP-3004. NASA Technical Memorandum.Google Scholar
Sivasubramanian, J. & Fasel, H.F. 2015 Direct numerical simulation of transition in a sharp cone boundary layer at Mach 6: fundamental breakdown. J. Fluid Mech. 768, 175–218.CrossRefGoogle Scholar
Smith, F.T. 1979 On the non-parallel flow stability of the blasius boundary layer. Phil. Trans. R. Soc. Lond. A 366 (1724), 91–109.Google Scholar
Smith, F.T. 1989 On the first-mode instability in subsonic, supersonic or hypersonic boundary layers. J. Fluid Mech. 198, 127–153.CrossRefGoogle Scholar
Smith, F.T. & Brown, S.N. 1990 The inviscid instability of a blasius boundary layer at large values of the Mach number. J. Fluid Mech. 219, 499–518.CrossRefGoogle Scholar
Song, R., Zhao, L. & Huang, Z. 2020 Secondary instability of stationary Görtler vortices originating from first/second Mack mode. Phys. Fluids 32 (3), 034109.Google Scholar
Sturek, W.B., Dwyer, H.A., Kayser, L.D., Nietubicz, C.J., Reklis, R.P. & Opalka, K.O. 1978 Computations of Magnus effects for a yawed, spinning body of revolution. AIAA J. 16 (7), 687–692.CrossRefGoogle Scholar
Tambe, S., Schrijer, F., Rao, A.R. & Veldhuis, L. 2021 Boundary layer instability over a rotating slender cone under non-axial inflow. J. Fluid Mech. 910, A25.CrossRefGoogle Scholar
Taylor, G.I. 1923 Stability of a viscous liquid contained between two rotating cylinders. Phil. Trans. R. Soc. Lond. A 102 (718), 541–542.Google Scholar
Thomas, C. & Davies, C. 2021 An adjoint approach for computing the receptivity of the rotating disc boundary layer to surface roughness. J. Fluid Mech. 926, A16.CrossRefGoogle Scholar
Towers, P.T. 2013 The stability and transition of the compressible boundary-layer flow over broad rotating cones. PhD thesis, University of Leicester.CrossRefGoogle Scholar
Tsameret, A. & Steinberg, V. 1994 Absolute and convective instabilities and noise-sustained structures in the Couette–Taylor system with an axial flow. Phys. Rev. E 49, 1291–1308.CrossRefGoogle ScholarPubMed
Turkyilmazoglu, M. 2005 Lower branch modes of the compressible boundary layer flow due to a rotating-disk. Stud. Appl. Maths 114 (1), 17–43.CrossRefGoogle Scholar
Turkyilmazoglu, M. 2007 Influence of finite amplitude disturbances on the nonstationary modes of a compressible boundary layer flow. Stud. Appl. Maths 118 (3), 199–220.CrossRefGoogle Scholar
Turkyilmazoglu, M., Cole, J.W. & Gajjar, J.S.B. 2000 Absolute and convective instabilities in the compressible boundary layer on a rotating disk. Theor. Comput. Fluid Dyn. 14, 21–37.CrossRefGoogle Scholar
Wu, X. 2019 Nonlinear theories for shear flow instabilities: physical insights and practical implications. Annu. Rev. Fluid Mech. 51 (1), 451–485.CrossRefGoogle Scholar
Wu, X. & Dong, M. 2016 A local scattering theory for the effects of isolated roughness on boundary-layer instability and transition: transmission coefficient as an eigenvalue. J. Fluid Mech. 794, 68–108.CrossRefGoogle Scholar
Wu, X., Zhao, D. & Luo, J. 2011 Excitation of steady and unsteady Görtler vortices by free-stream vortical disturbances. J. Fluid Mech. 682, 66–100.CrossRefGoogle Scholar
Xu, D., Zhang, Y. & Wu, X. 2017 Nonlinear evolution and secondary instability of steady and unsteady Görtler vortices induced by free-stream vortical disturbances. J. Fluid Mech. 829, 681–730.CrossRefGoogle Scholar
Zhao, L. & Dong, M. 2022 Effect of surface temperature strips on the evolution of supersonic and hypersonic Mack modes: asymptotic theory and numerical results. Phys. Rev. Fluids 7, 053901.CrossRefGoogle Scholar
Zhong, X. & Wang, X. 2012 Direct numerical simulation on the receptivity, instability, and transition of hypersonic boundary layers. Annu. Rev. Fluid Mech. 44 (1), 527–561.CrossRefGoogle Scholar