Article contents
Linear global and asymptotic stability analysis of the flow past rectangular cylinders moving along a wall
Published online by Cambridge University Press: 29 June 2023
Abstract
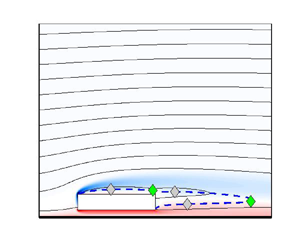
The primary instability of the steady two-dimensional flow past rectangular cylinders moving parallel to a solid wall is studied, as a function of the cylinder length-to-thickness aspect ratio  ${A{\kern-4pt}R} =L/D$ and the dimensionless distance from the wall
${A{\kern-4pt}R} =L/D$ and the dimensionless distance from the wall  $g=G/D$. For all
$g=G/D$. For all  ${A{\kern-4pt}R}$, two kinds of primary instability are found: a Hopf bifurcation leading to an unsteady two-dimensional flow for
${A{\kern-4pt}R}$, two kinds of primary instability are found: a Hopf bifurcation leading to an unsteady two-dimensional flow for  $g \ge 0.5$, and a regular bifurcation leading to a steady three-dimensional flow for
$g \ge 0.5$, and a regular bifurcation leading to a steady three-dimensional flow for  $g < 0.5$. The critical Reynolds number
$g < 0.5$. The critical Reynolds number  $Re_{c,2\text{-}D}$ of the Hopf bifurcation (
$Re_{c,2\text{-}D}$ of the Hopf bifurcation ( $Re=U_\infty D/\nu$, where
$Re=U_\infty D/\nu$, where  $U_\infty$ is the free stream velocity,
$U_\infty$ is the free stream velocity,  $D$ the cylinder thickness and
$D$ the cylinder thickness and  $\nu$ the kinematic viscosity) changes with the gap height and the aspect ratio. For
$\nu$ the kinematic viscosity) changes with the gap height and the aspect ratio. For  ${A{\kern-4pt}R} \le 1$,
${A{\kern-4pt}R} \le 1$,  $Re_{c,2\text{-}D}$ increases monotonically when the gap height is reduced. For
$Re_{c,2\text{-}D}$ increases monotonically when the gap height is reduced. For  ${A{\kern-4pt}R} >1$,
${A{\kern-4pt}R} >1$,  $Re_{c,2\text{-}D}$ decreases when the gap is reduced until
$Re_{c,2\text{-}D}$ decreases when the gap is reduced until  $g \approx 1.5$, and then it increases. The critical Reynolds number
$g \approx 1.5$, and then it increases. The critical Reynolds number  $Re_{c,3\text{-}D}$ of the three-dimensional regular bifurcation decreases monotonically for all
$Re_{c,3\text{-}D}$ of the three-dimensional regular bifurcation decreases monotonically for all  ${A{\kern-4pt}R}$, when the gap height is reduced below
${A{\kern-4pt}R}$, when the gap height is reduced below  $g < 0.5$. For small gaps,
$g < 0.5$. For small gaps,  $g < 0.5$, the hyperbolic/elliptic/centrifugal character of the regular instability is investigated by means of a short-wavelength approximation considering pressureless inviscid modes. For elongated cylinders,
$g < 0.5$, the hyperbolic/elliptic/centrifugal character of the regular instability is investigated by means of a short-wavelength approximation considering pressureless inviscid modes. For elongated cylinders,  ${A{\kern-4pt}R} > 3$, the closed streamline related to the maximum growth rate is located within the top recirculating region of the wake, and includes the flow region with maximum structural sensitivity; the asymptotic analysis is in very good agreement with the global stability analysis, assessing the inviscid character of the instability. For cylinders with
${A{\kern-4pt}R} > 3$, the closed streamline related to the maximum growth rate is located within the top recirculating region of the wake, and includes the flow region with maximum structural sensitivity; the asymptotic analysis is in very good agreement with the global stability analysis, assessing the inviscid character of the instability. For cylinders with  $AR \leq 3$, however, the local analysis fails to predict the three-dimensional regular bifurcation.
$AR \leq 3$, however, the local analysis fails to predict the three-dimensional regular bifurcation.
JFM classification
- Type
- JFM Papers
- Information
- Copyright
- © The Author(s), 2023. Published by Cambridge University Press
Footnotes
Present address: Complex Fluids and Flows Unit, Okinawa Institute of Science and Technology Graduate University, 1919-1 Tancha, Onna-son, Okinawa 904-0495, Japan.
References
- 2
- Cited by



