Article contents
Linear and nonlinear responses to harmonic force in rotating flow
Published online by Cambridge University Press: 04 May 2016
Abstract
For understanding the dissipation in a rotating flow when resonance occurs, we study the rotating flow driven by the harmonic force in a periodic box. Both the linear and nonlinear regimes are studied. The various parameters such as the force amplitude  $a$, the force frequency
$a$, the force frequency  ${\it\omega}$, the force wavenumber
${\it\omega}$, the force wavenumber 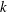 $k$ and the Ekman number
$k$ and the Ekman number 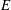 $E$ are investigated. In the linear regime, the dissipation at the resonant frequency scales as
$E$ are investigated. In the linear regime, the dissipation at the resonant frequency scales as 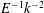 $E^{-1}k^{-2}$, and it is much stronger than the dissipation at the non-resonant frequencies on large scales and at low Ekman numbers. In the nonlinear regime, at the resonant frequency the effective dissipation (dissipation normalised with the square of the force amplitude) is lower than in the linear regime and it decreases with increasing force amplitude. This nonlinear suppression effect is significant near the resonant frequency but negligible far away from the resonant frequency. Opposite to the linear regime, in the nonlinear regime at the resonant frequency the lower Ekman number leads to lower dissipation because of the stronger nonlinear effect. This work implies that the previous linear calculations overestimated the tidal dissipation, which is important for understanding the tides in stars and giant planets.
$E^{-1}k^{-2}$, and it is much stronger than the dissipation at the non-resonant frequencies on large scales and at low Ekman numbers. In the nonlinear regime, at the resonant frequency the effective dissipation (dissipation normalised with the square of the force amplitude) is lower than in the linear regime and it decreases with increasing force amplitude. This nonlinear suppression effect is significant near the resonant frequency but negligible far away from the resonant frequency. Opposite to the linear regime, in the nonlinear regime at the resonant frequency the lower Ekman number leads to lower dissipation because of the stronger nonlinear effect. This work implies that the previous linear calculations overestimated the tidal dissipation, which is important for understanding the tides in stars and giant planets.
- Type
- Papers
- Information
- Copyright
- © 2016 Cambridge University Press
References
- 4
- Cited by



