1 Introduction
The evaporation of sessile droplets has been the subject of increasing theoretical and experimental research activity in recent years (see, for example, Cazabat & Guéna Reference Cazabat and Guéna2010, Erbil Reference Erbil2012, Larson Reference Larson2014 and Lohse & Zhang Reference Lohse and Zhang2015). In particular, there is growing interest in how the evolution, and hence the lifetimes, of evaporating droplets depend on the thermal properties of the system.
In their pioneering work on the evaporation of sessile droplets, Picknett & Bexon (Reference Picknett and Bexon1977) calculated the lifetimes of droplets evaporating in the so-called extreme modes of evaporation, namely the constant contact radius (CR) and constant contact angle (CA) modes. In practice, however, droplets often evaporate in the so-called stick–slide (SS) mode consisting of a CR phase followed by a CA phase (see, for example, Nguyen & Nguyen Reference Nguyen and Nguyen2012 and Dash & Garimella Reference Dash and Garimella2013), and so Stauber et al. (Reference Stauber, Wilson, Duffy and Sefiane2014, Reference Stauber, Wilson, Duffy and Sefiane2015) calculated the lifetime of a droplet evaporating in this mode. Other modes of evaporation can, of course, also occur, notably the so-called stick–jump (SJ) mode in which the droplet evaporates in a series of stick (i.e. CR) phases separated by jump phases in which the contact angle and contact radius jump instantaneously (see, for example, Askounis et al. Reference Askounis, Orejon, Koutsos, Sefiane and Shanahan2011, Orejon, Sefiane and Shanahan Reference Orejon, Sefiane and Shanahan2011 and Dietrich et al. Reference Dietrich, Kooij, Zhang, Zandvliet and Lohse2015), and so Stauber (Reference Stauber2015) performed the corresponding analysis of a droplet evaporating in this mode. However, all of these works use the basic diffusion-limited model for droplet evaporation (see, for example, Popov Reference Popov2005) which does not account for the variation of the saturation concentration of the vapour with temperature. As a result, none of these works accounts for the influence of the thermal properties of the system on the evaporation of the droplets, which can be significant (see, for example, Dunn et al. Reference Dunn, Wilson, Duffy, David and Sefiane2008, Reference Dunn, Wilson, Duffy, David and Sefiane2009a ,Reference Dunn, Wilson, Duffy and Sefiane b , Sefiane & Bennacer Reference Sefiane and Bennacer2011, Sobac & Brutin Reference Sobac and Brutin2012, Ait Saada, Chikh and Tadrist Reference Ait Saada, Chikh and Tadrist2013, Lopes et al. Reference Lopes, Bonaccurso, Gambaryan-Roisman and Stephan2013 and Diddens et al. Reference Diddens, Tan, Lv, Versluis, Kuerten, Zhang and Lohse2017). The aim of the present work is to gain further insight into this issue by using an extended model to obtain asymptotic solutions for the evolution, and hence explicit expressions for the lifetimes, of droplets when the influence of the thermal properties of the system is strong.
2 Problem formulation
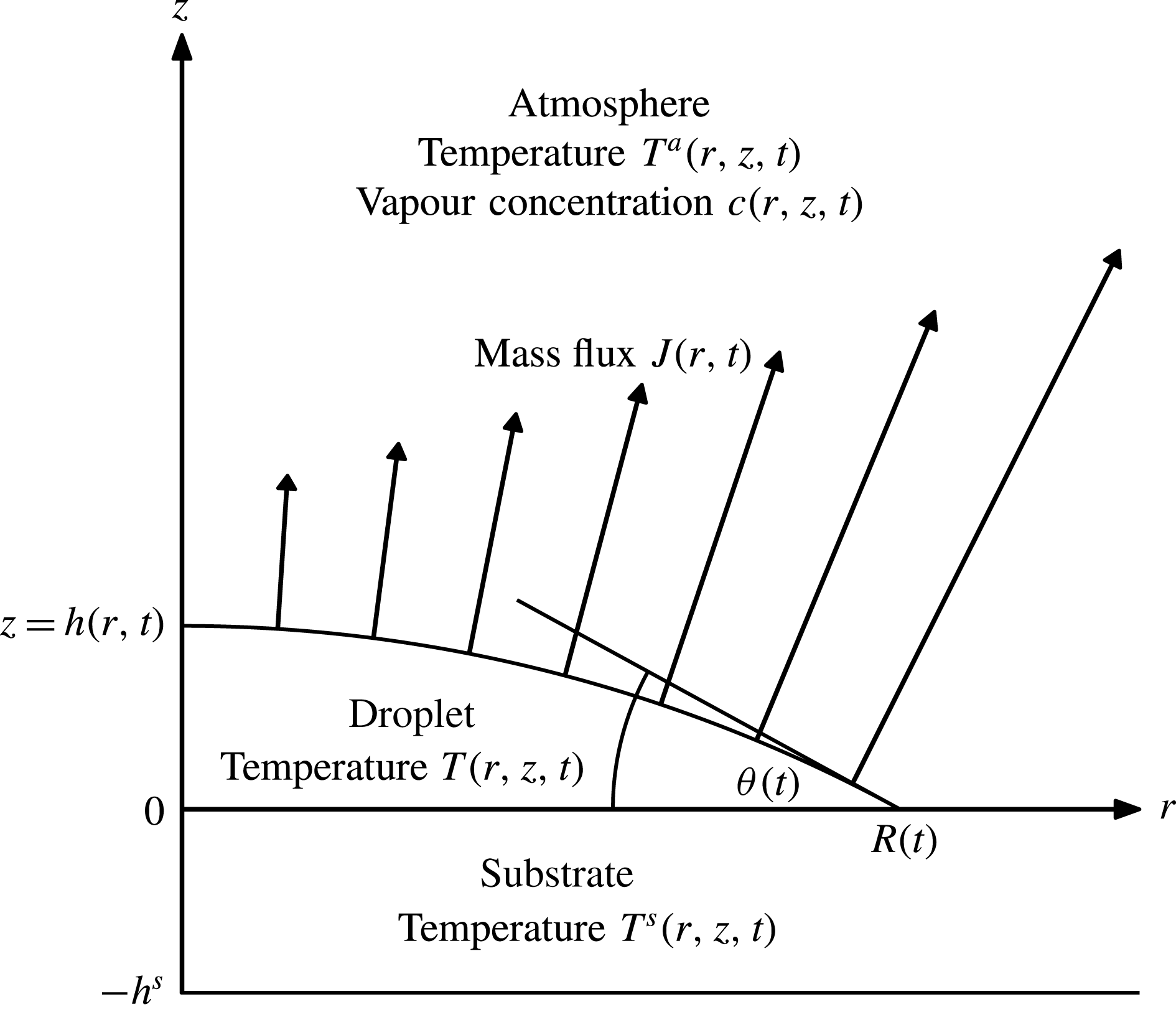
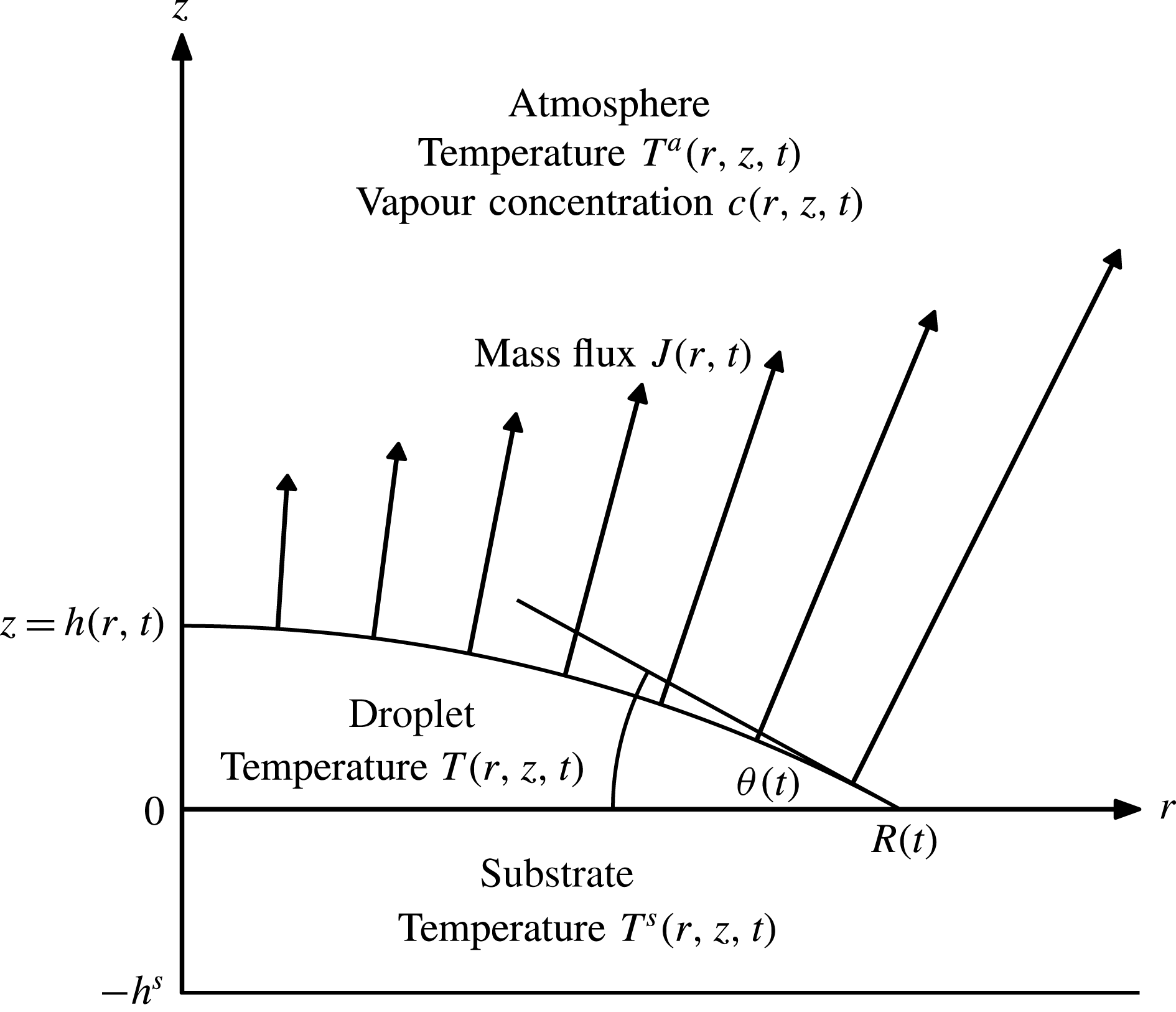
Figure 1. The geometry of a evaporating thin sessile droplet on a thin substrate.
Consider the quasi-steady evaporation of a small thin axisymmetric sessile droplet with radius
![]() $R=R(t)$
, contact angle
$R=R(t)$
, contact angle
![]() $\unicode[STIX]{x1D703}=\unicode[STIX]{x1D703}(t)$
and volume
$\unicode[STIX]{x1D703}=\unicode[STIX]{x1D703}(t)$
and volume
![]() $V=V(t)$
of a fluid with constant surface tension
$V=V(t)$
of a fluid with constant surface tension
![]() $\unicode[STIX]{x1D70E}$
, density
$\unicode[STIX]{x1D70E}$
, density
![]() $\unicode[STIX]{x1D70C}$
and thermal conductivity
$\unicode[STIX]{x1D70C}$
and thermal conductivity
![]() $k$
on a thin substrate with constant thickness
$k$
on a thin substrate with constant thickness
![]() $h^{s}$
and thermal conductivity
$h^{s}$
and thermal conductivity
![]() $k^{s}$
in a quiescent atmosphere with thermal conductivity
$k^{s}$
in a quiescent atmosphere with thermal conductivity
![]() $k^{a}$
. Using cylindrical polar coordinates
$k^{a}$
. Using cylindrical polar coordinates
![]() $(r,z)$
with their origin on the substrate at the centre of the droplet, the free surface of the droplet is denoted by
$(r,z)$
with their origin on the substrate at the centre of the droplet, the free surface of the droplet is denoted by
![]() $z=h(r,t)$
, the concentration of vapour in the atmosphere is denoted by
$z=h(r,t)$
, the concentration of vapour in the atmosphere is denoted by
![]() $c=c(r,z,t)$
and the temperatures of the atmosphere, the droplet and the substrate are denoted by
$c=c(r,z,t)$
and the temperatures of the atmosphere, the droplet and the substrate are denoted by
![]() $T^{a}=T^{a}(r,z,t)$
,
$T^{a}=T^{a}(r,z,t)$
,
![]() $T=T(r,z,t)$
and
$T=T(r,z,t)$
and
![]() $T^{s}=T^{s}(r,z,t)$
, respectively. The geometry of the problem is shown in figure 1.
$T^{s}=T^{s}(r,z,t)$
, respectively. The geometry of the problem is shown in figure 1.
The transport of vapour in the atmosphere is due solely to diffusion, and so
![]() $c$
satisfies Laplace’s equation in the appropriate domain. At the free surface of the droplet the atmosphere is saturated with vapour, and so
$c$
satisfies Laplace’s equation in the appropriate domain. At the free surface of the droplet the atmosphere is saturated with vapour, and so
![]() $c$
takes its saturation value, denoted by
$c$
takes its saturation value, denoted by
![]() $c_{sat}=c_{sat}(T)$
, which we assume to be a linearly increasing function of
$c_{sat}=c_{sat}(T)$
, which we assume to be a linearly increasing function of
![]() $T$
given by
$T$
given by
![]() $c_{sat}(T)=c_{sat}(T_{\infty })+c_{sat}^{\prime }(T_{\infty })(T-T_{\infty })$
. (Note that Sefiane et al. (Reference Sefiane, Wilson, David, Dunn and Duffy2009) and Ait Saada et al. (Reference Ait Saada, Chikh and Tadrist2013) considered a nonlinear dependence of
$c_{sat}(T)=c_{sat}(T_{\infty })+c_{sat}^{\prime }(T_{\infty })(T-T_{\infty })$
. (Note that Sefiane et al. (Reference Sefiane, Wilson, David, Dunn and Duffy2009) and Ait Saada et al. (Reference Ait Saada, Chikh and Tadrist2013) considered a nonlinear dependence of
![]() $c_{sat}$
on
$c_{sat}$
on
![]() $T$
.) There is no mass flux through the unwetted part of the substrate, and far from the droplet
$T$
.) There is no mass flux through the unwetted part of the substrate, and far from the droplet
![]() $c$
approaches its ambient value
$c$
approaches its ambient value
![]() $Hc_{sat}(T_{\infty })$
, where
$Hc_{sat}(T_{\infty })$
, where
![]() $H$
$H$
![]() $(0\leqslant H\leqslant 1)$
denotes the relative saturation of the ambient atmosphere. The local evaporative mass flux from the droplet, denoted by
$(0\leqslant H\leqslant 1)$
denotes the relative saturation of the ambient atmosphere. The local evaporative mass flux from the droplet, denoted by
![]() $J=J(r,t)$
, is given by
$J=J(r,t)$
, is given by
![]() $J=-D\unicode[STIX]{x1D735}c\boldsymbol{\cdot }\boldsymbol{n}$
, where
$J=-D\unicode[STIX]{x1D735}c\boldsymbol{\cdot }\boldsymbol{n}$
, where
![]() $D$
is the coefficient of diffusion of vapour in the atmosphere and
$D$
is the coefficient of diffusion of vapour in the atmosphere and
![]() $\boldsymbol{n}$
is the unit outward normal to the free surface of the droplet. The total evaporation rate,
$\boldsymbol{n}$
is the unit outward normal to the free surface of the droplet. The total evaporation rate,
![]() $-\unicode[STIX]{x1D70C}\,\text{d}V/\text{d}t$
, is obtained by integrating
$-\unicode[STIX]{x1D70C}\,\text{d}V/\text{d}t$
, is obtained by integrating
![]() $J$
over the free surface of the droplet.
$J$
over the free surface of the droplet.
Transport of heat in the atmosphere, the droplet and the substrate is due solely to thermal conduction, and so
![]() $T^{a}$
,
$T^{a}$
,
![]() $T$
and
$T$
and
![]() $T^{s}$
also satisfy Laplace’s equation in the appropriate domains. At the free surface of the droplet
$T^{s}$
also satisfy Laplace’s equation in the appropriate domains. At the free surface of the droplet
![]() $J$
satisfies the local energy balance
$J$
satisfies the local energy balance
where
![]() ${\mathcal{L}}$
is the latent heat of vaporisation, while on both the wetted and unwetted parts of the substrate both the temperature and the heat flux are continuous, and far from the droplet
${\mathcal{L}}$
is the latent heat of vaporisation, while on both the wetted and unwetted parts of the substrate both the temperature and the heat flux are continuous, and far from the droplet
![]() $T^{a}$
approaches its ambient value
$T^{a}$
approaches its ambient value
![]() $T_{\infty }$
. Note that if we were simply to set
$T_{\infty }$
. Note that if we were simply to set
![]() $T^{a}\equiv T_{\infty }$
(which does not, in general, satisfy the conditions of continuity of heat flux on the unwetted part of the substrate or of continuity of temperature on the free surface of the droplet) we would recover the extended model proposed by Dunn et al. (Reference Dunn, Wilson, Duffy, David and Sefiane2009a
). However, as described below, in the present work we exploit the fact that in practice the atmosphere is typically a relatively poor thermal conductor to obtain a more physically realistic extended model.
$T^{a}\equiv T_{\infty }$
(which does not, in general, satisfy the conditions of continuity of heat flux on the unwetted part of the substrate or of continuity of temperature on the free surface of the droplet) we would recover the extended model proposed by Dunn et al. (Reference Dunn, Wilson, Duffy, David and Sefiane2009a
). However, as described below, in the present work we exploit the fact that in practice the atmosphere is typically a relatively poor thermal conductor to obtain a more physically realistic extended model.
In order to make analytical progress we follow Dunn et al. (Reference Dunn, Wilson, Duffy, David and Sefiane2008, Reference Dunn, Wilson, Duffy and Sefiane2009b
) and assume that both the droplet and the substrate are thin (i.e. that
![]() $\unicode[STIX]{x1D703}(0)\ll 1$
and
$\unicode[STIX]{x1D703}(0)\ll 1$
and
![]() $h^{s}/R(0)\ll 1$
), but make no assumption about their relative thicknesses (i.e. we make no a priori assumption about the size of
$h^{s}/R(0)\ll 1$
), but make no assumption about their relative thicknesses (i.e. we make no a priori assumption about the size of
![]() $h^{s}/(\unicode[STIX]{x1D703}(0)R(0))$
). Hence at leading order in the appropriate thin-film limit, the free surface of the droplet is given by
$h^{s}/(\unicode[STIX]{x1D703}(0)R(0))$
). Hence at leading order in the appropriate thin-film limit, the free surface of the droplet is given by
![]() $h=\unicode[STIX]{x1D703}(R^{2}-r^{2})/(2R)$
and the volume of the droplet is given by
$h=\unicode[STIX]{x1D703}(R^{2}-r^{2})/(2R)$
and the volume of the droplet is given by
![]() $V=\unicode[STIX]{x03C0}\unicode[STIX]{x1D703}R^{3}/4$
.
$V=\unicode[STIX]{x03C0}\unicode[STIX]{x1D703}R^{3}/4$
.
We non-dimensionalise and scale
![]() $r$
with
$r$
with
![]() $R(0)$
,
$R(0)$
,
![]() $z$
in the droplet with
$z$
in the droplet with
![]() $\unicode[STIX]{x1D703}(0)R(0)$
,
$\unicode[STIX]{x1D703}(0)R(0)$
,
![]() $z$
in the substrate with
$z$
in the substrate with
![]() $h^{s}$
,
$h^{s}$
,
![]() $z$
in the atmosphere with
$z$
in the atmosphere with
![]() $R(0)$
,
$R(0)$
,
![]() $h$
with
$h$
with
![]() $\unicode[STIX]{x1D703}(0)R(0)$
,
$\unicode[STIX]{x1D703}(0)R(0)$
,
![]() $V$
with
$V$
with
![]() $\unicode[STIX]{x1D703}(0)R(0)^{3}$
,
$\unicode[STIX]{x1D703}(0)R(0)^{3}$
,
![]() $\unicode[STIX]{x1D703}$
with
$\unicode[STIX]{x1D703}$
with
![]() $\unicode[STIX]{x1D703}(0)$
,
$\unicode[STIX]{x1D703}(0)$
,
![]() $T^{a}$
,
$T^{a}$
,
![]() $T$
and
$T$
and
![]() $T^{s}$
with
$T^{s}$
with
![]() $T_{\infty }$
,
$T_{\infty }$
,
![]() $c-Hc_{sat}(T_{\infty })$
with
$c-Hc_{sat}(T_{\infty })$
with
![]() $(1-H)c_{sat}(T_{\infty })$
,
$(1-H)c_{sat}(T_{\infty })$
,
![]() $J$
with
$J$
with
![]() $D(1-H)c_{sat}(T_{\infty })/R(0)$
and
$D(1-H)c_{sat}(T_{\infty })/R(0)$
and
![]() $t$
with the characteristic time scale for the evaporation of a thin droplet according to the basic model, namely
$t$
with the characteristic time scale for the evaporation of a thin droplet according to the basic model, namely
In practice, the atmosphere is typically a relatively poor thermal conductor, and provided that
the problem for
![]() $T^{a}$
decouples from that for
$T^{a}$
decouples from that for
![]() $T$
,
$T$
,
![]() $T^{s}$
and
$T^{s}$
and
![]() $c$
. Note that, since both the droplet and the substrate are thin, these conditions hold when
$c$
. Note that, since both the droplet and the substrate are thin, these conditions hold when
![]() $k$
and
$k$
and
![]() $k^{s}$
are comparable with
$k^{s}$
are comparable with
![]() $k^{a}$
. When (2.3) holds it is straightforward to show that
$k^{a}$
. When (2.3) holds it is straightforward to show that
![]() $T$
and
$T$
and
![]() $T^{s}$
are given by
$T^{s}$
are given by
that
![]() $c$
satisfies
$c$
satisfies
subject to
and
and that
![]() $T^{a}$
satisfies
$T^{a}$
satisfies
subject to
and
The total evaporation rate is then given by
where
and
are non-dimensional measures of the variation of the saturation concentration of the vapour with temperature, the relative thermal resistance of the droplet and the substrate and the evaporative cooling, respectively. Whereas (2.7)–(2.10) show that the solution for
![]() $c$
, and hence the evolution of the droplet given by (2.15) and (2.16), depends on
$c$
, and hence the evolution of the droplet given by (2.15) and (2.16), depends on
![]() $\unicode[STIX]{x0394}C$
and
$\unicode[STIX]{x0394}C$
and
![]() $S$
but not
$S$
but not
![]() $E$
, (2.4)–(2.6) and (2.11)–(2.14) show that the evaporative cooling of the atmosphere, the droplet and the substrate also depends on
$E$
, (2.4)–(2.6) and (2.11)–(2.14) show that the evaporative cooling of the atmosphere, the droplet and the substrate also depends on
![]() $E$
.
$E$
.
Note that although, as we have already mentioned, the present extended model differs from that proposed by Dunn et al. (Reference Dunn, Wilson, Duffy, David and Sefiane2009a
), in the present limit of a thin droplet on a thin substrate the problem for
![]() $T$
,
$T$
,
![]() $T^{s}$
and
$T^{s}$
and
![]() $c$
given by (2.4)–(2.10), but not, of course, that for
$c$
given by (2.4)–(2.10), but not, of course, that for
![]() $T^{a}$
given by (2.11)–(2.14), coincides exactly with that analysed by Dunn et al. (Reference Dunn, Wilson, Duffy, David and Sefiane2008, Reference Dunn, Wilson, Duffy and Sefiane2009b
). However, these latter authors considered only the initial evolution of a pinned droplet (i.e. evolution of a droplet evaporating in the CR mode for
$T^{a}$
given by (2.11)–(2.14), coincides exactly with that analysed by Dunn et al. (Reference Dunn, Wilson, Duffy, David and Sefiane2008, Reference Dunn, Wilson, Duffy and Sefiane2009b
). However, these latter authors considered only the initial evolution of a pinned droplet (i.e. evolution of a droplet evaporating in the CR mode for
![]() $t=O(1)$
) and did not analyse either the entire evolution of the droplet or consider other modes of evaporation, both of which we do in the present work.
$t=O(1)$
) and did not analyse either the entire evolution of the droplet or consider other modes of evaporation, both of which we do in the present work.
In the special case
![]() $\unicode[STIX]{x0394}C=0$
in which
$\unicode[STIX]{x0394}C=0$
in which
![]() $c_{sat}$
is independent of
$c_{sat}$
is independent of
![]() $T$
the concentration of vapour at the free surface of the droplet is constant and we recover the basic model in which the solution for
$T$
the concentration of vapour at the free surface of the droplet is constant and we recover the basic model in which the solution for
![]() $c$
, and hence the evolution of the droplet, is also independent of
$c$
, and hence the evolution of the droplet, is also independent of
![]() $S$
, i.e. is entirely independent of the thermal properties of the system. Explicit expressions for the lifetimes of thin droplets in this special case (albeit using a different non-dimensionalisation of time) were obtained by Stauber et al. (Reference Stauber, Wilson, Duffy and Sefiane2014) for the CR, CA and SS modes, and by Stauber (Reference Stauber2015) for the SJ mode. For brevity, these expressions are not reproduced here, but the key observation is that when
$S$
, i.e. is entirely independent of the thermal properties of the system. Explicit expressions for the lifetimes of thin droplets in this special case (albeit using a different non-dimensionalisation of time) were obtained by Stauber et al. (Reference Stauber, Wilson, Duffy and Sefiane2014) for the CR, CA and SS modes, and by Stauber (Reference Stauber2015) for the SJ mode. For brevity, these expressions are not reproduced here, but the key observation is that when
![]() $\unicode[STIX]{x0394}C=0$
the lifetimes of thin droplets are, as anticipated, of the order of the basic time scale (2.2). This time scale is also applicable when thermal effects are weak, but not, as we shall show in the present work, when they are strong.
$\unicode[STIX]{x0394}C=0$
the lifetimes of thin droplets are, as anticipated, of the order of the basic time scale (2.2). This time scale is also applicable when thermal effects are weak, but not, as we shall show in the present work, when they are strong.
3 When the substrate has a high thermal resistance
Consider the evolution of an evaporating droplet using the extended model described in § 2 when the substrate has a high thermal resistance relative to the droplet (i.e. when the substrate is highly insulating and/or thick relative to the droplet), corresponding to the asymptotic limit
![]() $S\rightarrow \infty$
with
$S\rightarrow \infty$
with
![]() $\unicode[STIX]{x0394}C\neq 0$
.
$\unicode[STIX]{x0394}C\neq 0$
.
Inspection of (2.7)–(2.15) suggests that in the limit
![]() $S\rightarrow \infty$
the complete evolution of a droplet will occur over the long time scale
$S\rightarrow \infty$
the complete evolution of a droplet will occur over the long time scale
![]() $t=O(S)\gg 1$
. In order to obtain a uniformly valid leading-order asymptotic solution able to capture the complete evolution of the droplet we therefore rescale
$t=O(S)\gg 1$
. In order to obtain a uniformly valid leading-order asymptotic solution able to capture the complete evolution of the droplet we therefore rescale
![]() $c$
and
$c$
and
![]() $J$
with
$J$
with
![]() $1/S$
and
$1/S$
and
![]() $t$
with
$t$
with
![]() $S$
by writing
$S$
by writing
![]() $c=\tilde{c}/S$
,
$c=\tilde{c}/S$
,
![]() $J=\tilde{J}/S$
and
$J=\tilde{J}/S$
and
![]() $t=S\tilde{t}$
, and seek an asymptotic expansion for
$t=S\tilde{t}$
, and seek an asymptotic expansion for
![]() $\tilde{c}$
in the form
$\tilde{c}$
in the form
![]() $\tilde{c}(r,z,\tilde{t})=\tilde{c}_{0}(r,z,\tilde{t})+O(1/S)$
with corresponding asymptotic expansions for the other dependent variables.
$\tilde{c}(r,z,\tilde{t})=\tilde{c}_{0}(r,z,\tilde{t})+O(1/S)$
with corresponding asymptotic expansions for the other dependent variables.
At leading order in the limit
![]() $S\rightarrow \infty$
we obtain
$S\rightarrow \infty$
we obtain
![]() $\tilde{J}_{0}=1/\unicode[STIX]{x0394}C$
(i.e. at leading order the mass flux from the free surface of the droplet is uniform and constant),
$\tilde{J}_{0}=1/\unicode[STIX]{x0394}C$
(i.e. at leading order the mass flux from the free surface of the droplet is uniform and constant),
![]() $T_{0}=1-E/\unicode[STIX]{x0394}C$
(i.e. at leading order the droplet is uniformly cooled by a constant amount
$T_{0}=1-E/\unicode[STIX]{x0394}C$
(i.e. at leading order the droplet is uniformly cooled by a constant amount
![]() $E/\unicode[STIX]{x0394}C$
) and
$E/\unicode[STIX]{x0394}C$
) and
![]() $T_{0}^{s}=1-E(z+1)/\unicode[STIX]{x0394}C$
and hence (2.15) yields the equation describing the leading-order evolution of the droplet, namely
$T_{0}^{s}=1-E(z+1)/\unicode[STIX]{x0394}C$
and hence (2.15) yields the equation describing the leading-order evolution of the droplet, namely
An explicit expression for the leading-order concentration of vapour,
![]() $\tilde{c}_{0}$
, can be obtained (see, for example, Mehta & Bose Reference Mehta and Bose1983), but, since this is not required in order to determine the leading-order evolution of the droplet, it is not reproduced here for brevity.
$\tilde{c}_{0}$
, can be obtained (see, for example, Mehta & Bose Reference Mehta and Bose1983), but, since this is not required in order to determine the leading-order evolution of the droplet, it is not reproduced here for brevity.
3.1 Evolution of a droplet evaporating in the constant radius mode
For a droplet evaporating in the CR mode with
![]() $R_{0}\equiv 1$
, solving (3.1) yields
$R_{0}\equiv 1$
, solving (3.1) yields
and hence the lifetime of the droplet, denoted by
![]() $\tilde{t}_{CR}$
, is given by
$\tilde{t}_{CR}$
, is given by
![]() $\tilde{t}_{CR}=\unicode[STIX]{x0394}C/4$
.
$\tilde{t}_{CR}=\unicode[STIX]{x0394}C/4$
.
3.2 Evolution of a droplet evaporating in the constant angle mode
For a droplet evaporating in the CA mode with
![]() $\unicode[STIX]{x1D703}_{0}\equiv 1$
, solving (3.1) yields
$\unicode[STIX]{x1D703}_{0}\equiv 1$
, solving (3.1) yields
and hence the lifetime of the droplet, denoted by
![]() $\tilde{t}_{CA}$
, is given by
$\tilde{t}_{CA}$
, is given by
![]() $\tilde{t}_{CA}=3\unicode[STIX]{x0394}C/4=3\tilde{t}_{CR}$
.
$\tilde{t}_{CA}=3\unicode[STIX]{x0394}C/4=3\tilde{t}_{CR}$
.
Both
![]() $\tilde{t}_{CR}$
and
$\tilde{t}_{CR}$
and
![]() $\tilde{t}_{CA}$
are directly proportional to
$\tilde{t}_{CA}$
are directly proportional to
![]() $\unicode[STIX]{x0394}C$
(i.e. stronger variation of
$\unicode[STIX]{x0394}C$
(i.e. stronger variation of
![]() $c_{sat}$
with
$c_{sat}$
with
![]() $T$
leads to slower evaporation and hence to longer lifetimes), and their ratio is exactly 3. This latter result contrasts with that in the special case
$T$
leads to slower evaporation and hence to longer lifetimes), and their ratio is exactly 3. This latter result contrasts with that in the special case
![]() $\unicode[STIX]{x0394}C=0$
discussed by Stauber et al. (Reference Stauber, Wilson, Duffy and Sefiane2014) for which the corresponding ratio is exactly
$\unicode[STIX]{x0394}C=0$
discussed by Stauber et al. (Reference Stauber, Wilson, Duffy and Sefiane2014) for which the corresponding ratio is exactly
![]() $3/2$
.
$3/2$
.
3.3 Evolution of a droplet evaporating in the stick–slide mode
The stick–slide (SS) mode of evaporation consists of a CR phase which lasts until the contact angle reaches a critical receding contact angle
![]() $\unicode[STIX]{x1D703}^{\star }$
(
$\unicode[STIX]{x1D703}^{\star }$
(
![]() $0\leqslant \unicode[STIX]{x1D703}^{\star }\leqslant 1$
) followed by a CA phase. For a droplet evaporating in this mode, solving (3.1) yields (3.2) for
$0\leqslant \unicode[STIX]{x1D703}^{\star }\leqslant 1$
) followed by a CA phase. For a droplet evaporating in this mode, solving (3.1) yields (3.2) for
![]() $0<\tilde{t}<\tilde{t}^{\star }$
and
$0<\tilde{t}<\tilde{t}^{\star }$
and
for
![]() $\tilde{t}^{\star }<\tilde{t}<\tilde{t}_{SS}$
, where
$\tilde{t}^{\star }<\tilde{t}<\tilde{t}_{SS}$
, where
are the depinning time (i.e. the time at which the contact angle
![]() $\unicode[STIX]{x1D703}_{0}$
reaches the critical receding angle
$\unicode[STIX]{x1D703}_{0}$
reaches the critical receding angle
![]() $\unicode[STIX]{x1D703}^{\star }$
) and the lifetime of the droplet, respectively. Both
$\unicode[STIX]{x1D703}^{\star }$
) and the lifetime of the droplet, respectively. Both
![]() $\tilde{t}^{\star }$
and
$\tilde{t}^{\star }$
and
![]() $\tilde{t}_{SS}$
are directly proportional to
$\tilde{t}_{SS}$
are directly proportional to
![]() $\unicode[STIX]{x0394}C$
,
$\unicode[STIX]{x0394}C$
,
![]() $\tilde{t}^{\star }$
is a linearly decreasing function of
$\tilde{t}^{\star }$
is a linearly decreasing function of
![]() $\unicode[STIX]{x1D703}^{\star }$
satisfying
$\unicode[STIX]{x1D703}^{\star }$
satisfying
![]() $\tilde{t}^{\star }=\tilde{t}_{CR}$
at
$\tilde{t}^{\star }=\tilde{t}_{CR}$
at
![]() $\unicode[STIX]{x1D703}^{\star }=0$
and
$\unicode[STIX]{x1D703}^{\star }=0$
and
![]() $\tilde{t}^{\star }=0$
at
$\tilde{t}^{\star }=0$
at
![]() $\unicode[STIX]{x1D703}^{\star }=1$
, and
$\unicode[STIX]{x1D703}^{\star }=1$
, and
![]() $\tilde{t}_{SS}$
is a linearly increasing function of
$\tilde{t}_{SS}$
is a linearly increasing function of
![]() $\unicode[STIX]{x1D703}^{\star }$
satisfying
$\unicode[STIX]{x1D703}^{\star }$
satisfying
![]() $\tilde{t}_{SS}=\tilde{t}_{CR}$
at
$\tilde{t}_{SS}=\tilde{t}_{CR}$
at
![]() $\unicode[STIX]{x1D703}^{\star }=0$
and
$\unicode[STIX]{x1D703}^{\star }=0$
and
![]() $\tilde{t}_{SS}=\tilde{t}_{CA}$
at
$\tilde{t}_{SS}=\tilde{t}_{CA}$
at
![]() $\unicode[STIX]{x1D703}^{\star }=1$
.
$\unicode[STIX]{x1D703}^{\star }=1$
.
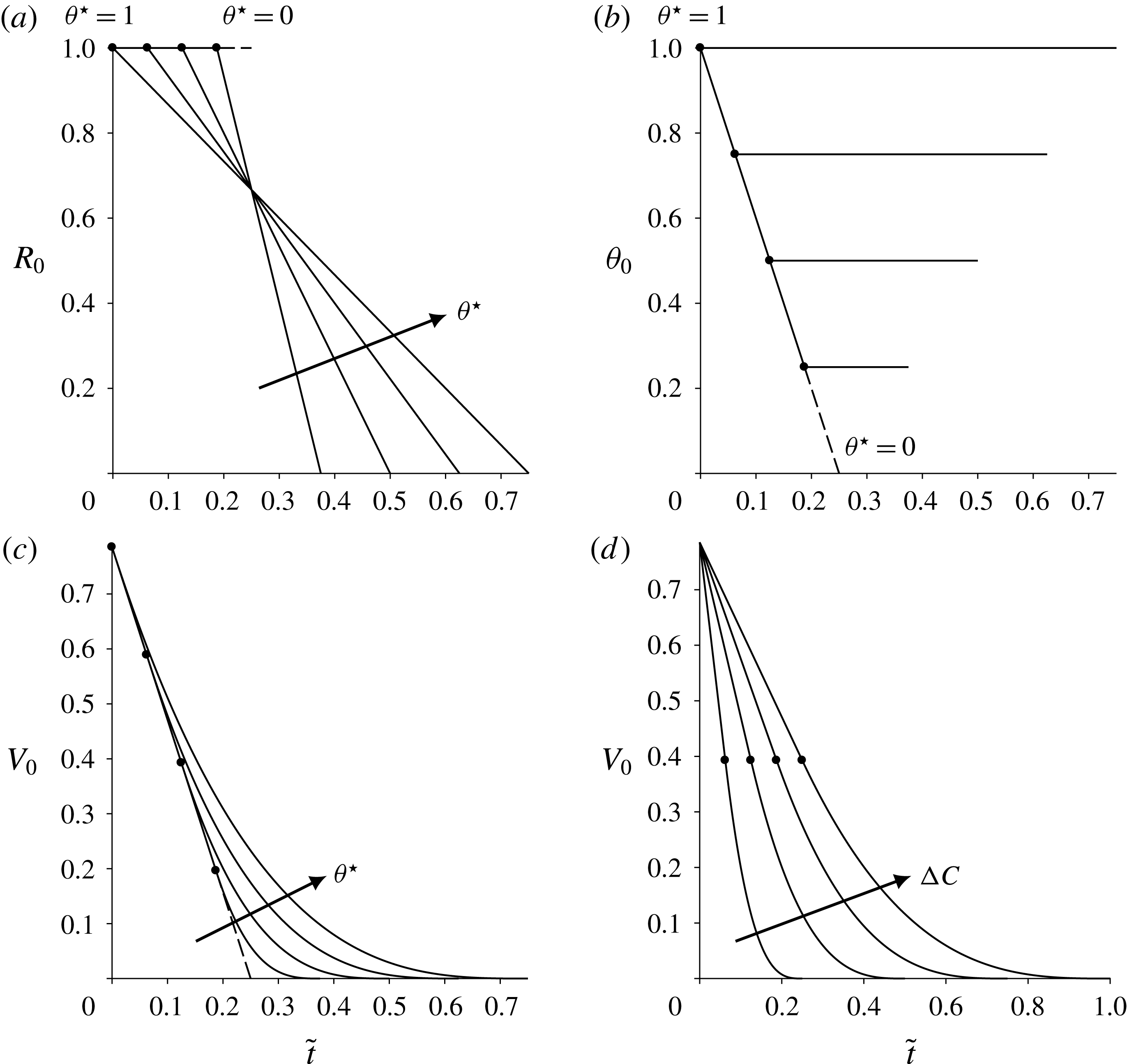
Figure 2. Evolution of a droplet on a substrate with a high thermal resistance (i.e. in the limit
![]() $S\rightarrow \infty$
with
$S\rightarrow \infty$
with
![]() $\unicode[STIX]{x0394}C\neq 0$
) evaporating in the SS mode. Plots of (a)
$\unicode[STIX]{x0394}C\neq 0$
) evaporating in the SS mode. Plots of (a)
![]() $R_{0}$
, (b)
$R_{0}$
, (b)
![]() $\unicode[STIX]{x1D703}_{0}$
and (c)
$\unicode[STIX]{x1D703}_{0}$
and (c)
![]() $V_{0}$
as functions of
$V_{0}$
as functions of
![]() $\tilde{t}$
for
$\tilde{t}$
for
![]() $\unicode[STIX]{x1D703}^{\star }=0$
(i.e. the CR mode, shown dashed),
$\unicode[STIX]{x1D703}^{\star }=0$
(i.e. the CR mode, shown dashed),
![]() $1/4$
,
$1/4$
,
![]() $1/2$
,
$1/2$
,
![]() $3/4$
and 1 (i.e. the CA mode) with
$3/4$
and 1 (i.e. the CA mode) with
![]() $\unicode[STIX]{x0394}C=1$
, and (d)
$\unicode[STIX]{x0394}C=1$
, and (d)
![]() $V_{0}$
as a function of
$V_{0}$
as a function of
![]() $\tilde{t}$
for
$\tilde{t}$
for
![]() $\unicode[STIX]{x0394}C=1/2$
, 1,
$\unicode[STIX]{x0394}C=1/2$
, 1,
![]() $3/2$
and 2 with
$3/2$
and 2 with
![]() $\unicode[STIX]{x1D703}^{\star }=1/2$
. The dots (
$\unicode[STIX]{x1D703}^{\star }=1/2$
. The dots (
![]() $\bullet$
) denote the instants at which depinning occurs (i.e.
$\bullet$
) denote the instants at which depinning occurs (i.e.
![]() $\tilde{t}=\tilde{t}^{\star }$
), and in (a), (c) and (d) the arrows indicate the direction of increasing values of the appropriate parameter.
$\tilde{t}=\tilde{t}^{\star }$
), and in (a), (c) and (d) the arrows indicate the direction of increasing values of the appropriate parameter.
Figure 2 shows (a)
![]() $R_{0}$
, (b)
$R_{0}$
, (b)
![]() $\unicode[STIX]{x1D703}_{0}$
and (c)
$\unicode[STIX]{x1D703}_{0}$
and (c)
![]() $V_{0}$
as functions of
$V_{0}$
as functions of
![]() $\tilde{t}$
for various values of
$\tilde{t}$
for various values of
![]() $\unicode[STIX]{x1D703}^{\star }$
, including
$\unicode[STIX]{x1D703}^{\star }$
, including
![]() $\unicode[STIX]{x1D703}^{\star }=0$
(i.e. the CR mode given by (3.2)) and
$\unicode[STIX]{x1D703}^{\star }=0$
(i.e. the CR mode given by (3.2)) and
![]() $\unicode[STIX]{x1D703}^{\star }=1$
(i.e. the CA mode given by (3.3)), and (d)
$\unicode[STIX]{x1D703}^{\star }=1$
(i.e. the CA mode given by (3.3)), and (d)
![]() $V_{0}$
as a function of
$V_{0}$
as a function of
![]() $\tilde{t}$
for various values of
$\tilde{t}$
for various values of
![]() $\unicode[STIX]{x0394}C$
. Figure 2 illustrates that
$\unicode[STIX]{x0394}C$
. Figure 2 illustrates that
![]() $R_{0}$
and
$R_{0}$
and
![]() $\unicode[STIX]{x1D703}_{0}$
are either constant or linearly decreasing functions of
$\unicode[STIX]{x1D703}_{0}$
are either constant or linearly decreasing functions of
![]() $\tilde{t}$
,
$\tilde{t}$
,
![]() $V_{0}$
is first (for
$V_{0}$
is first (for
![]() $0<\tilde{t}<\tilde{t}^{\star }$
) a linearly and then (for
$0<\tilde{t}<\tilde{t}^{\star }$
) a linearly and then (for
![]() $\tilde{t}^{\star }<\tilde{t}<\tilde{t}_{SS}$
) a cubically decreasing function of
$\tilde{t}^{\star }<\tilde{t}<\tilde{t}_{SS}$
) a cubically decreasing function of
![]() $\tilde{t}$
, and as
$\tilde{t}$
, and as
![]() $\unicode[STIX]{x1D703}^{\star }$
increases the droplet depins earlier but has a longer lifetime. Somewhat more unexpectedly, figure 2(a) also illustrates that, except in the special case
$\unicode[STIX]{x1D703}^{\star }$
increases the droplet depins earlier but has a longer lifetime. Somewhat more unexpectedly, figure 2(a) also illustrates that, except in the special case
![]() $\unicode[STIX]{x1D703}^{\star }=0$
,
$\unicode[STIX]{x1D703}^{\star }=0$
,
![]() $R_{0}=2/3$
at
$R_{0}=2/3$
at
![]() $\tilde{t}=\tilde{t}_{CR}$
irrespective of the value of the critical receding angle
$\tilde{t}=\tilde{t}_{CR}$
irrespective of the value of the critical receding angle
![]() $\unicode[STIX]{x1D703}^{\star }$
(i.e. whatever the non-zero value of
$\unicode[STIX]{x1D703}^{\star }$
(i.e. whatever the non-zero value of
![]() $\unicode[STIX]{x1D703}^{\star }$
, the contact radius always reduces to
$\unicode[STIX]{x1D703}^{\star }$
, the contact radius always reduces to
![]() $2/3$
of its initial value at
$2/3$
of its initial value at
![]() $\tilde{t}=\tilde{t}_{CR}$
).
$\tilde{t}=\tilde{t}_{CR}$
).
3.4 Evolution of a droplet evaporating in the stick–jump mode
The stick–jump (SJ) mode of evaporation consists of an infinite series of stick (i.e. CR) phases separated by an infinite series of jump phases in which the contact angle jumps instantaneously from a minimum value
![]() $\unicode[STIX]{x1D703}_{min}$
to a maximum value
$\unicode[STIX]{x1D703}_{min}$
to a maximum value
![]() $\unicode[STIX]{x1D703}_{max}$
(
$\unicode[STIX]{x1D703}_{max}$
(
![]() $0\leqslant \unicode[STIX]{x1D703}_{min}\leqslant \unicode[STIX]{x1D703}_{max}\leqslant 1$
) with a corresponding instantaneous jump in the contact radius. For a droplet evaporating in this mode, if we denote by
$0\leqslant \unicode[STIX]{x1D703}_{min}\leqslant \unicode[STIX]{x1D703}_{max}\leqslant 1$
) with a corresponding instantaneous jump in the contact radius. For a droplet evaporating in this mode, if we denote by
![]() $R_{n}$
(
$R_{n}$
(
![]() $n=1,2,3,\ldots$
) the constant value of
$n=1,2,3,\ldots$
) the constant value of
![]() $R_{0}$
during the
$R_{0}$
during the
![]() $n$
th stick (i.e. CR) phase lasting from
$n$
th stick (i.e. CR) phase lasting from
![]() $\tilde{t}=\tilde{t}_{n-1}$
to
$\tilde{t}=\tilde{t}_{n-1}$
to
![]() $\tilde{t}=\tilde{t}_{n}$
, then, by conservation of mass during the
$\tilde{t}=\tilde{t}_{n}$
, then, by conservation of mass during the
![]() $n$
th jump phase occurring at
$n$
th jump phase occurring at
![]() $\tilde{t}=\tilde{t}_{n}$
(
$\tilde{t}=\tilde{t}_{n}$
(
![]() $n=1,2,3,\ldots$
), we have
$n=1,2,3,\ldots$
), we have
![]() $\unicode[STIX]{x1D703}_{min}R_{n}^{3}=\unicode[STIX]{x1D703}_{max}R_{n+1}^{3}$
, and so
$\unicode[STIX]{x1D703}_{min}R_{n}^{3}=\unicode[STIX]{x1D703}_{max}R_{n+1}^{3}$
, and so
During the first stick phase with
![]() $R_{0}=R_{1}\equiv 1$
from
$R_{0}=R_{1}\equiv 1$
from
![]() $\tilde{t}=\tilde{t}_{0}=0$
to
$\tilde{t}=\tilde{t}_{0}=0$
to
![]() $\tilde{t}=\tilde{t}_{1}=\unicode[STIX]{x0394}C(1-\unicode[STIX]{x1D703}_{min})/4$
,
$\tilde{t}=\tilde{t}_{1}=\unicode[STIX]{x0394}C(1-\unicode[STIX]{x1D703}_{min})/4$
,
![]() $\unicode[STIX]{x1D703}_{0}$
and
$\unicode[STIX]{x1D703}_{0}$
and
![]() $V_{0}$
are given by (3.2), and thereafter during the
$V_{0}$
are given by (3.2), and thereafter during the
![]() $n$
th stick phase (
$n$
th stick phase (
![]() $n=2,3,4,\ldots$
) with
$n=2,3,4,\ldots$
) with
![]() $R_{0}=R_{n}$
from
$R_{0}=R_{n}$
from
![]() $\tilde{t}=\tilde{t}_{n-1}$
to
$\tilde{t}=\tilde{t}_{n-1}$
to
![]() $\tilde{t}=\tilde{t}_{n}$
,
$\tilde{t}=\tilde{t}_{n}$
,
where
Taking the limit
![]() $n\rightarrow \infty$
in (3.8) we obtain the lifetime of the droplet, namely
$n\rightarrow \infty$
in (3.8) we obtain the lifetime of the droplet, namely
In particular,
![]() $\tilde{t}_{SJ}$
is directly proportional to
$\tilde{t}_{SJ}$
is directly proportional to
![]() $\unicode[STIX]{x0394}C$
, and is an increasing function of both
$\unicode[STIX]{x0394}C$
, and is an increasing function of both
![]() $\unicode[STIX]{x1D703}_{max}$
and
$\unicode[STIX]{x1D703}_{max}$
and
![]() $\unicode[STIX]{x1D703}_{min}\,({<}\unicode[STIX]{x1D703}_{max})$
satisfying
$\unicode[STIX]{x1D703}_{min}\,({<}\unicode[STIX]{x1D703}_{max})$
satisfying
![]() $\tilde{t}_{SJ}=\tilde{t}_{CR}$
when
$\tilde{t}_{SJ}=\tilde{t}_{CR}$
when
![]() $\unicode[STIX]{x1D703}_{max}=0$
and when
$\unicode[STIX]{x1D703}_{max}=0$
and when
![]() $\unicode[STIX]{x1D703}_{min}=0$
, and
$\unicode[STIX]{x1D703}_{min}=0$
, and
![]() $\tilde{t}_{SJ}\rightarrow \tilde{t}_{SS}$
when
$\tilde{t}_{SJ}\rightarrow \tilde{t}_{SS}$
when
![]() $\unicode[STIX]{x1D703}_{max}\rightarrow \unicode[STIX]{x1D703}_{min}=\unicode[STIX]{x1D703}^{\star }$
.
$\unicode[STIX]{x1D703}_{max}\rightarrow \unicode[STIX]{x1D703}_{min}=\unicode[STIX]{x1D703}^{\star }$
.
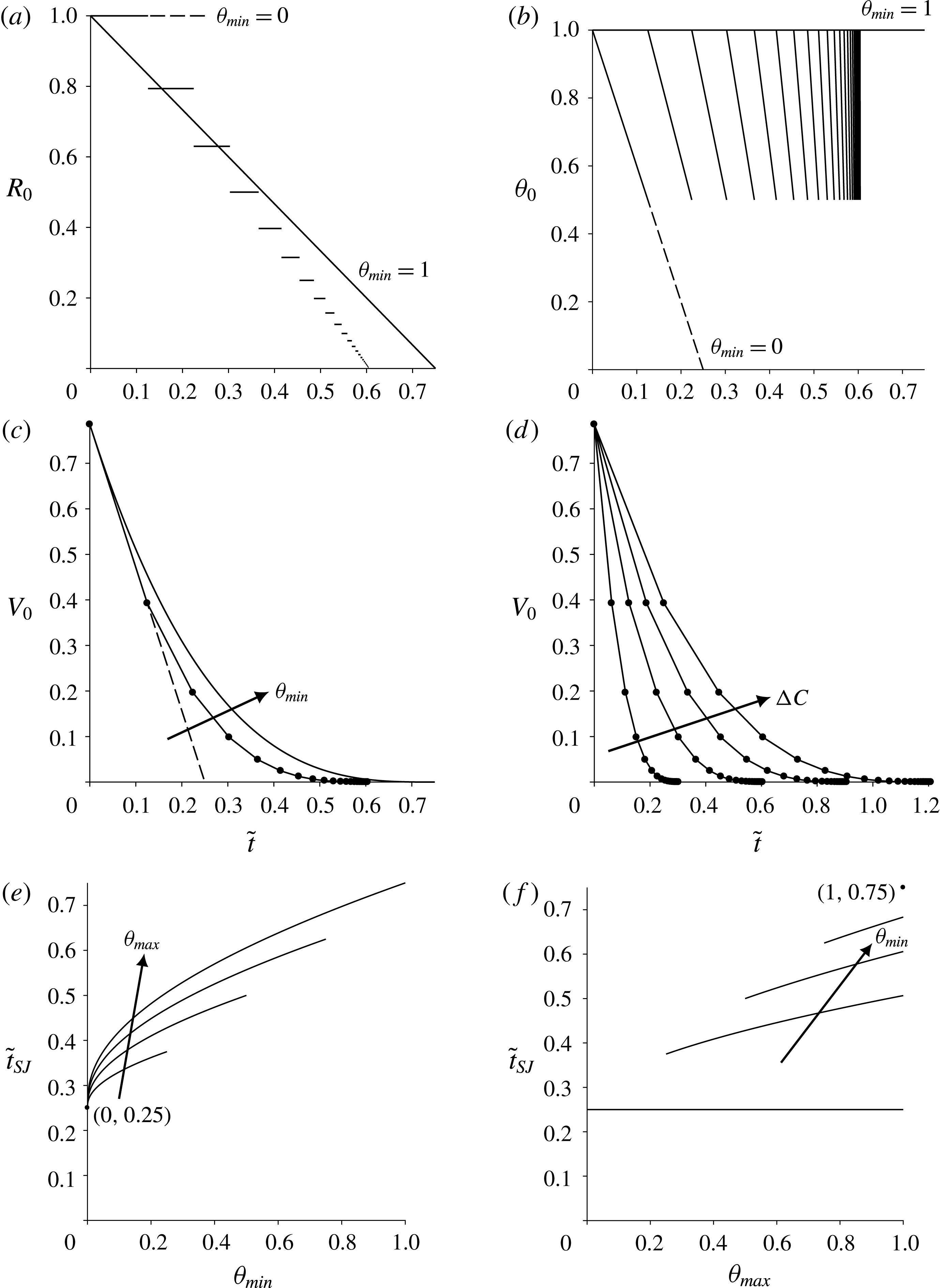
Figure 3. Evolution of a droplet on a substrate with a high thermal resistance (i.e. in the limit
![]() $S\rightarrow \infty$
with
$S\rightarrow \infty$
with
![]() $\unicode[STIX]{x0394}C\neq 0$
) evaporating in the SJ mode. Plots of (a)
$\unicode[STIX]{x0394}C\neq 0$
) evaporating in the SJ mode. Plots of (a)
![]() $R_{0}$
, (b)
$R_{0}$
, (b)
![]() $\unicode[STIX]{x1D703}_{0}$
and (c)
$\unicode[STIX]{x1D703}_{0}$
and (c)
![]() $V_{0}$
as functions of
$V_{0}$
as functions of
![]() $\tilde{t}$
for
$\tilde{t}$
for
![]() $\unicode[STIX]{x1D703}_{min}=0$
(i.e. the CR mode, shown dashed),
$\unicode[STIX]{x1D703}_{min}=0$
(i.e. the CR mode, shown dashed),
![]() $1/2$
and 1 (i.e. the CA mode) with
$1/2$
and 1 (i.e. the CA mode) with
![]() $\unicode[STIX]{x1D703}_{max}=1$
and
$\unicode[STIX]{x1D703}_{max}=1$
and
![]() $\unicode[STIX]{x0394}C=1$
, (d)
$\unicode[STIX]{x0394}C=1$
, (d)
![]() $V_{0}$
as a function of
$V_{0}$
as a function of
![]() $\tilde{t}$
for
$\tilde{t}$
for
![]() $\unicode[STIX]{x0394}C=1/2$
, 1,
$\unicode[STIX]{x0394}C=1/2$
, 1,
![]() $3/2$
and 2 with
$3/2$
and 2 with
![]() $\unicode[STIX]{x1D703}_{max}=1$
and
$\unicode[STIX]{x1D703}_{max}=1$
and
![]() $\unicode[STIX]{x1D703}_{min}=1/2$
, (e)
$\unicode[STIX]{x1D703}_{min}=1/2$
, (e)
![]() $\tilde{t}_{SJ}$
as a function of
$\tilde{t}_{SJ}$
as a function of
![]() $\unicode[STIX]{x1D703}_{min}\,({\leqslant}\unicode[STIX]{x1D703}_{max})$
for
$\unicode[STIX]{x1D703}_{min}\,({\leqslant}\unicode[STIX]{x1D703}_{max})$
for
![]() $\unicode[STIX]{x1D703}_{max}=0$
(i.e. the CR mode),
$\unicode[STIX]{x1D703}_{max}=0$
(i.e. the CR mode),
![]() $1/4$
,
$1/4$
,
![]() $1/2$
,
$1/2$
,
![]() $3/4$
and
$3/4$
and
![]() $1$
, and (f)
$1$
, and (f)
![]() $\tilde{t}_{SJ}$
as a function of
$\tilde{t}_{SJ}$
as a function of
![]() $\unicode[STIX]{x1D703}_{max}\,({\geqslant}\unicode[STIX]{x1D703}_{min})$
for
$\unicode[STIX]{x1D703}_{max}\,({\geqslant}\unicode[STIX]{x1D703}_{min})$
for
![]() $\unicode[STIX]{x1D703}_{min}=0$
(i.e. the CR mode),
$\unicode[STIX]{x1D703}_{min}=0$
(i.e. the CR mode),
![]() $1/4$
,
$1/4$
,
![]() $1/2$
,
$1/2$
,
![]() $3/4$
and
$3/4$
and
![]() $1$
(i.e. the CA mode), with
$1$
(i.e. the CA mode), with
![]() $\unicode[STIX]{x0394}C=1$
. In (c) and (d) the dots (
$\unicode[STIX]{x0394}C=1$
. In (c) and (d) the dots (
![]() $\bullet$
) denote the instants at which the jump phases occur (i.e.
$\bullet$
) denote the instants at which the jump phases occur (i.e.
![]() $\tilde{t}=\tilde{t}_{n}$
for
$\tilde{t}=\tilde{t}_{n}$
for
![]() $n=1,2,3,\ldots$
), and in (c)–(f) the arrows indicate the direction of increasing values of the appropriate parameter.
$n=1,2,3,\ldots$
), and in (c)–(f) the arrows indicate the direction of increasing values of the appropriate parameter.
Figure 3 shows (a)
![]() $R_{0}$
, (b)
$R_{0}$
, (b)
![]() $\unicode[STIX]{x1D703}_{0}$
and (c)
$\unicode[STIX]{x1D703}_{0}$
and (c)
![]() $V_{0}$
as functions of
$V_{0}$
as functions of
![]() $\tilde{t}$
for various values of
$\tilde{t}$
for various values of
![]() $\unicode[STIX]{x1D703}_{min}$
, (d)
$\unicode[STIX]{x1D703}_{min}$
, (d)
![]() $V_{0}$
as a function of
$V_{0}$
as a function of
![]() $\tilde{t}$
for various values of
$\tilde{t}$
for various values of
![]() $\unicode[STIX]{x0394}C$
, (e)
$\unicode[STIX]{x0394}C$
, (e)
![]() $\tilde{t}_{SJ}$
as a function of
$\tilde{t}_{SJ}$
as a function of
![]() $\unicode[STIX]{x1D703}_{min}\,({\leqslant}\unicode[STIX]{x1D703}_{max})$
for various values of
$\unicode[STIX]{x1D703}_{min}\,({\leqslant}\unicode[STIX]{x1D703}_{max})$
for various values of
![]() $\unicode[STIX]{x1D703}_{max}$
, and (f)
$\unicode[STIX]{x1D703}_{max}$
, and (f)
![]() $\tilde{t}_{SJ}$
as a function of
$\tilde{t}_{SJ}$
as a function of
![]() $\unicode[STIX]{x1D703}_{max}\,({\geqslant}\unicode[STIX]{x1D703}_{min})$
for various values of
$\unicode[STIX]{x1D703}_{max}\,({\geqslant}\unicode[STIX]{x1D703}_{min})$
for various values of
![]() $\unicode[STIX]{x1D703}_{min}$
. Figure 3 illustrates that
$\unicode[STIX]{x1D703}_{min}$
. Figure 3 illustrates that
![]() $R_{0}$
is constant and
$R_{0}$
is constant and
![]() $\unicode[STIX]{x1D703}_{0}$
is a linearly decreasing function of
$\unicode[STIX]{x1D703}_{0}$
is a linearly decreasing function of
![]() $\tilde{t}$
during each stick phase,
$\tilde{t}$
during each stick phase,
![]() $R_{0}$
and
$R_{0}$
and
![]() $\unicode[STIX]{x1D703}_{0}$
jump instantaneously down and up, respectively, during each jump phase, and as the droplet evaporates the stick phases get progressively shorter (approaching zero duration in the limit
$\unicode[STIX]{x1D703}_{0}$
jump instantaneously down and up, respectively, during each jump phase, and as the droplet evaporates the stick phases get progressively shorter (approaching zero duration in the limit
![]() $n\rightarrow \infty$
).
$n\rightarrow \infty$
).
4 When the saturation concentration depends strongly on temperature
A similar analysis to that described in § 3 can be performed when the saturation concentration of the vapour depends strongly on temperature, corresponding to the asymptotic limit
![]() $\unicode[STIX]{x0394}C\rightarrow \infty$
.
$\unicode[STIX]{x0394}C\rightarrow \infty$
.
Inspection of (2.7)–(2.15) suggests that in the limit
![]() $\unicode[STIX]{x0394}C\rightarrow \infty$
the complete evolution of a droplet will occur over the long time scale
$\unicode[STIX]{x0394}C\rightarrow \infty$
the complete evolution of a droplet will occur over the long time scale
![]() $t=O(\unicode[STIX]{x0394}C)\gg 1$
. Proceeding in the same manner as in § 3 we therefore rescale
$t=O(\unicode[STIX]{x0394}C)\gg 1$
. Proceeding in the same manner as in § 3 we therefore rescale
![]() $c$
and
$c$
and
![]() $J$
with
$J$
with
![]() $1/\unicode[STIX]{x0394}C$
and
$1/\unicode[STIX]{x0394}C$
and
![]() $t$
with
$t$
with
![]() $\unicode[STIX]{x0394}C$
by writing
$\unicode[STIX]{x0394}C$
by writing
![]() $c={\hat{c}}/\unicode[STIX]{x0394}C$
,
$c={\hat{c}}/\unicode[STIX]{x0394}C$
,
![]() $J=\hat{J}/\unicode[STIX]{x0394}C$
and
$J=\hat{J}/\unicode[STIX]{x0394}C$
and
![]() $t=\unicode[STIX]{x0394}C\hat{t}$
, and seek an asymptotic expansion for
$t=\unicode[STIX]{x0394}C\hat{t}$
, and seek an asymptotic expansion for
![]() ${\hat{c}}$
in the form
${\hat{c}}$
in the form
![]() ${\hat{c}}(r,z,\hat{t})={\hat{c}}_{0}(r,z,\hat{t})+O(1/\unicode[STIX]{x0394}C)$
with corresponding asymptotic expansions for the other dependent variables.
${\hat{c}}(r,z,\hat{t})={\hat{c}}_{0}(r,z,\hat{t})+O(1/\unicode[STIX]{x0394}C)$
with corresponding asymptotic expansions for the other dependent variables.
In the limit
![]() $\unicode[STIX]{x0394}C\rightarrow \infty$
we obtain
$\unicode[STIX]{x0394}C\rightarrow \infty$
we obtain
and hence (2.15) yields the equation describing the leading-order evolution of the droplet, namely
In contrast to the limit
![]() $S\rightarrow \infty$
, in this limit we are unable to obtain an explicit expression for the leading-order concentration of vapour,
$S\rightarrow \infty$
, in this limit we are unable to obtain an explicit expression for the leading-order concentration of vapour,
![]() ${\hat{c}}_{0}$
, but, as in the limit
${\hat{c}}_{0}$
, but, as in the limit
![]() $S\rightarrow \infty$
, this is not required in order to determine the leading-order evolution of the droplet.
$S\rightarrow \infty$
, this is not required in order to determine the leading-order evolution of the droplet.
4.1 Evolution of a droplet evaporating in the constant radius mode
A droplet evaporating in the CR mode satisfies
and hence
![]() $\hat{t}_{CR}=F(1,1,S)$
, where
$\hat{t}_{CR}=F(1,1,S)$
, where
![]() $F(R_{0},\unicode[STIX]{x1D703}_{0},S)$
is an increasing function of each of its three arguments defined by
$F(R_{0},\unicode[STIX]{x1D703}_{0},S)$
is an increasing function of each of its three arguments defined by
in which
![]() $\text{Ei}(\cdot )$
denotes the exponential integral
$\text{Ei}(\cdot )$
denotes the exponential integral
Note that
![]() $F(R_{0},\unicode[STIX]{x1D703}_{0},S)$
takes the value zero when any one of its arguments is zero.
$F(R_{0},\unicode[STIX]{x1D703}_{0},S)$
takes the value zero when any one of its arguments is zero.
4.2 Evolution of a droplet evaporating in the constant angle mode
A droplet evaporating in the CA mode satisfies
and hence
![]() $\hat{t}_{CA}=3F(1,1,S)=3\hat{t}_{CR}$
.
$\hat{t}_{CA}=3F(1,1,S)=3\hat{t}_{CR}$
.
Both
![]() $\hat{t}_{CR}$
and
$\hat{t}_{CR}$
and
![]() $\hat{t}_{CA}$
are increasing functions of
$\hat{t}_{CA}$
are increasing functions of
![]() $S$
satisfying
$S$
satisfying
![]() $\hat{t}_{CR},\hat{t}_{CA}=O(1/\log S)\rightarrow 0^{+}$
as
$\hat{t}_{CR},\hat{t}_{CA}=O(1/\log S)\rightarrow 0^{+}$
as
![]() $S\rightarrow 0^{+}$
, and
$S\rightarrow 0^{+}$
, and
![]() $\hat{t}_{CR}\sim S/4\rightarrow \infty$
and
$\hat{t}_{CR}\sim S/4\rightarrow \infty$
and
![]() $\hat{t}_{CA}\sim 3S/4\rightarrow \infty$
as
$\hat{t}_{CA}\sim 3S/4\rightarrow \infty$
as
![]() $S\rightarrow \infty$
, and (as in the limit
$S\rightarrow \infty$
, and (as in the limit
![]() $S\rightarrow \infty$
) their ratio is exactly 3.
$S\rightarrow \infty$
) their ratio is exactly 3.
The solutions in the limit
![]() $\unicode[STIX]{x0394}C\rightarrow \infty$
given by (4.5) and (4.8) are similar, but not identical, to the corresponding solutions in the limit
$\unicode[STIX]{x0394}C\rightarrow \infty$
given by (4.5) and (4.8) are similar, but not identical, to the corresponding solutions in the limit
![]() $S\rightarrow \infty$
given by (3.2) and (3.3) with
$S\rightarrow \infty$
given by (3.2) and (3.3) with
![]() $S$
replaced by
$S$
replaced by
![]() $\unicode[STIX]{x0394}C$
. Unlike the corresponding solutions in the limit
$\unicode[STIX]{x0394}C$
. Unlike the corresponding solutions in the limit
![]() $S\rightarrow \infty$
,
$S\rightarrow \infty$
,
![]() $\unicode[STIX]{x1D703}_{0}$
and
$\unicode[STIX]{x1D703}_{0}$
and
![]() $R_{0}$
are not simply linear functions of
$R_{0}$
are not simply linear functions of
![]() $\hat{t}$
in the CR and CA modes, respectively, and
$\hat{t}$
in the CR and CA modes, respectively, and
![]() $\hat{t}_{CR}$
and
$\hat{t}_{CR}$
and
![]() $\hat{t}_{CA}$
are not simply linear functions of
$\hat{t}_{CA}$
are not simply linear functions of
![]() $S$
. However, except for small values of
$S$
. However, except for small values of
![]() $S$
, the nonlinear function
$S$
, the nonlinear function
![]() $F(R_{0},\unicode[STIX]{x1D703}_{0},S)$
defined by (4.6) is very well approximated by its linear leading-order small
$F(R_{0},\unicode[STIX]{x1D703}_{0},S)$
defined by (4.6) is very well approximated by its linear leading-order small
![]() $R_{0}$
and/or small
$R_{0}$
and/or small
![]() $\unicode[STIX]{x1D703}_{0}$
and/or large
$\unicode[STIX]{x1D703}_{0}$
and/or large
![]() $S$
behaviour, i.e.
$S$
behaviour, i.e.
![]() $F(R_{0},\unicode[STIX]{x1D703}_{0},S)\approx \unicode[STIX]{x1D703}_{0}R_{0}S/4$
. Hence, except for small values of
$F(R_{0},\unicode[STIX]{x1D703}_{0},S)\approx \unicode[STIX]{x1D703}_{0}R_{0}S/4$
. Hence, except for small values of
![]() $S$
, the solutions in the limit
$S$
, the solutions in the limit
![]() $\unicode[STIX]{x0394}C\rightarrow \infty$
are very well approximated by the corresponding solutions in the limit
$\unicode[STIX]{x0394}C\rightarrow \infty$
are very well approximated by the corresponding solutions in the limit
![]() $S\rightarrow \infty$
with
$S\rightarrow \infty$
with
![]() $S$
replaced by
$S$
replaced by
![]() $\unicode[STIX]{x0394}C$
. In particular, except for small values of
$\unicode[STIX]{x0394}C$
. In particular, except for small values of
![]() $S$
,
$S$
,
![]() $\hat{t}_{CR}\approx S/4$
and
$\hat{t}_{CR}\approx S/4$
and
![]() $\hat{t}_{CA}\approx 3S/4$
.
$\hat{t}_{CA}\approx 3S/4$
.
4.3 Evolution of a droplet evaporating in the stick–slide mode
A droplet evaporating in the SS mode satisfies (4.5) for
![]() $0<\tilde{t}<\tilde{t}^{\star }$
and
$0<\tilde{t}<\tilde{t}^{\star }$
and
for
![]() $\hat{t}^{\star }<\hat{t}<\hat{t}_{SS}$
, where
$\hat{t}^{\star }<\hat{t}<\hat{t}_{SS}$
, where
Both
![]() $\hat{t}^{\star }$
and
$\hat{t}^{\star }$
and
![]() $\hat{t}_{SS}$
are increasing functions of
$\hat{t}_{SS}$
are increasing functions of
![]() $S$
satisfying
$S$
satisfying
![]() $\hat{t}^{\star },\hat{t}_{SS}=O(1/\log S)\rightarrow 0^{+}$
as
$\hat{t}^{\star },\hat{t}_{SS}=O(1/\log S)\rightarrow 0^{+}$
as
![]() $S\rightarrow 0^{+}$
, and
$S\rightarrow 0^{+}$
, and
![]() $\hat{t}^{\star }\sim S(1-\unicode[STIX]{x1D703}^{\star })/4\rightarrow \infty$
and
$\hat{t}^{\star }\sim S(1-\unicode[STIX]{x1D703}^{\star })/4\rightarrow \infty$
and
![]() $\hat{t}_{SS}\sim S(1+2\unicode[STIX]{x1D703}^{\star })/4\rightarrow \infty$
as
$\hat{t}_{SS}\sim S(1+2\unicode[STIX]{x1D703}^{\star })/4\rightarrow \infty$
as
![]() $S\rightarrow \infty$
. Furthermore,
$S\rightarrow \infty$
. Furthermore,
![]() $\hat{t}^{\star }$
is a decreasing function of
$\hat{t}^{\star }$
is a decreasing function of
![]() $\unicode[STIX]{x1D703}^{\star }$
satisfying
$\unicode[STIX]{x1D703}^{\star }$
satisfying
![]() $\hat{t}^{\star }=\hat{t}_{CR}$
at
$\hat{t}^{\star }=\hat{t}_{CR}$
at
![]() $\unicode[STIX]{x1D703}^{\star }=0$
and
$\unicode[STIX]{x1D703}^{\star }=0$
and
![]() $\hat{t}^{\star }=0$
at
$\hat{t}^{\star }=0$
at
![]() $\unicode[STIX]{x1D703}^{\star }=1$
, whereas
$\unicode[STIX]{x1D703}^{\star }=1$
, whereas
![]() $\hat{t}_{SS}$
is an increasing function of
$\hat{t}_{SS}$
is an increasing function of
![]() $\unicode[STIX]{x1D703}^{\star }$
satisfying
$\unicode[STIX]{x1D703}^{\star }$
satisfying
![]() $\hat{t}_{SS}=\hat{t}_{CR}$
at
$\hat{t}_{SS}=\hat{t}_{CR}$
at
![]() $\unicode[STIX]{x1D703}^{\star }=0$
and
$\unicode[STIX]{x1D703}^{\star }=0$
and
![]() $\hat{t}_{SS}=\hat{t}_{CA}$
at
$\hat{t}_{SS}=\hat{t}_{CA}$
at
![]() $\unicode[STIX]{x1D703}^{\star }=1$
. As for a droplet evaporating in either the CR or the CA mode, except for small values of
$\unicode[STIX]{x1D703}^{\star }=1$
. As for a droplet evaporating in either the CR or the CA mode, except for small values of
![]() $S$
, the solutions in the limit
$S$
, the solutions in the limit
![]() $\unicode[STIX]{x0394}C\rightarrow \infty$
are again very well approximated by the corresponding solutions in the limit
$\unicode[STIX]{x0394}C\rightarrow \infty$
are again very well approximated by the corresponding solutions in the limit
![]() $S\rightarrow \infty$
with
$S\rightarrow \infty$
with
![]() $S$
replaced by
$S$
replaced by
![]() $\unicode[STIX]{x0394}C$
, and so require no further discussion here.
$\unicode[STIX]{x0394}C$
, and so require no further discussion here.
4.4 Evolution of a droplet evaporating in the stick–jump mode
A droplet evaporating in the SJ mode again satisfies (3.6). During the 1st stick phase with
![]() $R_{0}=R_{1}\equiv 1$
from
$R_{0}=R_{1}\equiv 1$
from
![]() $\hat{t}=\hat{t}_{0}=0$
to
$\hat{t}=\hat{t}_{0}=0$
to
![]() $\hat{t}=\hat{t}_{1}=F(1,1,S)-F(1,\unicode[STIX]{x1D703}_{min},S)$
,
$\hat{t}=\hat{t}_{1}=F(1,1,S)-F(1,\unicode[STIX]{x1D703}_{min},S)$
,
![]() $\unicode[STIX]{x1D703}_{0}$
and
$\unicode[STIX]{x1D703}_{0}$
and
![]() $V_{0}$
are given by (4.5), and thereafter during the
$V_{0}$
are given by (4.5), and thereafter during the
![]() $n$
th stick phase (
$n$
th stick phase (
![]() $n=2,3,4,\ldots$
) with
$n=2,3,4,\ldots$
) with
![]() $R_{0}=R_{n}$
from
$R_{0}=R_{n}$
from
![]() $\hat{t}=\hat{t}_{n-1}$
to
$\hat{t}=\hat{t}_{n-1}$
to
![]() $\hat{t}=\hat{t}_{n}$
,
$\hat{t}=\hat{t}_{n}$
,
where
Taking the limit
![]() $n\rightarrow \infty$
in (4.12) we obtain the lifetime of the droplet, namely
$n\rightarrow \infty$
in (4.12) we obtain the lifetime of the droplet, namely
In particular,
![]() $\hat{t}_{SJ}$
is an increasing function of
$\hat{t}_{SJ}$
is an increasing function of
![]() $S$
satisfying
$S$
satisfying
![]() $\hat{t}_{SJ}\rightarrow 0^{+}$
as
$\hat{t}_{SJ}\rightarrow 0^{+}$
as
![]() $S\rightarrow 0^{+}$
, and
$S\rightarrow 0^{+}$
, and
![]() $\hat{t}_{SJ}=O(S)\rightarrow \infty$
as
$\hat{t}_{SJ}=O(S)\rightarrow \infty$
as
![]() $S\rightarrow \infty$
. Furthermore,
$S\rightarrow \infty$
. Furthermore,
![]() $\hat{t}_{SJ}$
is an increasing function of both
$\hat{t}_{SJ}$
is an increasing function of both
![]() $\unicode[STIX]{x1D703}_{max}$
and
$\unicode[STIX]{x1D703}_{max}$
and
![]() $\unicode[STIX]{x1D703}_{min}\,({<}\unicode[STIX]{x1D703}_{max})$
satisfying
$\unicode[STIX]{x1D703}_{min}\,({<}\unicode[STIX]{x1D703}_{max})$
satisfying
![]() $\hat{t}_{SJ}=\hat{t}_{CR}$
when
$\hat{t}_{SJ}=\hat{t}_{CR}$
when
![]() $\unicode[STIX]{x1D703}_{max}=0$
and when
$\unicode[STIX]{x1D703}_{max}=0$
and when
![]() $\unicode[STIX]{x1D703}_{min}=0$
, and
$\unicode[STIX]{x1D703}_{min}=0$
, and
![]() $\hat{t}_{SJ}\rightarrow \hat{t}_{SS}$
when
$\hat{t}_{SJ}\rightarrow \hat{t}_{SS}$
when
![]() $\unicode[STIX]{x1D703}_{max}\rightarrow \unicode[STIX]{x1D703}_{min}=\unicode[STIX]{x1D703}^{\star }$
. As for a droplet evaporating in either the CR or the CA mode, except for small values of
$\unicode[STIX]{x1D703}_{max}\rightarrow \unicode[STIX]{x1D703}_{min}=\unicode[STIX]{x1D703}^{\star }$
. As for a droplet evaporating in either the CR or the CA mode, except for small values of
![]() $S$
, the solutions in the limit
$S$
, the solutions in the limit
![]() $\unicode[STIX]{x0394}C\rightarrow \infty$
are again very well approximated by the corresponding solutions in the limit
$\unicode[STIX]{x0394}C\rightarrow \infty$
are again very well approximated by the corresponding solutions in the limit
![]() $S\rightarrow \infty$
with
$S\rightarrow \infty$
with
![]() $S$
replaced by
$S$
replaced by
![]() $\unicode[STIX]{x0394}C$
, and so again require no further discussion here.
$\unicode[STIX]{x0394}C$
, and so again require no further discussion here.
5 Conclusions
In the present work we have analysed the evaporation of a thin sessile droplet on a thin substrate in two situations in which the influence of the thermal properties of the system is strong. Specifically, we have obtained uniformly valid leading-order asymptotic solutions for the evolution of the droplet when the substrate has a high thermal resistance relative to the droplet (corresponding to the limit
![]() $S\rightarrow \infty$
with
$S\rightarrow \infty$
with
![]() $\unicode[STIX]{x0394}C\neq 0$
) and when the saturation concentration of the vapour depends strongly on temperature (corresponding to the limit
$\unicode[STIX]{x0394}C\neq 0$
) and when the saturation concentration of the vapour depends strongly on temperature (corresponding to the limit
![]() $\unicode[STIX]{x0394}C\rightarrow \infty$
). In both situations we have obtained explicit expressions for the lifetimes of the droplet for all four of the modes of evaporation studied in the present work (namely the CR, CA, SS and SJ modes).
$\unicode[STIX]{x0394}C\rightarrow \infty$
). In both situations we have obtained explicit expressions for the lifetimes of the droplet for all four of the modes of evaporation studied in the present work (namely the CR, CA, SS and SJ modes).
The basic model, which is applicable when the influence of the thermal properties of the system on the evolution of the droplet is weak, predicts that the lifetimes of the droplet are of the order of the basic time scale (2.2). In contrast, the present work shows that when the influence of the thermal properties of the system on the evolution of the droplet is strong (specifically, in the limit
![]() $S\rightarrow \infty$
and to a very good approximation in the limit
$S\rightarrow \infty$
and to a very good approximation in the limit
![]() $\unicode[STIX]{x0394}C\rightarrow \infty$
), the lifetimes of the droplet are much longer than the basic time scale by a factor of size
$\unicode[STIX]{x0394}C\rightarrow \infty$
), the lifetimes of the droplet are much longer than the basic time scale by a factor of size
![]() $S\unicode[STIX]{x0394}C\gg 1$
, i.e. are actually on the much longer time scale
$S\unicode[STIX]{x0394}C\gg 1$
, i.e. are actually on the much longer time scale
The different dependence of the time scales given by (2.2) and (5.1) on the physical parameters reflects the different dominant physical mechanisms when thermal effects are weak and when they are strong. The basic time scale (2.2), which is independent of
![]() ${\mathcal{L}}$
,
${\mathcal{L}}$
,
![]() $k$
,
$k$
,
![]() $k^{s}$
and
$k^{s}$
and
![]() $h^{s}$
(i.e. independent of the thermal properties of the system and the thickness of the substrate), corresponds to the familiar situation described by the basic diffusion-limited model in which the evaporation from the droplet is limited by diffusion of vapour in the atmosphere with constant saturation concentration at the free surface of the droplet. In contrast, the time scale (5.1), which is independent of
$h^{s}$
(i.e. independent of the thermal properties of the system and the thickness of the substrate), corresponds to the familiar situation described by the basic diffusion-limited model in which the evaporation from the droplet is limited by diffusion of vapour in the atmosphere with constant saturation concentration at the free surface of the droplet. In contrast, the time scale (5.1), which is independent of
![]() $k$
and
$k$
and
![]() $D$
(i.e. independent of the thermal conductivity of the droplet and the coefficient of diffusion of vapour in the atmosphere), corresponds to the situation in which the evaporation from the droplet is limited by thermal conduction through the droplet and the substrate.
$D$
(i.e. independent of the thermal conductivity of the droplet and the coefficient of diffusion of vapour in the atmosphere), corresponds to the situation in which the evaporation from the droplet is limited by thermal conduction through the droplet and the substrate.
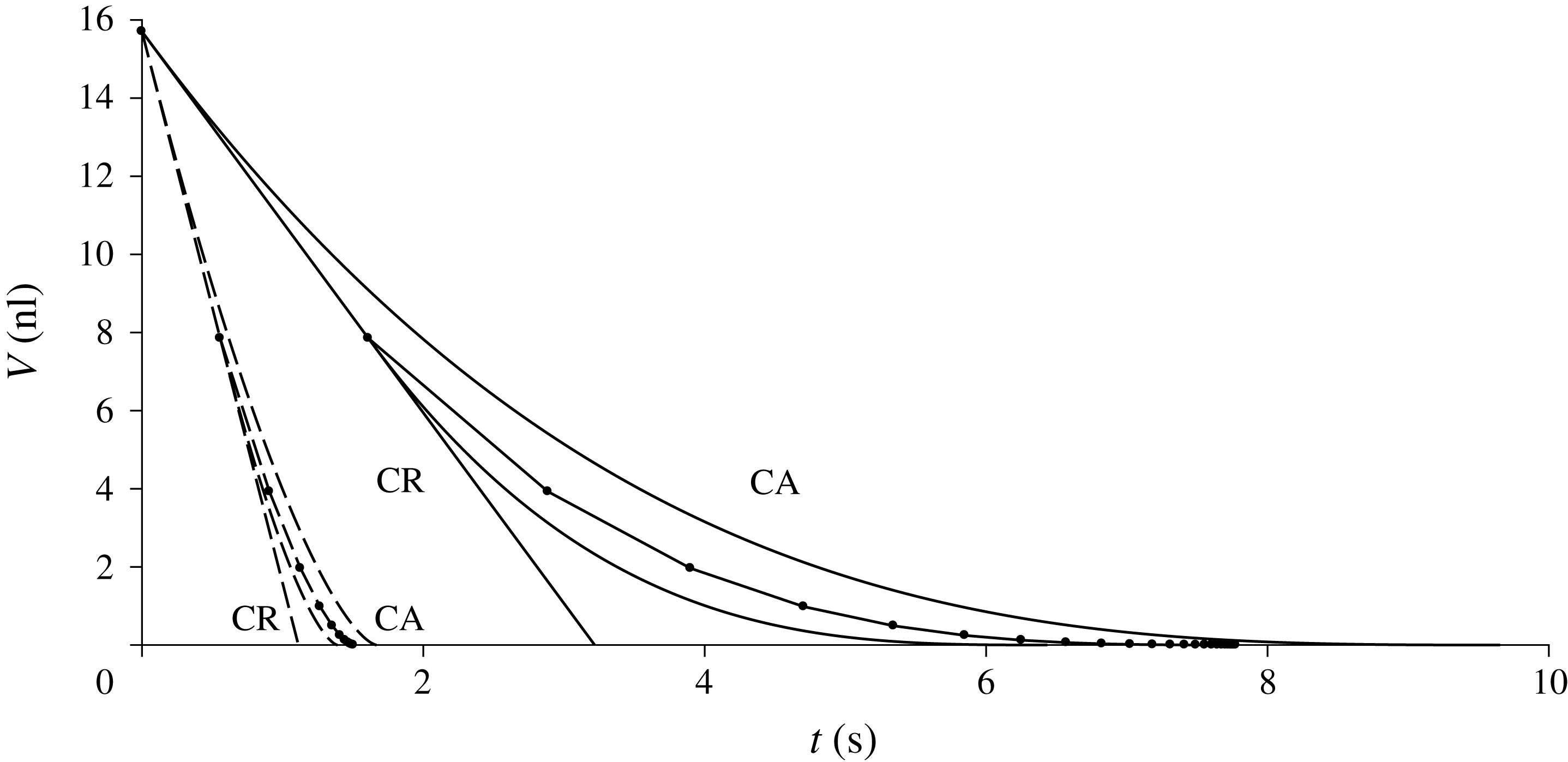
Figure 4. Evolution of the dimensional volume
![]() $V$
(in nl) as a function of dimensional time
$V$
(in nl) as a function of dimensional time
![]() $t$
(in s) for a thin droplet of methanol on a substrate made of a good thermal conductor according to the basic model (dashed curves) and on a thin substrate made of an aerogel according to the present leading-order solution in the limit
$t$
(in s) for a thin droplet of methanol on a substrate made of a good thermal conductor according to the basic model (dashed curves) and on a thin substrate made of an aerogel according to the present leading-order solution in the limit
![]() $S\rightarrow \infty$
with
$S\rightarrow \infty$
with
![]() $\unicode[STIX]{x0394}C\neq 0$
(solid curves). In both cases the four curves correspond (from left to right) to evaporation in the CR, SS, SJ and CA modes. The dots (●) denote the instants at which depinning (SS mode) and the jump phases (SJ mode) occur.
$\unicode[STIX]{x0394}C\neq 0$
(solid curves). In both cases the four curves correspond (from left to right) to evaporation in the CR, SS, SJ and CA modes. The dots (●) denote the instants at which depinning (SS mode) and the jump phases (SJ mode) occur.
To illustrate the difference between the two situations, consider a thin droplet of methanol with initial radius
![]() $R(0)=10^{-3}~\text{m}$
and initial contact angle
$R(0)=10^{-3}~\text{m}$
and initial contact angle
![]() $\unicode[STIX]{x1D703}(0)=0.02$
in an atmosphere of air with
$\unicode[STIX]{x1D703}(0)=0.02$
in an atmosphere of air with
![]() $H=0$
, for which, using the typical parameter values given by Dunn et al. (Reference Dunn, Wilson, Duffy, David and Sefiane2009a
),
$H=0$
, for which, using the typical parameter values given by Dunn et al. (Reference Dunn, Wilson, Duffy, David and Sefiane2009a
),
![]() $\unicode[STIX]{x1D70C}=790~\text{kg}~\text{m}^{-3}$
,
$\unicode[STIX]{x1D70C}=790~\text{kg}~\text{m}^{-3}$
,
![]() ${\mathcal{L}}=1.20\times 10^{6}~\text{m}^{2}~\text{s}^{-2}$
,
${\mathcal{L}}=1.20\times 10^{6}~\text{m}^{2}~\text{s}^{-2}$
,
![]() $k=0.203~\text{kg}~\text{m}~\text{s}^{-3}~\text{K}^{-1}$
,
$k=0.203~\text{kg}~\text{m}~\text{s}^{-3}~\text{K}^{-1}$
,
![]() $c_{sat}(T_{\infty })=0.186~\text{kg}~\text{m}^{-3}$
,
$c_{sat}(T_{\infty })=0.186~\text{kg}~\text{m}^{-3}$
,
![]() $c_{sat}^{\prime }(T_{\infty })=9.47\times 10^{-3}~\text{kg}~\text{m}^{-3}~\text{K}^{-1}$
at
$c_{sat}^{\prime }(T_{\infty })=9.47\times 10^{-3}~\text{kg}~\text{m}^{-3}~\text{K}^{-1}$
at
![]() $T_{\infty }=295$
K and
$T_{\infty }=295$
K and
![]() $D=1.50\times 10^{-5}~\text{m}^{2}~\text{s}^{-1}$
. The basic model predicts that on a substrate made of a good thermal conductor (such as, for example, a metal) the droplet evaporates completely in between 1.11 and 1.67 s (corresponding to the CR and CA modes, respectively). On the other hand, the present leading-order solution in the limit
$D=1.50\times 10^{-5}~\text{m}^{2}~\text{s}^{-1}$
. The basic model predicts that on a substrate made of a good thermal conductor (such as, for example, a metal) the droplet evaporates completely in between 1.11 and 1.67 s (corresponding to the CR and CA modes, respectively). On the other hand, the present leading-order solution in the limit
![]() $S\rightarrow \infty$
with
$S\rightarrow \infty$
with
![]() $\unicode[STIX]{x0394}C\neq 0$
predicts that on a thin substrate of thickness
$\unicode[STIX]{x0394}C\neq 0$
predicts that on a thin substrate of thickness
![]() $h^{s}=2\times 10^{-4}~\text{m}$
made of a poor thermal conductor, specifically an aerogel with a typical thermal conductivity of
$h^{s}=2\times 10^{-4}~\text{m}$
made of a poor thermal conductor, specifically an aerogel with a typical thermal conductivity of
![]() $k^{s}=0.015~\text{kg}~\text{m}~\text{s}^{-3}~\text{K}^{-1}$
(see, for example, Cohen & Glicksman Reference Cohen and Glicksman2015), corresponding to
$k^{s}=0.015~\text{kg}~\text{m}~\text{s}^{-3}~\text{K}^{-1}$
(see, for example, Cohen & Glicksman Reference Cohen and Glicksman2015), corresponding to
![]() $\unicode[STIX]{x0394}C=0.017$
and
$\unicode[STIX]{x0394}C=0.017$
and
![]() $S=135$
, the same droplet evaporates completely in between 3.22 and 9.65 s. Figure 4 shows the evolution of the dimensional volume
$S=135$
, the same droplet evaporates completely in between 3.22 and 9.65 s. Figure 4 shows the evolution of the dimensional volume
![]() $V$
of the droplet as a function of dimensional time
$V$
of the droplet as a function of dimensional time
![]() $t$
for both substrates for all four modes of evaporation. In particular, figure 4 illustrates the main conclusion of the present work, namely that when thermal effects are strong the lifetimes of evaporating droplets are significantly extended relative to those when thermal effects are weak.
$t$
for both substrates for all four modes of evaporation. In particular, figure 4 illustrates the main conclusion of the present work, namely that when thermal effects are strong the lifetimes of evaporating droplets are significantly extended relative to those when thermal effects are weak.
We are unaware of any previous physical experiments against which the present theoretical predictions can be validated, but hope that our work will inspire one or more of the many experimental groups with an interest in evaporating droplets to conduct such experiments in the future.
Although, in order to permit analytical progress, the present analysis was restricted to the case of a thin droplet on a thin substrate, we would anticipate that qualitatively similar behaviour will occur for more general droplets on more general substrates.
Acknowledgements
F.G.H.S. acknowledges the financial support of the United Kingdom Engineering and Physical Sciences Research Council (EPSRC) via EPSRC Doctoral Training Partnership grant EP/N509760/1, the University of Strathclyde, and the University of Edinburgh. K.S. acknowledges financial support from the EVAPORATION Microgravity Application Programme project of the European Space Agency (ESA) (contract number 4200014293). The authors acknowledge valuable discussions with Dr B. R. Duffy and Dr A. W. Wray (University of Strathclyde) on various aspects of droplet evaporation. The authors also wish to thank all three anonymous referees for their insightful comments on the original version of this work.