Published online by Cambridge University Press: 21 August 2013
Evidence of persistent layering, with a vertical stacking of sharp variations in temperature, has been presented recently at the vertical and lateral periphery of energetic oceanic vortices through seismic imaging of the water column. The stacking has vertical scales ranging from a few metres up to 100 m and a lateral spatial coherence of several tens of kilometres comparable with the vortex horizontal size. Inside this layering, in situ data display a 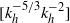 $[{ k}_{h}^{- 5/ 3} { k}_{h}^{- 2} ] $ scaling law of horizontal scales for two different quantities, temperature and a proxy for its vertical derivative, but for two different ranges of wavelengths, between 5 and 50 km for temperature and between 500 m and 5 km for its vertical gradient. In this study, we explore the dynamics underlying the layering formation mechanism, through the slow dynamics captured by quasi-geostrophic equations. Three-dimensional high-resolution numerical simulations of the destabilization of a lens-shaped vortex confirm that the vertical stacking of sharp jumps in density at its periphery is the three-dimensional analogue of the preferential wind-up of potential vorticity near a critical radius, a phenomenon which has been documented for barotropic vortices. For a small-Burger (flat) lens vortex, baroclinic instability ensures a sustained growth rate of sharp jumps in temperature near the critical levels of the leading unstable modes. Such results can be obtained for a background stratification which is due to temperature only and does not require the existence of salt anomalies. Aloft and beneath the vortex core, numerical simulations well reproduce the
$[{ k}_{h}^{- 5/ 3} { k}_{h}^{- 2} ] $ scaling law of horizontal scales for two different quantities, temperature and a proxy for its vertical derivative, but for two different ranges of wavelengths, between 5 and 50 km for temperature and between 500 m and 5 km for its vertical gradient. In this study, we explore the dynamics underlying the layering formation mechanism, through the slow dynamics captured by quasi-geostrophic equations. Three-dimensional high-resolution numerical simulations of the destabilization of a lens-shaped vortex confirm that the vertical stacking of sharp jumps in density at its periphery is the three-dimensional analogue of the preferential wind-up of potential vorticity near a critical radius, a phenomenon which has been documented for barotropic vortices. For a small-Burger (flat) lens vortex, baroclinic instability ensures a sustained growth rate of sharp jumps in temperature near the critical levels of the leading unstable modes. Such results can be obtained for a background stratification which is due to temperature only and does not require the existence of salt anomalies. Aloft and beneath the vortex core, numerical simulations well reproduce the 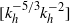 $[{ k}_{h}^{- 5/ 3} { k}_{h}^{- 2} ] $ scaling law of horizontal scales for the vertical derivative of temperature that is observed in situ inside the layering, whatever the background stratification. Such a result stems from the tracer-like behaviour of the vortex stretching component and previous studies have shown that spectra of tracer fields can be steeper than
$[{ k}_{h}^{- 5/ 3} { k}_{h}^{- 2} ] $ scaling law of horizontal scales for the vertical derivative of temperature that is observed in situ inside the layering, whatever the background stratification. Such a result stems from the tracer-like behaviour of the vortex stretching component and previous studies have shown that spectra of tracer fields can be steeper than 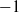 $- 1$, namely in
$- 1$, namely in 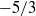 $- 5/ 3$ or
$- 5/ 3$ or 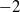 $- 2$, if the advection field is very compact spatially, with a
$- 2$, if the advection field is very compact spatially, with a 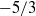 $- 5/ 3$ slope corresponding to a spiral advection of the tracer. Such a scaling law could thus be of geometric origin. As for the kinetic and potential energy, the
$- 5/ 3$ slope corresponding to a spiral advection of the tracer. Such a scaling law could thus be of geometric origin. As for the kinetic and potential energy, the 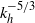 ${ k}_{h}^{- 5/ 3} $ scaling law can be reproduced numerically and is enhanced when the background stratification profile is strongly variable, involving sharp jumps in potential vorticity such as those observed in situ. This raises the possibility of another plausible mechanism leading to a
${ k}_{h}^{- 5/ 3} $ scaling law can be reproduced numerically and is enhanced when the background stratification profile is strongly variable, involving sharp jumps in potential vorticity such as those observed in situ. This raises the possibility of another plausible mechanism leading to a 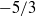 $- 5/ 3$ scaling law, namely surface-quasi-geostrophic (SQG)-like dynamics, although our set-up is more complex than the idealized SQG framework. Energy and enstrophy fluxes have been diagnosed in the numerical quasi-geostrophic simulations. The results emphasize a strong production of energy in the oceanic submesoscales range and a kinetic and potential energy flux from mesoscale to submesoscales range near the critical levels. Such horizontal submesoscale production, which is correlated to the accumulation of thin vertical scales inside the layering, thus has a significant slow dynamical component, well-captured by quasi-geostrophy.
$- 5/ 3$ scaling law, namely surface-quasi-geostrophic (SQG)-like dynamics, although our set-up is more complex than the idealized SQG framework. Energy and enstrophy fluxes have been diagnosed in the numerical quasi-geostrophic simulations. The results emphasize a strong production of energy in the oceanic submesoscales range and a kinetic and potential energy flux from mesoscale to submesoscales range near the critical levels. Such horizontal submesoscale production, which is correlated to the accumulation of thin vertical scales inside the layering, thus has a significant slow dynamical component, well-captured by quasi-geostrophy.
Professor Bach Lien Hua passed away before the final revision of this paper was completed. This manuscript was however written by the first author.