Hostname: page-component-cd9895bd7-mkpzs Total loading time: 0 Render date: 2024-12-28T22:28:40.928Z Has data issue: false hasContentIssue false
  • English
  • Français

Large-scale mean patterns in turbulent convection

Published online by Cambridge University Press:  02 July 2015

Mohammad S. Emran  and
Jörg Schumacher
Mohammad S. Emran*
Affiliation:
Institut für Thermo- und Fluiddynamik, Postfach 100565, Technische Universität Ilmenau, D-98684 Ilmenau, Germany
Jörg Schumacher
Affiliation:
Institut für Thermo- und Fluiddynamik, Postfach 100565, Technische Universität Ilmenau, D-98684 Ilmenau, Germany
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

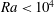Large-scale patterns, which are well-known from the spiral defect chaos (SDC) regime of thermal convection at Rayleigh numbers $\mathit{Ra}<10^{4}$, continue to exist in three-dimensional numerical simulations of turbulent Rayleigh–Bénard convection in extended cylindrical cells with an aspect ratio 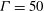${\it\Gamma}=50$ and 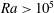$\mathit{Ra}>10^{5}$. They are revealed when the turbulent fields are averaged in time and turbulent fluctuations are thus removed. We apply the Boussinesq closure to estimate turbulent viscosities and diffusivities, respectively. The resulting turbulent Rayleigh number 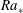$\mathit{Ra}_{\ast }$, that describes the convection of the mean patterns, is indeed in the SDC range. The turbulent Prandtl numbers are smaller than one, with 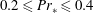$0.2\leqslant \mathit{Pr}_{\ast }\leqslant 0.4$ for Prandtl numbers 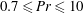$0.7\leqslant \mathit{Pr}\leqslant 10$. Finally, we demonstrate that these mean flow patterns are robust to an additional finite-amplitude sidewall forcing when the level of turbulent fluctuations in the flow is sufficiently high.

JFM classification

Convection: Convection
Type
Papers
Information
Journal of Fluid Mechanics , Volume 776 , 10 August 2015 , pp. 96 - 108
Check for updates
Copyright
© 2015 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Andereck, C. D., Liu, S. S. & Swinney, H. L. 1986 Flow regimes in a circular Couette system with independently rotating cylinders. J. Fluid Mech. 164, 155–183.CrossRefGoogle Scholar
Bailon-Cuba, J., Emran, M. S. & Schumacher, J. 2010 Aspect ratio dependence of heat transfer and large-scale flow in turbulent convection. J. Fluid Mech. 655, 152–173.CrossRefGoogle Scholar
Barkley, D. & Tuckerman, L. S. 2005 Computational study of turbulent laminar patterns in Couette flow. Phys. Rev. Lett. 94, 014502, 1–4.Google Scholar
Bodenschatz, E., de Bryun, J. R., Ahlers, G. & Cannell, D. S. 1991 Transitions between patterns in thermal convection. Phys. Rev. Lett. 67, 3078–3081.Google Scholar
Bodenschatz, E., Pesch, W. & Ahlers, G. 2000 Recent developments in Rayleigh–Bénard convection. Annu. Rev. Fluid Mech. 32, 709–778.CrossRefGoogle Scholar
Busse, F. H. 1978 Nonlinear properties of thermal convection. Rep. Prog. Phys. 41, 1929–1967.Google Scholar
Busse, F. H. 2003 The sequence-of-bifurcations approach towards understanding turbulent fluid flow. Surv. Geophys. 24, 269–288.CrossRefGoogle Scholar
Chiam, K.-H., Paul, M. R., Cross, M. C. & Greenside, H. S. 2003 Mean flow and spiral defect chaos in Rayleigh–Bénard convection. Phys. Rev. E 67, 056206, 1–13.Google Scholar
Chillà, F. & Schumacher, J. 2012 New perspectives in turbulent Rayleigh–Bénard convection. Eur. J. Phys. 35, article no. 58, 1–25.Google ScholarPubMed
Croquette, V. 1989 Convective pattern dynamics at low Prandtl number. Part II. Contemp. Phys. 30, 153–173.Google Scholar
Cross, M. C. & Greenside, H. S. 2009 Pattern Formation and Dynamics in Nonequilibrium Systems. Cambridge University Press.Google Scholar
Cross, M. C. & Hohenberg, P. C. 1993 Pattern formation out of equilibrium. Rev. Mod. Phys. 65, 851–1112.CrossRefGoogle Scholar
Duguet, Y. & Schlatter, P. 2013 Oblique laminar-turbulent interfaces in plane shear flows. Phys. Rev. Lett. 110, 034502, 1–4.Google Scholar
Emran, M. S. & Schumacher, J. 2008 Fine-scale statistics of temperature and its derivatives in convective turbulence. J. Fluid Mech. 611, 13–34.Google Scholar
Emran, M. S. & Schumacher, J. 2010 Lagrangian tracer dynamics in a closed cylindrical turbulent convection cell. Phys. Rev. E 82, 016303, 1–9.CrossRefGoogle Scholar
Grötzbach, G. 1983 Spatial resolution requirements for direct numerical simulation of the Rayleigh–Bénard convection. J. Comput. Phys. 49, 241–269.Google Scholar
Grötzbach, G. 2011 Revisiting the resolution requirements for turbulence simulations in nuclear heat transfer. Nucl. Engng Des. 241, 4379–4390.CrossRefGoogle Scholar
von Hardenberg, J., Parodi, A., Passoni, G., Provenzale, A. & Spiegel, E. A. 2008 Large-scale patterns in Rayleigh–Bénard convection. Phys. Lett. A 372, 2223–2229.CrossRefGoogle Scholar
Hartlep, T., Tilgner, A. & Busse, F. H. 2005 Transition to turbulent convection in a fluid layer heated from below at moderate aspect ratio. J. Fluid Mech. 554, 309–322.Google Scholar
Hoyle, R. 2006 Pattern Formation: An Introduction to Methods. Cambridge University Press.Google Scholar
Kays, W. M. 1994 Turbulent Prandtl number – where are we? Trans. ASME: J. Heat Transfer 116, 284–295.CrossRefGoogle Scholar
Kreilos, T., Zammert, S. & Eckhardt, B. 2014 Comoving frames and symmetry-related motions in parallel shear flows. J. Fluid Mech. 751, 685–697.CrossRefGoogle Scholar
Kurtuldu, H., Mischaikow, K. & Schatz, M. F. 2011 Extensive scaling from computational homology and Karhunen–Loève decomposition analysis of Rayleigh–Bénard convection experiments. Phys. Rev. Lett. 107, 034503, 1–4.Google Scholar
Malecha, Z., Chini, G. & Julien, K. 2014 A multiscale algorithm for simulating spatially–extended Langmuir circulation dynamics. J. Comput. Phys. 271, 131–150.Google Scholar
Morris, S. W., Bodenschatz, E., Cannell, D. S. & Ahlers, G. 1991 Spiral defect chaos in large aspect ratio Rayleigh–Bénard convection. Phys. Rev. Lett. 71, 2026–2029.Google Scholar
Nakano, T., Fukushima, T., Unno, W. & Kondo, M. 1979 Viscosity, conductivity, and power spectra of the turbulent convection in Boussinesq fluids. Publ. Astron. Soc. Japan 31, 713–735.Google Scholar
Shams, A., Roelofs, F., Baglietto, E., Lardeau, S. & Kenjeres, S. 2014 Assessment and calibration of an algebraic turbulent heat flux model for low-Prandtl fluids. Intl J. Heat Mass Transfer 79, 589–601.Google Scholar
Shishkina, O., Stevens, R. A. J. M., Grossmann, S. & Lohse, D. 2010 Boundary layer structure in turbulent thermal convection and its consequences for the required numerical resolution. New J. Phys. 12, 075022, 1–17.CrossRefGoogle Scholar
Silano, G., Sreenivasan, K. R. & Verzicco, R. 2010 Numerical simulations of Rayleigh–Bénard convection for Prandtl numbers between $10^{-1}$ and $10^{4}$ and Rayleigh numbers between $10^{5}$ and $10^{9}$ . J. Fluid Mech. 662, 409–446.Google Scholar
Spiegel, E. A. 1971 Convection in stars: I. Basic Boussinesq convection. Annu. Rev. Astron. Astrophys. 9, 323–352.Google Scholar
Verzicco, R. & Camussi, R. 2003 Numerical experiments on strongly turbulent thermal convection in a slender cylindrical cell. J. Fluid Mech. 477, 19–49.CrossRefGoogle Scholar
Wilcox, D. C. 2006 Turbulence Modeling for CFD. DCW Industries.Google Scholar