Hostname: page-component-586b7cd67f-t8hqh Total loading time: 0 Render date: 2024-11-26T14:23:19.206Z Has data issue: false hasContentIssue false
  • English
  • Français

Large-scale contribution to mean wall shear stress in high-Reynolds-number flat-plate boundary layers up to 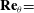$\mathbf{Re}_{\boldsymbol{\theta}}{=}$13650

Published online by Cambridge University Press:  04 March 2014

Sébastien Deck ,
Nicolas Renard ,
Romain Laraufie  and
Pierre-Élie Weiss
Sébastien Deck*
Affiliation:
ONERA, The French Aerospace Lab, F-92190 Meudon, France
Nicolas Renard
Affiliation:
ONERA, The French Aerospace Lab, F-92190 Meudon, France
Romain Laraufie
Affiliation:
ONERA, The French Aerospace Lab, F-92190 Meudon, France
Pierre-Élie Weiss
Affiliation:
ONERA, The French Aerospace Lab, F-92190 Meudon, France
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

A numerical investigation of the mean wall shear stress properties on a spatially developing turbulent boundary layer over a smooth flat plate was carried out by means of a zonal detached eddy simulation (ZDES) technique for the Reynolds number range 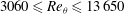$3060\leq Re_{\theta }\leq 13\, 650$. Some asymptotic trends of global parameters are suggested. Consistently with previous findings, the calculation confirms the occurrence of very large-scale motions approximately 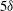$5\delta $ to 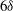$6 \delta $ long which are meandering with a lateral amplitude of 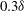$0.3 \delta $ and which maintain a footprint in the near-wall region. It is shown that these large scales carry a significant amount of Reynolds shear stress and their influence on the skin friction, denoted 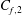$C_{f,2}$, is revisited through the FIK identity by Fukagata, Iwamoto & Kasagi (Phys. Fluids, vol. 14, 2002, p. L73). It is argued that 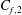$C_{f,2}$ is the relevant parameter to characterize the high-Reynolds-number turbulent skin friction since the term describing the spatial heterogeneity of the boundary layer also characterizes the total shear stress variations across the boundary layer. The behaviour of the latter term seems to follow some remarkable self-similarity trends towards high Reynolds numbers. A spectral analysis of the weighted Reynolds stress with respect to the distance to the wall and to the wavelength is provided for the first time to our knowledge and allows us to analyse the influence of the largest scales on the skin friction. It is shown that structures with a streamwise wavelength 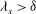$\lambda _x >\delta $ contribute to more than 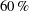$60\, \%$ of $C_{f,2}$, and that those larger than 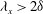$\lambda _x >2\delta $ still represent approximately 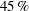$45\, \%$ of 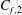$C_{f,2}$.

JFM classification

Boundary Layers: Boundary layer structure Turbulent Flows: Turbulence simulation
Type
Papers
Information
Journal of Fluid Mechanics , Volume 743 , 25 March 2014 , pp. 202 - 248
Copyright
© 2014 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Adrian, R. J., Meinhart, C. D. & Tomkins, C. D. 2000 Vortex organization in the outer region of the turbulent boundary layer. J. Fluid Mech. 422, 1–54.Google Scholar
del Álamo, J. C. & Jiménez, J. 2009 Estimation of turbulent convection velocities and corrections to Taylor’s approximation. J. Fluid Mech. 640, 5–26.Google Scholar
del Álamo, J. C., Jiménez, J., Zandonade, P. & Moser, R. D. 2004 Scaling of the energy spectra of turbulent channels. J. Fluid Mech. 500, 135–144.CrossRefGoogle Scholar
Araya, G., Castillo, L., Meneveau, C. & Jansen, K. 2011 A dynamic multi-scale approach for turbulent inflow boundary conditions in spatially developing flows. J. Fluid Mech. 670, 581–605.Google Scholar
Balakumar, B. J. & Adrian, R. J. 2007 Large- and very-large-scale motions in channel and boundary-layer flows. Phil. Trans. R. Soc. Lond. A 365, 665–681.Google Scholar
Bernardini, M. & Pirozzoli, S. 2011 Inner/outer layer interactions in turbulent boundary layers: A refined measure for the large-scale amplitude modulation mechanism. Phys. Fluids 23, 061701.Google Scholar
Carlier, J. & Stanislas, M. 2005 Experimental study of eddy structures in a turbulent boundary layer using particle image velocimetry. J. Fluid Mech. 535, 143–188.Google Scholar
Choi, H. & Moin, P. 1994 Compact finite difference schemes with spectral-like resolution. J. Comput. Phys. 113 (1), 227–234.Google Scholar
Coles, D. E. 1956 The law of the wake in the turbulent boundary layer. J. Fluid Mech. 1, 191–226.Google Scholar
Dandois, J., Garnier, E. & Sagaut, P. 2007 Numerical simulation of active separation control by a synthetic jet. J. Fluid Mech. 574, 25–58.Google Scholar
Deck, S. 2005a Numerical simulation of transonic buffet over a supercritical airfoil. AIAA J. 43 (7), 1556–1566.Google Scholar
Deck, S. 2005b Zonal-detached eddy simulation of the flow around a high-lift configuration. AIAA J. 43 (11), 2372–2384.Google Scholar
Deck, S. 2012 Recent improvements of the Zonal Detached Eddy Simulation (ZDES) formulation. Theor. Comput. Fluid Dyn. 26 (6), 523–550.CrossRefGoogle Scholar
Deck, S., Duveau, Ph., d’Espiney, P. & Guillen, Ph. 2002 Development and application of Spalart Allmaras one equation turbulence model to three-dimensional supersonic complex configurations. Aerosp. Sci. Technol. 6 (3), 171–183.Google Scholar
Deck, S. & Laraufie, R. 2013 Numerical investigation of the flow dynamics past a three-element aerofoil. J. Fluid Mech. 723, 401–444.CrossRefGoogle Scholar
Deck, S. & Thorigny, P. 2007 Unsteadiness of an axisymmetric separating-reattaching flow: Numerical investigation. Phys. Fluids 19, 065103.Google Scholar
Deck, S., Weiss, P. E., Pamiès, M. & Garnier, E. 2011 Zonal detached eddy simulation of a spatially developing flat plate turbulent boundary layer. Comput. Fluids 48, 1–15.Google Scholar
DeGraaff, D. B. & Eaton, J. K. 2000 Reynolds number scaling of the flat-plate turbulent boundary layer. J. Fluid Mech. 422, 319–346.Google Scholar
Dennis, D. J. C. & Nickels, T. B. 2008 On the limitations of Taylor’s hypothesis in constructing long structures in a turbulent boundary layer. J. Fluid Mech. 614, 197–206.Google Scholar
Erm, L. P. & Joubert, P. N. 1991 Low-Reynolds-number turbulent boundary layers. J. Fluid Mech. 230, 1–44.Google Scholar
Fernholz, H. H. & Finley, P. J. 1996 The incompressible zero-pressure-gradient turbulent boundary layer: an assessment of the data. Prog. Aerosp. Sci. 32, 245–311.Google Scholar
Ferrante, A. & Elghobashi, S. E. 2009 Reynolds number effect on drag reduction in a microbubble-laden spatially developing boundary layer. J. Fluid Mech. 543, 93–106.Google Scholar
Fukagata, K., Iwamoto, K. & Kasagi, N. 2002 Contribution of Reynolds stress distribution to the skin friction in wall-bounded flows. Phys. Fluids 14, 73–76.Google Scholar
Ganapathisubramani, B., Clemens, N. T. & Dolling, D. S. 2006 Large-scale motions in a supersonic turbulent boundary layer. J. Fluid Mech. 556, 271–282.CrossRefGoogle Scholar
Ganapathisubramani, B., Hutchins, N., Monty, J. P., Chung, D. & Marusic, I. 2012 Amplitude and frequency modulation in wall turbulence. J. Fluid Mech. 712, 61–91.Google Scholar
Ganapathisubramani, B., Longmire, E. K. & Marusic, I. 2003 Characteristics of vortex packets in turbulent boundary layers. J. Fluid Mech. 478, 35–46.Google Scholar
Gand, F., Deck, S., Brunet, V. & Sagaut, P. 2010 Dynamics over a simplified junction flow. Phys. Fluids 22, 115111.Google Scholar
Gomez, T., Flutet, V. & Sagaut, P. 1981 Contribution of Reynolds stress distribution to the skin friction in compressible turbulent channel flows. Phys. Rev. E 79, 035301–1/4.Google Scholar
Head, M. R. & Bandyopadhyay, P. 1981 New aspects of turbulent boundary layer structure. J. Fluid Mech. 107, 297–338.Google Scholar
Hoyas, S. & Jimenez, J. 2006 Scaling of velocity fluctuations in turbulent channels up to $Re_{\tau }=2003$ . Phys. Fluids 18, 011702.Google Scholar
Hudgins, L., Friehe, C. A. & Mayer, M. E. 1993 Wavelet transforms and atmospheric turbulence. Phys. Rev. Lett. 71 (20), 3279–3282.CrossRefGoogle Scholar
Hultmark, M., Vallikivi, M., Bailey, S. C. C. & Smits, A. J. 2013 Logarithmic scaling of turbulence in smooth- and rough-wall pipe flow. J. Fluid Mech. 728, 376–395.Google Scholar
Hutchins, N., Chauhan, K., Marusic, I., Monty, J. & Klewicki, J. 2012 Towards reconciling the large-scale structure of turbulent boundary layers in the atmosphere and laboratory. Boundary-Layer Meteorol. 145, 273–306.CrossRefGoogle Scholar
Hutchins, N. & Marusic, I. 2007 Evidence of very long meandering features in the logarithmic region of turbulent boundary layers. J. Fluid Mech. 579, 1–28.CrossRefGoogle Scholar
Hutchins, N., Monty, J. P., Ganapathisubramani, B., Ng, H. C. H. & Marusic, I. 2011 Three-dimensional conditional structure of a high-Reynolds-number turbulent boundary layer. J. Fluid Mech. 673, 255–285.Google Scholar
Hutchins, N., Nickels, T. B., Marusic, I. & Chong, M. S. 2009 Hot-wire spatial resolution issues in wall-bounded turbulence. J. Fluid Mech. 635, 103–136.CrossRefGoogle Scholar
Hwang, Y. 2013 Near-wall turbulent fluctuations in the absence of wide outer motions. J. Fluid Mech. 723, 264–288.Google Scholar
Ishihara, T., Gotoh, T. & Kaneda, Y. 2009 Study of high-Reynolds number isotropic turbulence by direct numerical simulation. Annu. Rev. Fluid Mech. 41, 165–180.CrossRefGoogle Scholar
Jarrin, N., Benhamadouche, S., Laurence, D. & Prosser, R. 2006 A synthetic-eddy-method for generating inflow conditions for large eddy simulation. Intl J. Heat Fluid Flow 27, 585–593.Google Scholar
Jiménez, J.1998 The largest scales of turbulent wall flows. CTR Annu. Res. Briefs pp. 137–154. Center for Turbulence Research.Google Scholar
Jiménez, J. 2003 Computing high-Reynolds-number turbulence: will simulations ever replace experiments?. J. Turbul. 4 (22), 14.CrossRefGoogle Scholar
Jiménez, J. 2012 Cascades in wall-bounded turbulence. Annu. Rev. Fluid Mech. 44, 27–45.CrossRefGoogle Scholar
Jiménez, J., del Álamo, J. C. & Flores, O. 2004 The large-scale dynamics of near-wall turbulence. J. Fluid Mech. 505, 179–199.Google Scholar
Jiménez, J., Hoyas, S., Simens, M. P. & Mizuno, Y. 2010 Turbulent boundary layers and channels at moderate Reynolds numbers. J. Fluid Mech. 657, 335–360.Google Scholar
Jiménez, J. & Pinelli, A. 1999 The autonomous cycle of near-wall turbulence. J. Fluid Mech. 389, 335–359.Google Scholar
Kaneda, Y. & Ishihara, T. 2006 High-resolution direct numerical simulation of turbulence. J. Turbul. 7 (20), 14.CrossRefGoogle Scholar
Kaneda, Y., Morishita, K. & Ishihara, T. 2013 Small scale universality and spectral characteristics in turbulent flows. In Symposium on Turbulence and Shear Flow Phenomena (TSFP-8), Poitiers, France .Google Scholar
Klewicki, J. C. 2010 Reynolds number dependence, scaling, and dynamics of turbulent boundary layers. Trans. ASME: J. Fluids Engng 132, 094001.Google Scholar
Krogstad, P.-Å., Antonia, R. A. & Browne, L. W. B. 1992 Comparison between rough- and smooth-wall turbulent boundary layers. J. Fluid Mech. 245, 599–617.Google Scholar
Krogstad, P.-Å., Kaspersen, J. H. & Rimestad, S. 1998 Convection velocities in a turbulent boundary layer. Phys. Fluids 10 (4), 949–957.CrossRefGoogle Scholar
Kunkel, G. J. & Marusic, I. 2006 Study of the near-wall-turbulent region of the high-Reynolds-number boundary layer using an atmospheric flow. J. Fluid Mech. 548, 375–402.CrossRefGoogle Scholar
Laraufie, R. & Deck, S. 2013 Assessment of Reynolds stresses tensor reconstruction methods for synthetic inflow conditions. Application to hybrid RANS/LES methods. Intl J. Heat Fluid Flow 42, 68–78.Google Scholar
Laraufie, R., Deck, S. & Sagaut, P. 2011 A dynamic forcing method for unsteady turbulent inflow conditions. J. Comput. Phys. 230 (23), 8647–8663.CrossRefGoogle Scholar
Laraufie, R., Deck, S. & Sagaut, P. 2012 A rapid switch from RANS to WMLES for spatially developing boundary layers. In Progress in Hybrid RANS-LES Modelling (ed. Fu, S., Haase, W., Peng, S.-H. & Schwamborn, D.), vol. 117, pp. 147–156. Springer.CrossRefGoogle Scholar
Larchevêque, L., Sagaut, P., Le, T. H. & Comte, P. 1997 Large-eddy simulation of a compressible flow in a three-dimensional open cavity at high Reynolds number. J. Fluid Mech. 516, 265–301.Google Scholar
Lee, J., Jung, S. Y., Sung, H. J. & Zaki, T. A. 2013 Effect of wall heating on turbulent boundary layers with temperature-dependent viscosity. J. Fluid Mech. 726, 196–225.Google Scholar
Lee, J. H. & Sung, H. J. 2011 Direct numerical simulation of a turbulent boundary layer up to $Re_{\theta }=2500$ . Intl J. Heat Fluid Flow 32, 1–10.Google Scholar
Lee, J. H. & Sung, H. J. 2013 Comparison of very-large-scale motions of turbulent pipe and boundary layer simulations. Phys. Fluids 25, 045103.Google Scholar
Marquillie, M., Ehrenstein, U. & Laval, J.-P. 2011 Instability of streaks in wall turbulence with adverse pressure gradient. J. Fluid Mech. 681, 205–240.Google Scholar
Marusic, I. & Heuer, W. D. C. 2007 Reynolds number invariance of the structure inclination angle in wall turbulence. Phys. Rev. Lett. 99, 114504.Google Scholar
Marusic, I. & Hutchins, N. 2005 Experimental study of wall turbulence: implications for control. In Transition And Turbulence Control. (ed. Gad-el-Hak, M. & Tsai, H. M.), Lecture Notes Series, Institute for Mathematical Sciences, National University of Singapore, vol. 8, pp. 1–40.Google Scholar
Marusic, I. & Kunkel, G. J. 2003 Streamwise turbulence intensity formulation for flat-plate boundary layers. Phys. Fluids 15, 2461–2464.Google Scholar
Marusic, I., Li, J. D. & Perry, A. E. 1989 A study of the Reynolds-shear-stress spectra in zero-pressure-gradient boundary layers. In Tenth Australian Fluid Mechanics Conference – University of Melbourne .Google Scholar
Marusic, I., Mathis, R. & Hutchins, N. 2010a High Reynolds number effects in wall turbulence. Intl J. Heat Fluid Flow 31, 418–428.Google Scholar
Marusic, I., Mathis, R. & Hutchins, N. 2010b Predictive model for wall-bounded turbulent flow. Science 329, 193–196.Google Scholar
Marusic, I., McKeon, B. J., Monkewitz, P. A., Nagib, H. M., Smits, A. J. & Sreenivasan, K. R. 2010 Wall-bounded turbulent flows at high Reynolds numbers: Recent advances and key issues. Phys. Fluids 22, 065103.Google Scholar
Marusic, I., Monty, J. P., Hultmark, M. & Smits, A. J. 2012 On the logarithmic region in wall turbulence. J. Fluid Mech. 716, 1–11.Google Scholar
Marusic, I., Uddin, A. K. M. & Perry, A. E. 1997 Similarity law for the streamwise turbulence intensity in zero-pressure-gradient turbulent boundary layers. Phys. Fluids 9, 3718–3726.Google Scholar
Mary, I. & Sagaut, P. 2002 Large eddy simulation of flow around an airfoil near stall. AIAA J. 40 (6), 1139–1145.Google Scholar
Mathis, R., Hutchins, N. & Marusic, I. 2009 Large-scale amplitude modulation of the small-scale structures in turbulent boundary layers. J. Fluid Mech. 628, 311–337.Google Scholar
Mathis, R., Marusic, I., Chernyshenko, S. I. & Hutchins, N. 2013 Estimating wall-shear-stress fluctuations given an outer region input. J. Fluid Mech. 715, 163–180.Google Scholar
Mathis, R., Marusic, I., Hutchins, N. & Sreenivasan, K. R. 2011 The relationship between the velocity skewness and the amplitude modulation of the small scale by the large scale in turbulent boundary layers. Phys. Fluids 23, 121702.Google Scholar
Michel, R., Quémard, C. & Durant, R. 1969 Application d’un schéma de longueur de mélange à l’étude des couches limites turbulentes d’équilibre. ONERA Note Tech. 154.Google Scholar
Nagib, H. M., Chauhan, K. A. & Monkewitz, P. A. 2007 Approach to an asymptotic state for zero pressure gradient turbulent boundary layer. Phil. Trans. R. Soc. Lond. A 365, 755–770.Google Scholar
Nagib, H. M., Christophorou, C., Reudi, J.-D., Monkewitz, P. A., Österlund, J. & Gravante, S. 2004 Can we ever rely on results from wall-bounded turbulent flows without direct measurements of wall shear stress?. In 24th AIAA Aerodynamic Measurement Technology and Ground Testing Conference .Google Scholar
Nickels, T. B. & Marusic, I. 2001 On the different contributions of coherent structures to the spectra of a turbulent round jet and a turbulent boundary layer. J. Fluid Mech. 448, 367–385.Google Scholar
Österlund, J. M., Johansson, A. V., Nagib, H. M. & Hites, M. 2000 A note on the overlap region in turbulent boundary layers. Phys. Fluids 12, 1–4.Google Scholar
Pamiès, M., Weiss, P. E., Deck, S. & Sagaut, P. 2009 Generation of synthetic turbulent inflow data for large eddy simulation of spatially evolving wall-bounded flows. Phys. Fluids 21, 045103.Google Scholar
Panton, R. L. 2001 Overview of the self-sustaining mechanisms of wall turbulence. Prog. Aerosp. Sci. 37, 341–383.Google Scholar
Péchier, T. V., Guillen, L. G. & Caysac, M. A. 2001 Magnus effect over finned projectiles. AIAA J. Spacecr. Rockets 38 (4), 542–549.Google Scholar
Peet, Y. & Sagaut, P. 2009 Theoretical prediction of skin friction on geometrically complex surface. Phys. Fluids 21, 105105.Google Scholar
Perry, A. E. & Marusic, I. 1995 A wake model for the turbulence structure of boundary layers. Part 1. Extension of the attached eddy hypothesis. J. Fluid Mech. 298, 361–388.Google Scholar
Perry, A. E., Marusic, I. & Jones, M. B. 2002 On the streamwise evolution of turbulent boundary layers in arbitrary pressure gradients. J. Fluid Mech. 461, 61–91.Google Scholar
Pirozzoli, S. & Bernardini, M. 2013 Probing high-Reynolds number effects in numerical boundary layers. Phys. Fluids 25, 021704.Google Scholar
Priyadarshana, P. J. A. & Klewicki, J. C. 2004 Study of the motions contributing to the Reynolds stress in high and low Reynolds number turbulent boundary layers. Phys. Fluids 16, 4586–4600.Google Scholar
Robinson, S. K. 1991 Coherent motions in the turbulent boundary layer. Annu. Rev. Fluid Mech. 23, 601–639.Google Scholar
Saddoughi, S. G. & Veeravalli, S. V. 1994 Local isotropy in turbulent boundary layers at high Reynolds number. J. Fluid Mech. 268, 333–372.CrossRefGoogle Scholar
Sagaut, P. & Deck, S. 2009 Large eddy simulation for aerodynamics: Status and perspectives. Phil. Trans. R. Soc. Lond. A 367, 2849–2860.Google Scholar
Sagaut, P., Deck, S. & Terracol, M. 2013 Multiscale and Multiresolution Approaches in Turbulence: A Comprehensive Introduction to Modern LES, DES and Hybrid RANS/LES Methods with Examples. 2nd Edn. Imperial College Press.Google Scholar
Schlatter, P., Li, Q., Brethouwer, G., Johansson, A. & Henningson, D. 2010 Simulations of spatially evolving turbulent boundary layers up to $Re_{\theta }=4300$ . Intl J. Heat Fluid Flow 31, 251–261.Google Scholar
Schlatter, P. & Örlü, R. 2010a Assessment of direct simulation data of turbulent boundary layers. J. Fluid Mech. 659, 116–126.Google Scholar
Schlatter, P. & Örlü, R. 2010b Quantifying the interaction between large and small scales in wall-bounded turbulent flows: A note of caution. Phys. Fluids 22, 051704.Google Scholar
Schlichting, H. 1968 Boundary-Layer Theory. McGraw-Hill.Google Scholar
Sillero, J., Jimenez, J., Moser, R. D. & Malaya, N. P. 2011 Direct simulation of a zero-pressure-gradient turbulent boundary layer up to $Re_{\theta }=6650$ . In 13th European Turbulence Conference (ETC13), J. Phys.: Conf. Series 318, 022023. IOP.Google Scholar
Simens, M. P., Jiménez, J., Hoyas, S. & Mizuno, Y. 2009 A high-resolution code for turbulent boundary layers. J. Comput. Phys. 228, 4218–4231.Google Scholar
Simon, F., Deck, S., Guillen, Ph., Sagaut, P. & Merlen, A. 2007 Numerical simulation of the compressible mixing layer past an axisymmetric trailing edge. J. Fluid Mech. 591, 215–253.Google Scholar
Smith, R. W. 1994 Effect of Reynolds number on the structure of turbulent boundary layers. PhD thesis, Department of Mechanical and Aerospace Engineering, Princeton University.Google Scholar
Smits, A. J., McKeon, B. J. & Marusic, I. 2011 High Reynolds number wall turbulence. Annu. Rev. Fluid Mech. 43 (1), 353–375.Google Scholar
Spalart, P. R. 1988 Direct simulation of a turbulent boundary layer up to $Re_{\theta }=1400$ . J. Fluid Mech. 187, 61–98.CrossRefGoogle Scholar
Spalart, P. R. & Allmaras, S. R. 1992 A one equation turbulence model for aerodynamic flows. AIAA Paper 92-0439.Google Scholar
Townsend, A. A. 1976 The Structure of Turbulent Shear Flow. Cambridge University Press.Google Scholar
Tromeur, E., Garnier, E. & Sagaut, P. 2006 ES of aero-optical effects in turbulent boundary layer. J. Turbul. 7 (1), 28.Google Scholar
Weiss, P. E. & Deck, S. 2011 Control of the antisymmetric mode ( $m=1$ ) for high Reynolds axisymmetric separating/reattaching flows. Phys. Fluids 23, 095102.Google Scholar
Weiss, P. E., Deck, S., Robinet, J. C. & Sagaut, P. 2009 On the dynamics of axisymmetric turbulent separating/reattaching flows. Phys. Fluids 21, 075103.Google Scholar
Wu, X. & Moin, P. 2009 Direct numerical simulation of turbulence in a nominally zero-pressure gradient flat-plate boundary layer. J. Fluid Mech. 630, 5–41.CrossRefGoogle Scholar