Hostname: page-component-848d4c4894-8bljj Total loading time: 0 Render date: 2024-07-04T22:36:05.213Z Has data issue: false hasContentIssue false
  • English
  • Français

Large-eddy simulation study of unsteady wake dynamics and geometric sensitivity on a skewed bump

Published online by Cambridge University Press:  27 December 2019

David S. Ching Open the ORCID record for David S. Ching [Opens in a new window]  and
John K. Eaton
David S. Ching*
Affiliation:
Department of Mechanical Engineering, Stanford University, 488 Escondido Mall, Stanford, CA94305, USA
John K. Eaton
Affiliation:
Department of Mechanical Engineering, Stanford University, 488 Escondido Mall, Stanford, CA94305, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

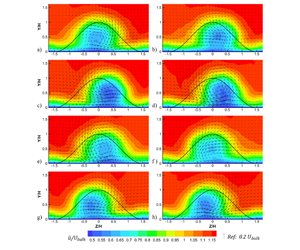
Large-eddy simulations of a skewed bump are performed with the bump at angles of $10^{\circ }$ and $50^{\circ }$ with respect to the free stream. The wake has a large separation bubble and unsteady vortex structures that are highly sensitive to the bump angle. The $10^{\circ }$ bump has secondary separation with forward-facing flow in the main separation bubble. The Reynolds stress suggests large-scale motions in the wake, but are insufficient to understand the shedding dynamics. The quasi-periodic shedding cycle is reconstructed using spectral proper orthogonal decomposition. For the $10^{\circ }$ case, opposite-sign streamwise vortices are alternately advected downstream in the wake, but only a single vortex is distinguishable in the $50^{\circ }$ case. The wake streamwise velocity pulses twice each cycle in the $10^{\circ }$ bump, but once per cycle in the $50^{\circ }$ bump. The separation bubble and wake oscillate in the spanwise direction. Conditional averaging shows that the vortices are associated with low streamwise velocity and high turbulence. Surface pressures on the bump have negatively skewed distributions in regions on the upstream face and in the separation bubble. In the separation bubble, fluctuations associated with the shedding cycle contribute to the negative skewness.

JFM classification

Vortex Flows: Vortex shedding Wakes/Jets: Separated flows Wakes/Jets: Wakes
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 885 , 25 February 2020 , A22
Copyright
© 2019 Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

AbuOmar, M. M. & Martinuzzi, R. J. 2008 Vortical structures around a surface-mounted pyramid in a thin boundary layer. J. Wind Engng Ind. Aerodyn. 96 (6–7), 769–778.CrossRefGoogle Scholar
Bourgeois, J. A., Sattari, P. & Martinuzzi, R. J. 2011 Alternating half-loop shedding in the turbulent wake of a finite surface-mounted square cylinder with a thin boundary layer. Phys. Fluids 23 (9), 095101.CrossRefGoogle Scholar
Byun, G. & Simpson, R. L. 2006 Structure of three-dimensional separated flow on an axisymmetric bump. AIAA J. 44 (5), 999–1008.CrossRefGoogle Scholar
Byun, G. & Simpson, R. L. 2010 Surface-pressure fluctuations from separated flow over an axisymmetric bump. AIAA J. 48 (10), 2397–2405.CrossRefGoogle Scholar
Byun, G., Simpson, R. L. & Long, C. H. 2004 Study of vortical separation from three-dimensional symmetric bumps. AIAA J. 42 (4), 754–765.CrossRefGoogle Scholar
Cabot, W. & Moin, P. 2000 Approximate wall boundary conditions in the large-eddy simulation of high Reynolds number flow. Flow Turbul. Combust. 63 (1–4), 269–291.CrossRefGoogle Scholar
Cherry, E. M., Elkins, C. J. & Eaton, J. K. 2008 Geometric sensitivity of three-dimensional separated flows. Intl J. Heat Fluid Flow 29 (3), 803–811.CrossRefGoogle Scholar
Ching, D. S., Elkins, C. J. & Eaton, J. K. 2018a Investigation of geometric sensitivity of a non-axisymmetric bump: 3D mean velocity measurements. Exp. Fluids 59, 143.CrossRefGoogle Scholar
Ching, D. S., Elkins, C. J. & Eaton, J. K. 2018b Unsteady vortex structures in the wake of non-axisymmetric bumps using spiral MRV. Exp. Fluids 59, 144.CrossRefGoogle Scholar
Clemens, N. T. & Narayanaswamy, V. 2014 Low-frequency unsteadiness of shock wave/turbulent boundary layer interactions. Annu. Rev. Fluid Mech. 46, 469–492.CrossRefGoogle Scholar
Eaton, J. K. & Johnston, J. P. 1982 Low frequency unsteadyness of a reattaching turbulent shear layer. In Turbulent Shear Flows 3, pp. 162–170. Springer.CrossRefGoogle Scholar
Eibeck, P. A. & Eaton, J. K. 1987 Heat transfer effects of a longitudinal vortex embedded in a turbulent boundary layer. J. Heat Transfer 109 (1), 16–24.CrossRefGoogle Scholar
Ericsson, L. E. & Reding, J. P. 1981 Steady and unsteady vortex-induced asymmetric loads on slender vehicles. J. Spacecraft 18 (2), 97–109.CrossRefGoogle Scholar
García-Villalba, M., Wissink, J. G. & Rodi, W. 2010 Influence of the approach boundary layer on the flow over an axisymmetric hill at a moderate Reynolds number. J. Turbul. 11 (8), 1–20.Google Scholar
Ghaemi, S. & Scarano, F. 2013 Turbulent structure of high-amplitude pressure peaks within the turbulent boundary layer. J. Fluid Mech. 735, 381–426.CrossRefGoogle Scholar
Gravante, S. P., Naguib, A. M., Wark, C. E. & Nagib, H. M. 1998 Characterization of the pressure fluctuations under a fully developed turbulent boundary layer. AIAA J. 36 (10), 1808–1816.CrossRefGoogle Scholar
Graziani, A., Kerhervé, F., Martinuzzi, R. J. & Keirsbulck, L. 2018 Dynamics of the recirculating areas of a forward-facing step. Exp. Fluids 59 (10), 154.CrossRefGoogle Scholar
Hajimirzaie, S. M., Wojcik, C. J. & Buchholz, J. H. J. 2012 The role of shape and relative submergence on the structure of wakes of low-aspect-ratio wall-mounted bodies. Exp. Fluids 53 (6), 1943–1962.CrossRefGoogle Scholar
Ham, F. 2007 An efficient scheme for large eddy simulation of low-Ma combustion in complex configurations. In Annual Research Briefs, Center for Turbulence Research, Stanford University, Stanford, CA, pp. 41–46.Google Scholar
Hunt, B. 1982 Asymmetric vortex forces and wakes on slender bodies. In AIAA 9th Atmospheric Flight Mechanics Conference, p. 1336. AIAA.Google Scholar
Hunt, J. C. R., Wray, A. A. & Moin, P. 1988 Eddies, streams, and convergence zones in turbulent flows. In Proceedings of the Summer Program 1988, pp. 193–208.Google Scholar
Karangelen, C. C., Wilczynski, V. & Casarella, M. J. 1993 Large amplitude wall pressure events beneath a turbulent boundary layer. J. Fluids Engng 115 (4), 653–659.CrossRefGoogle Scholar
Kim, J. 1989 On the structure of pressure fluctuations in simulated turbulent channel flow. J. Fluid Mech. 205, 421–451.CrossRefGoogle Scholar
Kiya, M. & Sasaki, K. 1983 Structure of a turbulent separation bubble. J. Fluid Mech. 137, 83–113.CrossRefGoogle Scholar
Klewicki, J. C., Priyadarshana, P. J. A. & Metzger, M. M. 2008 Statistical structure of the fluctuating wall pressure and its in-plane gradients at high Reynolds number. J. Fluid Mech. 609, 195–220.CrossRefGoogle Scholar
Kravchenko, A. G. & Moin, P. 2000 Numerical studies of flow over a circular cylinder at Re D = 3900. Phys. Fluids 12 (2), 403–417.CrossRefGoogle Scholar
Le, H., Moin, P. & Kim, J. 1997 Direct numerical simulation of turbulent flow over a backward-facing step. J. Fluid Mech. 330, 349–374.CrossRefGoogle Scholar
Lumley, J. L. 1970 Stochastic Tools in Turbulence. Courier Corporation.Google Scholar
Marshall, J. S. 2001 Inviscid Incompressible Flow. John Wiley & Sons.Google Scholar
Martinuzzi, R. J. & AbuOmar, M. 2003 Study of the flow around surface-mounted pyramids. Exp. Fluids 34 (3), 379–389.CrossRefGoogle Scholar
Mason, P. J. & Morton, B. R. 1987 Trailing vortices in the wakes of surface-mounted obstacles. J. Fluid Mech. 175, 247–293.CrossRefGoogle Scholar
Matsumura, M. & Antonia, R. A. 1993 Momentum and heat transport in the turbulent intermediate wake of a circular cylinder. J. Fluid Mech. 250, 651–668.CrossRefGoogle Scholar
McCarthy, J. M., Giacobello, M. & Lam, S. 2019 Wavelet coherence of surface pressure fluctuations due to von Kármán vortex shedding near a hemispherical protuberance. Exp. Fluids 60 (1), 3.CrossRefGoogle Scholar
Moffatt, H. K. 1964 Viscous and resistive eddies near a sharp corner. J. Fluid Mech. 18 (1), 1–18.CrossRefGoogle Scholar
Na, Y. & Moin, P. 1998a Direct numerical simulation of a separated turbulent boundary layer. J. Fluid Mech. 374, 379–405.CrossRefGoogle Scholar
Na, Y. & Moin, P. 1998b The structure of wall-pressure fluctuations in turbulent boundary layers with adverse pressure gradient and separation. J. Fluid Mech. 377, 347–373.CrossRefGoogle Scholar
Parnaudeau, P., Carlier, J., Heitz, D. & Lamballais, E. 2008 Experimental and numerical studies of the flow over a circular cylinder at Reynolds number 3900. Phys. Fluids 20 (8), 085101.CrossRefGoogle Scholar
Pattenden, R. J., Turnock, S. R. & Zhang, X. 2005 Measurements of the flow over a low-aspect-ratio cylinder mounted on a ground plane. Exp. Fluids 39 (1), 10–21.CrossRefGoogle Scholar
Sattari, P., Bourgeois, J. A. & Martinuzzi, R. J. 2012 On the vortex dynamics in the wake of a finite surface-mounted square cylinder. Exp. Fluids 52 (5), 1149–1167.CrossRefGoogle Scholar
Sayles, E. L. & Eaton, J. K. 2014 Sensitivity of an asymmetric, three-dimensional diffuser to inlet condition perturbations. Intl J. Heat Fluid Flow 49, 100–107.CrossRefGoogle Scholar
Schewe, G. 1983 On the structure and resolution of wall-pressure fluctuations associated with turbulent boundary-layer flow. J. Fluid Mech. 134, 311–328.CrossRefGoogle Scholar
Simpson, R. L., Long, C. H. & Byun, G. 2002 Study of vortical separation from an axisymmetric hill. Intl J. Heat Fluid Flow 23 (5), 582–591.CrossRefGoogle Scholar
Steinwolf, A. & Rizzi, S. A. 2006 Non-Gaussian analysis of turbulent boundary layer fluctuating pressure on aircraft skin panels. J. Aircraft 43 (6), 1662–1675.CrossRefGoogle Scholar
Suzuki, Y., Kiya, M., Sampo, T. & Naka, Y. 1987 Pressure fluctuations on the surface of a hemisphere immersed in a thick turbulent boundary layer. J. Fluids Engng 109 (2), 130–135.CrossRefGoogle Scholar
Touber, E. & Sandham, N. D. 2009 Large-eddy simulation of low-frequency unsteadiness in a turbulent shock-induced separation bubble. Theor. Comput. Fluid Dyn. 23 (2), 79–107.CrossRefGoogle Scholar
Towne, A., Schmidt, O. T. & Colonius, T. 2018 Spectral proper orthogonal decomposition and its relationship to dynamic mode decomposition and resolvent analysis. J. Fluid Mech. 847, 821–867.CrossRefGoogle Scholar
Tsuji, Y., Fransson, J. H. M., Alfredsson, P. H. & Johansson, A. V. 2007 Pressure statistics and their scaling in high-Reynolds-number turbulent boundary layers. J. Fluid Mech. 585, 1–40.CrossRefGoogle Scholar
Van Oudheusden, B. W., Scarano, F., Van Hinsberg, N. P. & Watt, D. W. 2005 Phase-resolved characterization of vortex shedding in the near wake of a square-section cylinder at incidence. Exp. Fluids 39 (1), 86–98.CrossRefGoogle Scholar
Vreman, A. W. 2004 An eddy-viscosity subgrid-scale model for turbulent shear flow: algebraic theory and applications. Phys. Fluids 16 (10), 3670–3681.CrossRefGoogle Scholar
Weiss, J., Mohammed-Taifour, A. & Schwaab, Q. 2015 Unsteady behavior of a pressure-induced turbulent separation bubble. In 53rd AIAA Aerospace Sciences Meeting, p. 1289. AIAA.Google Scholar
Williamson, C. H. K. 1996 Vortex dynamics in the cylinder wake. Annu. Rev. Fluid Mech. 28 (1), 477–539.CrossRefGoogle Scholar
Xie, Z.-T. & Castro, I. P. 2008 Efficient generation of inflow conditions for large eddy simulation of street-scale flows. Flow Turbul. Combust. 81 (3), 449–470.CrossRefGoogle Scholar