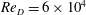 $Re_{D}=6\times 10^{4}$
$Re_{D}=6\times 10^{4}$Published online by Cambridge University Press: 19 September 2018
We present wall-resolved large-eddy simulation (LES) of flow with free-stream velocity 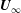 $\boldsymbol{U}_{\infty }$ over a cylinder of diameter
$\boldsymbol{U}_{\infty }$ over a cylinder of diameter 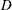 $D$ rotating at constant angular velocity
$D$ rotating at constant angular velocity 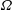 $\unicode[STIX]{x1D6FA}$, with the focus on the lift crisis, which takes place at relatively high Reynolds number
$\unicode[STIX]{x1D6FA}$, with the focus on the lift crisis, which takes place at relatively high Reynolds number 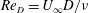 $Re_{D}=U_{\infty }D/\unicode[STIX]{x1D708}$, where
$Re_{D}=U_{\infty }D/\unicode[STIX]{x1D708}$, where  $\unicode[STIX]{x1D708}$ is the kinematic viscosity of the fluid. Two sets of LES are performed within the (
$\unicode[STIX]{x1D708}$ is the kinematic viscosity of the fluid. Two sets of LES are performed within the ( $Re_{D}$,
$Re_{D}$,  $\unicode[STIX]{x1D6FC}$)-plane with
$\unicode[STIX]{x1D6FC}$)-plane with 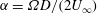 $\unicode[STIX]{x1D6FC}=\unicode[STIX]{x1D6FA}D/(2U_{\infty })$ the dimensionless cylinder rotation speed. One set, at
$\unicode[STIX]{x1D6FC}=\unicode[STIX]{x1D6FA}D/(2U_{\infty })$ the dimensionless cylinder rotation speed. One set, at 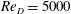 $Re_{D}=5000$, is used as a reference flow and does not exhibit a lift crisis. Our main LES varies
$Re_{D}=5000$, is used as a reference flow and does not exhibit a lift crisis. Our main LES varies  $\unicode[STIX]{x1D6FC}$ in
$\unicode[STIX]{x1D6FC}$ in 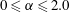 $0\leqslant \unicode[STIX]{x1D6FC}\leqslant 2.0$ at fixed
$0\leqslant \unicode[STIX]{x1D6FC}\leqslant 2.0$ at fixed  $Re_{D}=6\times 10^{4}$. For
$Re_{D}=6\times 10^{4}$. For  $\unicode[STIX]{x1D6FC}$ in the range
$\unicode[STIX]{x1D6FC}$ in the range 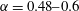 $\unicode[STIX]{x1D6FC}=0.48{-}0.6$ we find a lift crisis. This range is in agreement with experiment although the LES shows a deeper local minimum in the lift coefficient than the measured value. Diagnostics that include instantaneous surface portraits of the surface skin-friction vector field
$\unicode[STIX]{x1D6FC}=0.48{-}0.6$ we find a lift crisis. This range is in agreement with experiment although the LES shows a deeper local minimum in the lift coefficient than the measured value. Diagnostics that include instantaneous surface portraits of the surface skin-friction vector field 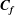 $\boldsymbol{C}_{\boldsymbol{f}}$, spanwise-averaged flow-streamline plots, and a statistical analysis of local, near-surface flow reversal show that, on the leeward-bottom cylinder surface, the flow experiences large-scale reorganization as
$\boldsymbol{C}_{\boldsymbol{f}}$, spanwise-averaged flow-streamline plots, and a statistical analysis of local, near-surface flow reversal show that, on the leeward-bottom cylinder surface, the flow experiences large-scale reorganization as  $\unicode[STIX]{x1D6FC}$ increases through the lift crisis. At
$\unicode[STIX]{x1D6FC}$ increases through the lift crisis. At 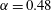 $\unicode[STIX]{x1D6FC}=0.48$ the primary-flow features comprise a shear layer separating from that side of the cylinder that moves with the free stream and a pattern of oscillatory but largely attached flow zones surrounded by scattered patches of local flow separation/reattachment on the lee and underside of the cylinder surface. Large-scale, unsteady vortex shedding is observed. At
$\unicode[STIX]{x1D6FC}=0.48$ the primary-flow features comprise a shear layer separating from that side of the cylinder that moves with the free stream and a pattern of oscillatory but largely attached flow zones surrounded by scattered patches of local flow separation/reattachment on the lee and underside of the cylinder surface. Large-scale, unsteady vortex shedding is observed. At 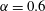 $\unicode[STIX]{x1D6FC}=0.6$ the flow has transitioned to a more ordered state where the small-scale separation/reattachment cells concentrate into a relatively narrow zone with largely attached flow elsewhere. This induces a low-pressure region which produces a sudden decrease in lift and hence the lift crisis. Through this process, the boundary layer does not show classical turbulence behaviour. As
$\unicode[STIX]{x1D6FC}=0.6$ the flow has transitioned to a more ordered state where the small-scale separation/reattachment cells concentrate into a relatively narrow zone with largely attached flow elsewhere. This induces a low-pressure region which produces a sudden decrease in lift and hence the lift crisis. Through this process, the boundary layer does not show classical turbulence behaviour. As  $\unicode[STIX]{x1D6FC}$ is further increased at constant
$\unicode[STIX]{x1D6FC}$ is further increased at constant 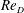 $Re_{D}$, the localized separation zone dissipates with corresponding attached flow on most of the cylinder surface. The lift coefficient then resumes its increasing trend. A logarithmic region is found within the boundary layer at
$Re_{D}$, the localized separation zone dissipates with corresponding attached flow on most of the cylinder surface. The lift coefficient then resumes its increasing trend. A logarithmic region is found within the boundary layer at 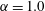 $\unicode[STIX]{x1D6FC}=1.0$.
$\unicode[STIX]{x1D6FC}=1.0$.