Hostname: page-component-745bb68f8f-f46jp Total loading time: 0 Render date: 2025-01-09T18:02:35.432Z Has data issue: false hasContentIssue false
  • English
  • Français

Large eddy simulation of flow over a twisted cylinder at a subcritical Reynolds number

Published online by Cambridge University Press:  27 October 2014

Jae Hwan Jung  and
Hyun Sik Yoon
Jae Hwan Jung
Affiliation:
Department of Naval Architecture and Ocean Engineering, Pusan National University, San 30, Jangjeon-Dong, Gumjeong-Gu, Busan 609-735, Korea
Hyun Sik Yoon*
Affiliation:
Global Core Research Center for Ships and Offshore Plants, Pusan National University, San 30, Jangjeon-Dong, Gumjeong-Gu, Busan 609-735, Korea
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We consider a twisted cylinder that was designed by rotating the elliptic cross-section along the spanwise direction, resulting in a passive control. The flow over the twisted cylinder is investigated at a subcritical Reynolds number (Re) of 3000 using large eddy simulation based on the finite volume method. For comparison, the flow past smooth and wavy cylinders is also calculated. The twisted cylinder achieves reductions of approximately 13 and 5 % in mean drag compared with smooth and wavy cylinders, respectively. In particular, the root mean square (r.m.s.) value of the lift fluctuation of the twisted cylinder shows a substantial decrease of approximately 96 % compared with the smooth cylinder. The shear layer of the twisted cylinder covering the recirculation region is more elongated than those of the smooth and wavy cylinders, and vortex shedding from the twisted cylinder is considerably suppressed. Consequently, the elongation of the shear layer from the body and the near disappearance of vortex shedding in the near wake with weak vortical strength contributes directly to the reduction of drag and lift oscillation. Various fundamental mechanisms that affect the flow phenomena, three-dimensional separation, pressure coefficient, vortex formation length and turbulent kinetic energy are examined systematically to demonstrate the effect of the twisted cylinder surface. 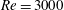In addition, for the twisted cylinder at $\mathit{Re}=3000$, the effect of the cross-sectional aspect ratio is investigated from 1.25 to 2.25 to find an optimal value that can reduce the drag and lift forces. Moreover, the effect of the Reynolds number on the aerodynamic characteristics is investigated in the range of 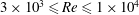$3\times 10^{3}\leqslant \mathit{Re}\leqslant 1\times 10^{4}$. We find that as Re increases, the mean drag and the r.m.s. lift coefficient of the twisted cylinder increase, and the vortex formation length decreases.

JFM classification

Flow Control: Flow Control Vortex Flows: Vortex shedding Wakes/Jets: Wakes
Type
Papers
Information
Journal of Fluid Mechanics , Volume 759 , 25 November 2014 , pp. 579 - 611
Check for updates
Copyright
© 2014 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Ahmed, A. & Bays-Muchmore, B. 1992 Transverse flow over a wavy cylinder. Phys. Fluids A 4, 1959–1967.Google Scholar
Ahmed, A., Khan, M. J. & Bays-Muchmore, B. 1993 Experimental investigation of a three-dimensional bluff-body wake. AIAA J. 31, 559–563.Google Scholar
Bearman, P. W. 1965 Investigation of the flow behind a two-dimensional model with a blunt trailing edge and fitted with splitter plates. J. Fluid Mech. 21, 241–255.Google Scholar
Bishop, R. E. D. & Hassan, A. Y. 1964 The lift and drag forces on a circular cylinder in a flowing fluid. Proc. R. Soc. Lond. A 277, 32–50.Google Scholar
Bloor, M. S. 1964 The transition to turbulence in the wake of a circular cylinder. J. Fluid Mech. 19, 290–304.Google Scholar
Breuer, M. 1998 Large eddy simulation of the subcritical flow past a circular cylinder: numerical and modeling aspects. Intl J. Numer. Meth. Fluids 28, 1281–1302.Google Scholar
Breuer, M. 2000 A challenging test case for large eddy simulation: high Reynolds number circular cylinder. Intl J. Heat Fluid Flow 21, 648–654.Google Scholar
Choi, H., Jeon, W.-P. & Kim, J. 2008 Control of flow over a bluff body. Annu. Rev. Fluid Mech. 40, 113–139.Google Scholar
Chyu, C. K. & Rockwell, D. 2002 Near-wake flow structure of a cylinder with a helical surface perturbation. J. Fluids Struct. 16, 263–269.CrossRefGoogle Scholar
Deardoff, J. W. 1970 A numerical study of three-dimensional turbulent channel flow at large Reynolds numbers. J. Fluid Mech. 41, 453–480.Google Scholar
Dong, S., Karniadakis, G. E., Ekmekci, A. & Rockwell, D. 2006 A combined direct numerical simulation–particle image velocimetry study of the turbulent near wake. J. Fluid Mech. 569, 185–207.Google Scholar
Drazin, P. G. & Reid, W. H. 1981 Hydrodynamic Stability. Cambridge University Press.Google Scholar
Germano, M., Piomelli, U., Moin, P. & Cabot, W. H. 1991 A dynamic subgrid-scale eddy viscosity model. Phys. Fluids A 3, 1760–1765.CrossRefGoogle Scholar
Gerrard, J. H. 1978 The wakes of cylindrical bluff bodies at low Reynolds number. Phil. Trans. R. Soc. Lond. A 288, 351–382.Google Scholar
Gopalkrishnan, R.1993 Vortex-induced forces on oscillating bluff cylinders. PhD thesis, Department of Ocean Engineering, MIT, Cambridge, MA, USA.Google Scholar
Govardhan, R. & Williamson, C. H. K. 2001 Mean and fluctuating velocity fields in the wake of a freely-vibrating cylinder. J. Fluids Struct. 15, 489–501.CrossRefGoogle Scholar
Jordan, S. A. 2002 Investigation of the cylinder separated shear-layer physics by large-eddy simulation. Intl J. Heat Fluid Flow 23, 1–12.Google Scholar
Jordan, S. A. & Ragab, S. A. 1998 A large-eddy simulation of the near wake of a circular cylinder. Trans. ASME: J. Fluids Engng 120, 243–252.Google Scholar
Keefe, R. T. 1962 Investigation of the fluctuating forces acting on a stationary circular cylinder in a subsonic stream and of the associated sound field. J. Acoust. Soc. Am. 34, 1711–1714.Google Scholar
Kim, J. & Choi, H. 2005 Distributed forcing of flow over a circular cylinder. Phys. Fluids 17, 033103.Google Scholar
Kim, J. & Moin, P. 1985 Application of a fractional step method to incompressible Navier–Stokes equations. J. Comput. Phys. 59, 308–323.Google Scholar
Lam, K. & Lin, Y. F. 2007 Drag force control of flow over wavy cylinders at low Reynolds number. J. Mech. Sci. Technol. 21, 1331–1337.CrossRefGoogle Scholar
Lam, K. & Lin, Y. F. 2008 Large eddy simulation of flow around wavy cylinders at a subcritical Reynolds number. Intl J. Heat Fluid Flow 29, 1071–1088.Google Scholar
Lam, K. & Lin, Y. F. 2009 Effects of wavelength and amplitude of a wavy cylinder in cross-flow at low Reynolds numbers. J. Fluid Mech. 620, 195–220.Google Scholar
Lam, K., Wang, F. H., Li, J. Y. & So, R. M. C. 2004a Experimental investigation of the mean and fluctuating forces of wavy (varicose) cylinders in a cross-flow. J. Fluids Struct. 19, 321–334.Google Scholar
Lam, K., Wang, F. H. & So, R. M. C. 2004b Three-dimensional nature of vortices in the near wake of a wavy cylinder. J. Fluids Struct. 19, 815–833.CrossRefGoogle Scholar
Lee, S. J. & Kim, H. B. 1997 The effect of surface protrusions on the near wake of a circular cylinder. J. Wind Engng Ind. Aerodyn. 69–71, 351–361.Google Scholar
Lee, S. J. & Nguyen, A. T. 2007 Experimental investigation on wake behind a wavy cylinder having sinusoidal cross-sectional area variation. Fluid Dyn. Res. 39, 292–304.Google Scholar
Lilly, D. K. 1992 A proposed modification of the Germano subgrid-scale closure method. Phys. Fluids 4, 633–635.Google Scholar
Lin, J.-C., Towfighi, J. & Rockwell, D. 1995 Instantaneous structure of the near-wake of a circular cylinder: on the effect of Reynolds number. J. Fluids Struct. 9, 409–418.Google Scholar
Lu, X., Dalton, C. & Zhang, J. 1997 Application of large eddy simulation to flow past a circular cylinder. J. Offshore Mech. Arctic Engng 119, 219–225.Google Scholar
Lugt, H. J. & Haussling, H. J. 1974 Laminar flow past an abruptly accelerated elliptic cylinder at 45 $^{\circ }$ incidence. J. Fluid Mech. 65, 711–734.Google Scholar
Modi, V. J. & Dikshii, A. K. 1975 Near-wakes of elliptic cylinders in subcritical flow. AIAA J. 13, 490–497.Google Scholar
Moeller, M. J.1982 Measurement of unsteady forces on a circular cylinder in cross flow at subcritical Reynolds numbers. PhD thesis, Department of Ocean Engineering, MIT, Cambridge, MA, USA.Google Scholar
Moeller, M. J. & Leehey, P. 1984 Unsteady forces on a cylinder in cross flow at subcritical Reynolds numbers. In ASME Symposium on Flow-induced Vibrations, New Orleans (ed. Paidoussis, M. P., Griffin, O. M. & Sevik, M.), vol. 1, pp. 57–71. ASME.Google Scholar
Nair, M. T. & Sengupta, T. K. 1997 Unsteady flow past elliptic cylinders. J. Fluids Struct. 11, 555–595.Google Scholar
Nebres, J., Barill, S. & Nelson, R. 1993 Flow about yawed, stranded cables. Exp. Fluids 14, 49–58.Google Scholar
Norberg, C.1987 Effects of Reynolds number and a low-intensity freestream turbulence on the flow around a circular cylinder. Publ. 87/2. Department of Applied Thermodynamics and Fluid Mechanics. Chalmers University of Technology.Google Scholar
Norberg, C. 1993 Pressure forces on a circular cylinder in cross flow. In Bluff Body Wakes, Dynamics and Instabilities, Proc. IUTAM Symposium. 115, 7–11 September 1992 (ed. Eckelmann, H., Graham, J. M., Huerre, P. & Monkewitz, P. A.), Springer.Google Scholar
Norberg, C. 1994 An experimental investigation of the flow around a circular cylinder: influence of aspect ratio. J. Fluid Mech. 258, 287–316.Google Scholar
Norberg, C.1998 LDV-measurements in the near wake of a circular cylinder. In Proc. the ASME Fluids Eng. Div. Summer Meeting, Washington, DC, Paper 4. Also ASME, FEDSM98-5202.Google Scholar
Norberg, C. 2003 Fluctuating lift on a circular cylinder: review and new measurements. J. Fluids Struct. 17, 57–96.Google Scholar
Ota, T., Nishiyama, H. & Taoka, Y. 1984 Heat transfer and flow around an elliptic cylinder. Intl J. Heat Mass Transfer 27, 1771–1779.Google Scholar
Owen, J. C., Bearman, P. W. & Szewczyk, A. A. 2001 Passive control of VIV with drag reduction. J. Fluids Struct. 15, 597–605.Google Scholar
Park, N., Lee, S., Lee, J. & Choi, H. 2006 A dynamic subgrid-scale eddy-viscosity model with a global coefficient. Phys. Fluids 18, 125109.Google Scholar
Piomelli, U. 1999 Large-eddy simulation: achievements and challenges. Prog. Aerosp. Sci. 35, 335–362.Google Scholar
Singh, S. & You, D. 2013 A dynamic global-coefficient mixed subgrid-scale model for large-eddy simulation of turbulent flows. Intl J. Heat Fluid Flow 42, 94–104.Google Scholar
Smagorinsky, J. 1963 General circulation experiments with the primitive equations. I. The basic experiment. Mon. Weath. Rev. 91, 99–164.Google Scholar
Tadrist, H., Martin, R., Tadrist, L. & Seguin, P. 1990 Experimental investigation of fluctuating forces exerted on a circular cylinder tube (Reynolds numbers from 3000 to 30 000). Phys. Fluids A 2, 2176–2182.Google Scholar
Tanida, Y., Okajima, A. & Watanabe, Y. 1973 Stability of a circular cylinder oscillating in uniform flow or in a wake. J. Fluid Mech. 61, 769–784.Google Scholar
Unal, M. F. & Rockwell, D. 1988 On vortex formation from a cylinder. Part 1. The initial instability. J. Fluid Mech. 190, 491–512.Google Scholar
Weaver, W. 1961 Wind-induced vibrations in antenna members. ASCE J. Engng Mech. Div. 87 (EM1), 141–168.Google Scholar
West, G. S. & Apelt, C. J. 1993 Measurements of fluctuating pressures and forces on a circular cylinder in the Reynolds number range $10^{4}$ to $2.5\times 10^{5}$ . J. Fluids Struct. 7, 227–244.Google Scholar
White, F. W. 1974 Viscous Fluid Flow. McGraw-Hill.Google Scholar
Williamson, C. H. K. 1996 Vortex dynamics in the cylinder wake. Annu. Rev. Fluid Mech. 28, 477–539.Google Scholar
Williamson, C. H. K. & Govardhan, R. 2004 Vortex-induced vibrations. Annu. Rev. Fluid Mech. 36, 413–455.Google Scholar
Wu, J.-Z., Lu, X.-Y. & Zhuang, L.-X. 2007 Integral force acting on a body due to local flow structures. J. Fluid Mech. 576, 265–286.CrossRefGoogle Scholar
Wu, J., Sheridan, J. & Welsh, M. C. 1996 Velocity perturbations induced by the longitudinal vortices in a cylinder wake. Trans. ASME: J. Fluids Engng 118, 531–536.Google Scholar
Xu, C. Y., Chen, L.-W. & Lu, X. Y. 2010 Large-eddy simulation of the compressible flow past a wavy cylinder. J. Fluid Mech. 665, 238–273.Google Scholar
Yeo, D. H. & Jones, N. P. 2011 Computational study on aerodynamic mitigation of wind-induced, large-amplitude vibrations of stay cables with strakes. J. Wind Engng Ind. Aerodyn. 99, 389–399.Google Scholar
Yoon, H. S., Balachandar, S. & Ha, M. Y. 2009 Large eddy simulation of flow in an unbaffled stirred tank for different Reynolds numbers. Phys. Fluids 21, 1–16.Google Scholar
You, D. & Moin, P. 2007 A dynamic global-coefficient subgrid-scale eddy-viscosity model for large-eddy simulation in complex geometries. Phys. Fluids 19, 065110.Google Scholar
You, D. & Moin, P. 2009 A dynamic global-coefficient subgrid-scale model for large eddy simulation of turbulent scalar transport in complex geometries. Phys. Fluids 21, 045109.Google Scholar
Zang, Y., Street, R. L. & Koseff, J. R. 1994 A non-staggered grid, fractional step method for time-dependent incompressible Navier–Stokes equations in curvilinear coordinates. J. Comput. Phys. 114, 18–33.Google Scholar
Zdravkovich, M. M. 1981 Review and classification of various aerodynamic and hydrodynamic means for suppressing vortex shedding. J. Wind Engng Ind. Aerodyn. 7, 145–189.Google Scholar
Zhang, W., Dai, C. & Lee, S. J. 2005 PIV measurements of the near-wake behind a sinusoidal cylinder. Exp. Fluids 38, 824–832.Google Scholar
Zhou, J., Adrian, R. J., Balachandar, S. & Kendall, T. M. 1999 Mechanisms for generating coherent packets of hairpin vorticies in channel flow. J. Fluid Mech. 387, 353–396.Google Scholar