Hostname: page-component-cd9895bd7-gxg78 Total loading time: 0 Render date: 2024-12-28T21:08:20.009Z Has data issue: false hasContentIssue false
  • English
  • Français

Large coherence of spanwise velocity in turbulent boundary layers

Published online by Cambridge University Press:  21 May 2018

Charitha M. de Silva Open the ORCID record for Charitha M. de Silva [Opens in a new window] ,
Kevin Kevin Open the ORCID record for Kevin Kevin [Opens in a new window] ,
Rio Baidya ,
Nicholas Hutchins  and
Ivan Marusic
Charitha M. de Silva*
Affiliation:
Department of Mechanical Engineering, The University of Melbourne, Victoria 3010, Australia
Kevin Kevin
Affiliation:
Department of Mechanical Engineering, The University of Melbourne, Victoria 3010, Australia
Rio Baidya
Affiliation:
Department of Mechanical Engineering, The University of Melbourne, Victoria 3010, Australia
Nicholas Hutchins
Affiliation:
Department of Mechanical Engineering, The University of Melbourne, Victoria 3010, Australia
Ivan Marusic
Affiliation:
Department of Mechanical Engineering, The University of Melbourne, Victoria 3010, Australia
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The spatial signature of spanwise velocity coherence in turbulent boundary layers has been studied using a series of unique large-field-of-view multicamera particle image velocimetry experiments, which were configured to capture streamwise/spanwise slices of the boundary layer in both the logarithmic and the wake regions. The friction Reynolds number of 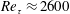$Re_{\unicode[STIX]{x1D70F}}\approx 2600$ was chosen to nominally match the simulation of Sillero et al. (Phys. Fluids, vol. 26 (10), 2014, 105109), who had previously reported oblique features of the spanwise coherence at the top edge of the boundary layer based on the sign of the spanwise velocity, and here we find consistent observations from experiments. In this work, we show that these oblique features in the spanwise coherence relate to the intermittent turbulent bulges at the edge of the layer, and thus the geometry of the turbulent/non-turbulent interface, with the clear appearance of two counter-oriented oblique features. Further, these features are shown to be also present in the logarithmic region once the velocity fields are deconstructed based on the sign of both the spanwise and the streamwise velocity, suggesting that the often-reported meandering of the streamwise-velocity coherence in the logarithmic region is associated with a more obvious diagonal pattern in the spanwise velocity coherence. Moreover, even though a purely visual inspection of the obliqueness in the spanwise coherence may suggest that it extends over a very large spatial extent (beyond many boundary layer thicknesses), through a conditional analysis, we show that this coherence is limited to distances nominally less than two boundary layer thicknesses. Interpretation of these findings is aided by employing synthetic velocity fields of a boundary layer constructed using the attached eddy model, where the range of eddy sizes can be prescribed. Comparisons between the model, which employs an array of self-similar packet-like eddies that are randomly distributed over the plane of the wall, and the experimental velocity fields reveal a good degree of agreement, with both exhibiting oblique features in the spanwise coherence over comparable spatial extents. These findings suggest that the oblique features in the spanwise coherence are likely to be associated with similar structures to those used in the model, providing one possible underpinning structural composition that leads to this behaviour. Further, these features appear to be limited in spatial extent to only the order of the large-scale motions in the flow.

JFM classification

Boundary Layers: Boundary layer structure Turbulent Flows: Turbulent boundary layers Turbulent Flows: Turbulent Flows
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 847 , 25 July 2018 , pp. 161 - 185
Check for updates
Copyright
© 2018 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Adrian, R. J. 2007 Hairpin vortex organization in wall turbulence. Phys. Fluids 19 (4), 041301.Google Scholar
Adrian, R. J., Meinhart, C. D. & Tomkins, C. D. 2000 Vortex organization in the outer region of the turbulent boundary layer. J. Fluid Mech. 422, 1–54.Google Scholar
Anand, R. K., Boersma, B. J. & Agrawal, A. 2009 Detection of turbulent/non-turbulent interface for an axisymmetric turbulent jet: evaluation of known criteria and proposal of a new criterion. Exp. Fluids 47 (6), 995–1007.Google Scholar
Baidya, R., Philip, J., Monty, J. P., Hutchins, N. & Marusic, I. 2014 Comparisons of turbulence stresses from experiments against the attached eddy hypothesis in boundary layers. In Proc. 19th Aust. Fluid Mech. Conf, Australian Fluid Mechanics Society.Google Scholar
Balakumar, B. J. & Adrian, R. J. 2007 Large- and very-large-scale motions in channel and boundary-layer flows. Phil. Trans. R. Soc. Lond. A 365 (1852), 665–681.Google Scholar
Bisset, D. K., Hunt, J. C. R. & Rogers, M. M. 2002 The turbulent/non-turbulent interface bounding a far wake. J. Fluid Mech. 451, 383–410.Google Scholar
Buschmann, M. H., Indinger, T. & Gad-el-Hak, M. 2009 Near-wall behavior of turbulent wall-bounded flows. Intl J. Heat Fluid Flow 30 (5), 993–1006.Google Scholar
Chauhan, K., Philip, J. & Marusic, I. 2014 Scaling of the turbulent/non-turbulent interface in boundary layers. J. Fluid Mech. 751, 298–328.Google Scholar
Chauhan, K. A., Monkewitz, P. A. & Nagib, H. M. 2009 Criteria for assessing experiments in zero pressure gradient boundary layers. Fluid Dyn. Res. 41 (2), 021404.Google Scholar
Coles, D. 1965 Transition in circular Couette flow. J. Fluid Mech. 21 (3), 385–425.CrossRefGoogle Scholar
Delo, C. J., Kelso, R. M. & Smits, A. J. 2004 Three-dimensional structure of a low-Reynolds-number turbulent boundary layer. J. Fluid Mech. 512, 47–83.Google Scholar
Duguet, Y. & Schlatter, P. 2013 Oblique laminar–turbulent interfaces in plane shear flows. Phys. Rev. Lett. 110 (3), 034502.CrossRefGoogle ScholarPubMed
Elsinga, G. E., Adrian, R. J., Van Oudheusden, B. W. & Scarano, F. 2010 Three-dimensional vortex organization in a high-Reynolds-number supersonic turbulent boundary layer. J. Fluid Mech. 644, 35–60.Google Scholar
Falco, R. E. 1977 Coherent motions in the outer region of turbulent boundary layers. Phys. Fluids 20, S124–S132.CrossRefGoogle Scholar
Flores, O. & Jiménez, J. 2010 Hierarchy of minimal flow units in the logarithmic layer. Phys. Fluids 22 (7), 071704.Google Scholar
Ganapathisubramani, B., Longmire, E. K. & Marusic, I. 2003 Characteristics of vortex packets in turbulent boundary layers. J. Fluid Mech. 478, 35–46.Google Scholar
Herpin, S., Stanislas, M., Foucaut, J. M. & Coudert, S. 2013 Influence of the Reynolds number on the vortical structures in the logarithmic region of turbulent boundary layers. J. Fluid Mech. 716, 5–50.Google Scholar
Heskestad, G. 1965 Hot-wire measurements in a plane turbulent jet. Trans. ASME J. Appl. Mech. 32 (4), 721–734.Google Scholar
Hutchins, N., Hambleton, W. T. & Marusic, I. 2005 Inclined cross-stream stereo particle image velocimetry measurements in turbulent boundary layers. J. Fluid Mech. 541, 21–54.Google Scholar
Hutchins, N. & Marusic, I. 2007 Evidence of very long meandering features in the logarithmic region of turbulent boundary layers. J. Fluid Mech. 579, 1–28.Google Scholar
Hwang, Y. & Cossu, C. 2010 Self-sustained process at large scales in turbulent channel flow. Phys. Rev. Lett. 105 (4), 044505.CrossRefGoogle ScholarPubMed
Jeong, J., Hussain, F., Schoppa, W. & Kim, J. 1997 Coherent structures near the wall in a turbulent channel flow. J. Fluid Mech. 332, 185–214.Google Scholar
Jiménez, J., Hoyas, S., Simens, M. P. & Mizuno, Y. 2010 Turbulent boundary layers and channels at moderate Reynolds numbers. J. Fluid Mech. 657, 335–360.Google Scholar
Jolliffe, I. T. 1986 Principal component analysis and factor analysis. In Principal Component Analysis, pp. 115–128. Springer.Google Scholar
Kwon, Y. S., Hutchins, N. & Monty, J. P. 2016 On the use of the Reynolds decomposition in the intermittent region of turbulent boundary layers. J. Fluid Mech. 794, 5–16.Google Scholar
Lee, J., Lee, J. H., Choi, J. I. & Sung, H. J. 2014 Spatial organization of large- and very-large-scale motions in a turbulent channel flow. J. Fluid Mech. 749, 818–840.Google Scholar
Lee, J. H. & Sung, H. J. 2011 Very-large-scale motions in a turbulent boundary layer. J. Fluid Mech. 673, 80–120.Google Scholar
Lozano-Durán, A. & Jiménez, J. 2014 Time-resolved evolution of coherent structures in turbulent channels: characterization of eddies and cascades. J. Fluid Mech. 759, 432–471.Google Scholar
Marusic, I. 2001 On the role of large-scale structures in wall turbulence. Phys. Fluids 13, 735–743.Google Scholar
Marusic, I. & Adrian, R. J. 2012 The eddies and scales of wall turbulence. In Ten Chapters in Turbulence (ed. Davidson, P. A., Yukio, K. & Sreenivasan, K. R.). Cambridge University Press.Google Scholar
Marusic, I. & Heuer, W. D. 2007 Reynolds number invariance of the structure inclination angle in wall turbulence. Phys. Rev. Lett. 99 (11), 114504.CrossRefGoogle ScholarPubMed
Marusic, I., Monty, J. P., Hultmark, M. & Smits, A. J. 2013 On the logarithmic region in wall turbulence. J. Fluid Mech. 716, R3.Google Scholar
Marusic, I. & Perry, A. E. 1995 A wall-wake model for the turbulence structure of boundary layers. Part 2. Further experimental support. J. Fluid Mech. 298, 389–407.CrossRefGoogle Scholar
Mathew, J. & Basu, A. J. 2002 Some characteristics of entrainment at a cylindrical turbulence boundary. Phys. Fluids 14 (7), 2065–2072.Google Scholar
Mathis, R., Hutchins, N. & Marusic, I. 2009 Large-scale amplitude modulation of the small-scale structures in turbulent boundary layers. J. Fluid Mech. 628, 311–337.Google Scholar
Meinhart, C. D. & Adrian, R. J. 1995 On the existence of uniform momentum zones in a turbulent boundary layer. Phys. Fluids 7, 694.Google Scholar
Monty, J. P., Hutchins, N., Ng, H. C. H., Marusic, I. & Chong, M. S. 2009 A comparison of turbulent pipe, channel and boundary layer flows. J. Fluid Mech. 632, 431–442.Google Scholar
Nickels, T. B., Marusic, I., Hafez, S. & Chong, M. S. 2005 Evidence of the k -1 law in a high-Reynolds-number turbulent boundary layer. Phy. Rev. Lett. 95 (7), 074501.Google Scholar
Panton, R. L. 2001 Overview of the self-sustaining mechanisms of wall turbulence. Prog. Aerosp. Sci. 37 (4), 341–383.Google Scholar
Perry, A. E. & Chong, M. S. 1982 On the mechanism of wall turbulence. J. Fluid Mech. 119, 106–121.Google Scholar
Perry, A. E., Henbest, S. M. & Chong, M. 1986 A theoretical and experimental study of wall turbulence. J. Fluid Mech. 165, 163–199.Google Scholar
Perry, A. E. & Marusic, I. 1995 A wall-wake model for the turbulence structure of boundary layers. Part 1. Extension of the attached eddy hypothesis. J. Fluid Mech. 298, 361–388.Google Scholar
Philip, J., Meneveau, C., de Silva, C. M. & Marusic, I. 2014 Multiscale analysis of fluxes at the turbulent/non-turbulent interface in high Reynolds number boundary layers. Phys. Fluids 26 (1), 015105.Google Scholar
Reynolds, O. 1894 On the dynamical theory of incompressible viscous fluids and the determination of the criterion. Proc. R. Soc. Lond. A 56 (336–339), 40–45.Google Scholar
Robinson, S. K. 1991 Coherent motions in the turbulent boundary layer. Annu. Rev. Fluid Mech. 23 (1), 601–639.Google Scholar
Schlatter, P., Li, Q., Örlü, R., Hussain, F. & Henningson, D. S. 2014 On the near-wall vortical structures at moderate Reynolds numbers. Eur. J. Mech. (B/Fluids) 48, 75–93.Google Scholar
Schoppa, W. & Hussain, F. 2002 Coherent structure generation in near-wall turbulence. J. Fluid Mech. 453, 57–108.Google Scholar
Sillero, J. A., Jiménez, J. & Moser, R. D. 2013 One-point statistics for turbulent wall-bounded flows at Reynolds numbers up to 𝛿+ = 2000. Phys. Fluids 25 (10), 105102.Google Scholar
Sillero, J. A., Jiménez, J. & Moser, R. D. 2014 Two-point statistics for turbulent boundary layers and channels at Reynolds numbers up to 𝛿+ = 2000. Phys. Fluids 26 (10), 105109.Google Scholar
de Silva, C. M., Gnanamanickam, E. P., Atkinson, C., Buchmann, N. A., Hutchins, N., Soria, J. & Marusic, I. 2014 High spatial range velocity measurements in a high Reynolds number turbulent boundary layer. Phys. Fluids 26 (2), 025117.Google Scholar
de Silva, C. M., Hutchins, N. & Marusic, I. 2016a Uniform momentum zones in turbulent boundary layers. J. Fluid Mech. 786, 309–331.Google Scholar
de Silva, C. M., Philip, J., Chauhan, K., Meneveau, C. & Marusic, I. 2013 Multiscale geometry and scaling of the turbulent–nonturbulent interface in high Reynolds number boundary layers. Phys. Rev. Lett. 111, 044501.CrossRefGoogle ScholarPubMed
de Silva, C. M., Squire, D. T., Hutchins, N. & Marusic, I. 2015 Towards capturing large scale coherent structures in boundary layers using particle image velocimetry. In Proc. 6th Aust. Conf. Laser Diag. Fluid Mech. Comb., pp. 1–4. University of Melbourne.Google Scholar
de Silva, C. M., Woodcock, J. D., Hutchins, N. & Marusic, I. 2016b Influence of spatial exclusion on the statistical behavior of attached eddies. Phys. Rev. Fluids 1, 022401.Google Scholar
Squire, D. T., Morrill-Winter, C., Hutchins, N., Marusic, I., Schultz, M. P. & Klewicki, J. C. 2016 Smooth- and rough-wall boundary layer structure from high spatial range particle image velocimetry. Phys. Rev. Fluids 1 (6), 064402.Google Scholar
Townsend, A. A. 1976 The Structure of Turbulent Shear Flow, 2nd edn. Cambridge University Press.Google Scholar
Tomkins, C. D. & Adrian, R. J. 2003 Spanwise structure and scale growth in turbulent boundary layers. J. Fluid Mech. 490, 37–74.Google Scholar
Van Atta, C. 1966 Exploratory measurements in spiral turbulence. J. Fluid Mech. 25 (03), 495–512.Google Scholar
Wallace, J. M., Eckelmann, H. & Brodkey, R. S. 1972 The wall region in turbulent shear flow. J. Fluid Mech. 54 (1), 39–48.Google Scholar
Woodcock, J. D. & Marusic, I. 2015 The statistical behaviour of attached eddies. Phys. Fluids 27 (1), 015104.Google Scholar