Hostname: page-component-cd9895bd7-gxg78 Total loading time: 0 Render date: 2024-12-23T09:18:13.309Z Has data issue: false hasContentIssue false
  • English
  • Français

Langmuir turbulence and filament frontogenesis in the oceanic surface boundary layer

Published online by Cambridge University Press:  01 October 2019

Peter P. Sullivan Open the ORCID record for Peter P. Sullivan [Opens in a new window]  and
James C. McWilliams Open the ORCID record for James C. McWilliams [Opens in a new window]
Peter P. Sullivan*
Affiliation:
National Center for Atmospheric Research, Boulder, CO 80307, USA
James C. McWilliams
Affiliation:
Department of Atmospheric and Oceanic Sciences, UCLA, Los Angeles, CA 90095, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Submesoscale currents, small-scale turbulence and surface gravity waves co-exist in the upper ocean and interact in complex ways. To expose the couplings, the frontogenetic life cycle of an idealized cold dense submesoscale filament interacting with upper ocean Langmuir turbulence is investigated in large-eddy simulations (LESs) based on the incompressible wave-averaged equations. The simulations utilize large domains and fine meshes with 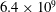$6.4\times 10^{9}$ grid points. Case studies are made with surface winds or surface cooling with waves oriented in across-filament (perpendicular) or down-filament (parallel) directions relative to the two-dimensional filament axis. The currents $u$, $v$ and 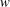$w$ are aligned with the across-filament, down-filament and vertical directions, respectively. Frontogenesis is induced by across-filament Lagrangian secondary circulations in the boundary layer, and it is shown to be strongly impacted by surface waves, in particular the propagation direction relative to the filament axis. In a horizontally heterogeneous boundary layer, surface waves induce both mean and fluctuating Stokes-drift vortex forces that modify a linear, hydrostatic turbulent thermal wind (TTW) approximation for momentum. Down-filament winds and waves are found to be especially impactful, they significantly reduce the peak level of frontogenesis by fragmenting the filament into primary and secondary down-welling sites in a broad frontal zone over a width 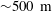${\sim}500~\text{m}$. At peak frontogenesis, opposing down-filament jets 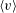$\langle v\rangle$ overlie each other resulting in a vigorous vertical shear layer 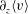$\unicode[STIX]{x2202}_{z}\langle v\rangle$ with large vertical momentum flux 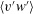$\langle v^{\prime }w^{\prime }\rangle$. Filament arrest is induced by a lateral shear instability that generates horizontal momentum flux 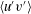$\langle u^{\prime }v^{\prime }\rangle$ at low wavenumbers. The turbulent vertical velocity patterns, indicative of coherent Langmuir cells, change markedly across the horizontal domain with both across-filament and down-filament winds under the action of submesoscale currents.

JFM classification

Geophysical and Geological Flows: Ocean processes Turbulent Flows: Turbulent boundary layers Turbulent Flows: Turbulence simulation
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 879 , 25 November 2019 , pp. 512 - 553
Check for updates
Copyright
© 2019 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Belcher, S. E., Grant, A. A. L. M., Hanley, K. E., Fox-Kemper, B., Van Roekel, L., Sullivan, P. P., Large, W. G., Brown, A., Hines, A., Calvert, D. et al. 2012 A global perspective on Langmuir turbulence in the ocean surface boundary layer. Geophys. Res. Lett. 39, L18605.10.1029/2012GL052932Google Scholar
Craik, A. D. D. & Leibovich, S. 1976 A rational model for Langmuir circulations. J. Fluid Mech. 73, 401–426.Google Scholar
D’Asaro, E., Thomson, J., Shcherbina, A. Y., Harcourt, R. R., Cronin, M. F., Hemer, M. A. & Fox-Kemper, B. 2014 Quantifying upper ocean turbulence driven by surface waves. Geophys. Res. Lett. 41, 1–6.Google Scholar
Deardorff, J. W. 1972 Numerical investigation of neutral and unstable planetary boundary layers. J. Atmos. Sci. 29, 91–115.10.1175/1520-0469(1972)029<0091:NIONAU>2.0.CO;22.0.CO;2>Google Scholar
Edson, J., Crawford, T., Crescenti, J., Farrar, T., French, J., Frew, N., Gerbi, G., Helmis, C., Hristov, T., Khelif, D. et al. 2007 The coupled boundary layers and air–sea transfer experiment in low winds (CBLAST-Low). Bull. Am. Meteorol. Soc. 88, 342–356.Google Scholar
Grant, A. L. M. & Belcher, S. E. 2009 Characteristics of Langmuir turbulence in the ocean mixed layer. J. Phys. Oceanogr. 39, 1871–1887.10.1175/2009JPO4119.1Google Scholar
Gula, J., Molemaker, M. J. & McWilliams, J. C. 2014 Submesoscale cold filaments in the Gulf Stream. J. Phys. Oceanogr. 44, 2617–2643.10.1175/JPO-D-14-0029.1Google Scholar
Hamlington, P. E., Van Roekel, L. P., Fox-Kemper, B., Julien, K. & Chini, G. P. 2014 Langmuir–submesoscale interactions: descriptive analysis of multiscale frontal spindown simulations. J. Phys. Oceanogr. 44, 2249–2272.10.1175/JPO-D-13-0139.1Google Scholar
Haney, S., Fox-Kemper, B., Julien, K. & Webb, A. 2015 Symmetric and geostrophic instabilities in the wave-forced ocean mixed layer. J. Phys. Oceanogr. 45, 3033–3056.10.1175/JPO-D-15-0044.1Google Scholar
Harcourt, R. R. & D’Asaro, E. A. 2008 Large-eddy simulation of Langmuir turbulence in pure wind seas. J. Phys. Oceanogr. 38, 1542–1562.Google Scholar
Holm, D. D. 1996 The ideal Craik-Leibovich equations. Physica D 98, 415–441.Google Scholar
Kaminski, A. K. & Smyth, W. D. 2019 Stratified shear instability in a field of pre-existing turbulence. J. Fluid Mech. 862, 639–658.Google Scholar
Kukulka, T., Plueddemann, A. J. & Sullivan, P. P. 2013 Inhibited upper ocean restratification in nonequilibrium swell conditions. Geophys. Res. Lett. 40, 3672–3676.10.1002/grl.50708Google Scholar
Kukulka, T., Plueddemann, A. J., Trowbridge, J. H. & Sullivan, P. P. 2009 The effect of breaking waves on a coupled model of wind and ocean surface waves: II. Growing seas. Geophys. Res. Lett. 36, L10603.Google Scholar
Lapeyre, G. & Klein, P. 2006 Impact of the small-scale elongated filaments on the oceanic vertical pump. J. Mar. Res. 64, 835–851.10.1357/002224006779698369Google Scholar
Large, W. G., McWilliams, J. C. & Doney, S. C. 1994 Oceanic vertical mixing: A review and a model with a nonlocal boundary layer parameterization. Rev. Geophys. 32, 363–403.10.1029/94RG01872Google Scholar
Large, W. G. & Pond, S. 1981 Open ocean flux measurements in moderate to strong winds. J. Phys. Oceanogr. 11, 324–336.10.1175/1520-0485(1981)011<0324:OOMFMI>2.0.CO;22.0.CO;2>Google Scholar
Leibovich, S. 1983 The form and dynamics of Langmuir circulations. Annu. Rev. Fluid Mech. 15, 391–427.Google Scholar
Li, K., Zhang, Z., Chini, G. & Flierl, G. 2012 Langmuir circulation: An agent for vertical restratification? J. Phys. Oceanogr. 42, 1945–1958.10.1175/JPO-D-11-0225.1Google Scholar
McWilliams, J. C. 2004 Phenomenological hunts in two-dimensional and stably stratified turbulence. In Atmospheric Turbulence and Mesoscale Meteorology (ed. Federovich, E., Rotunno, R. & Stevens, B.), pp. 35–49. Cambridge University Press.Google Scholar
McWilliams, J. C. 2016 Submesoscale currents in the ocean. Proc. R. Soc. Lond. A 472, 1–32.Google Scholar
McWilliams, J. C. 2017 Submesoscale surface fronts and filaments: Secondary circulation, buoyancy flux, and frontogenesis. J. Fluid Mech. 823, 391–432.10.1017/jfm.2017.294Google Scholar
McWilliams, J. C. 2018 Surface wave effects on submesoscale fronts and filaments. J. Fluid Mech. 843, 479–517.Google Scholar
McWilliams, J. C., Colas, F. & Molemaker, M. J. 2009a Cold filamentary intensification and oceanic surface convergence lines. Geophys. Res. Lett. 36, 1–5, L18602.Google Scholar
McWilliams, J. C. & Fox-Kemper, B. 2013 Oceanic wave-balanced surface fronts and filaments. J. Fluid Mech. 730, 464–490.Google Scholar
McWilliams, J. C., Gula, J., Molemaker, M. J., Renault, L. & Shchepetkin, A. F. 2015 Filament frontogenesis by boundary layer turbulence. J. Phys. Oceanogr. 45, 1988–2005.10.1175/JPO-D-14-0211.1Google Scholar
McWilliams, J. C., Huckle, E., Liang, J.-H. & Sullivan, P. P. 2014 Langmuir turbulence in swell. J. Phys. Oceanogr. 44, 870–890.Google Scholar
McWilliams, J. C., Moeng, C.-H. & Sullivan, P. P. 1999 Turbulent fluxes and coherent structures in marine boundary layers: Investigations by large-eddy simulation. In Air–Sea Exchange: Physics, Chemistry, Dynamics, and Statistics (ed. Geernaert, G.), pp. 507–538. Kluwer.10.1007/978-94-015-9291-8_18Google Scholar
McWilliams, J. C., Molemaker, M. J. & Olafsdottir, E. I. 2009b Linear fluctuation growth during frontogenesis. J. Phys. Oceanogr. 39, 3111–3129.10.1175/2009JPO4186.1Google Scholar
McWilliams, J. C., Restrepo, J. R. & Lane, E. M. 2004 An asymptotic theory for the interaction of waves and currents in shallow coastal water. J. Fluid Mech. 511, 135–178.10.1017/S0022112004009358Google Scholar
McWilliams, J. C., Sullivan, P. P. & Moeng, C.-H. 1997 Langmuir turbulence in the ocean. J. Fluid Mech. 334, 1–30.Google Scholar
Moeng, C.-H. 1984 A large-eddy simulation model for the study of planetary boundary-layer turbulence. J. Atmos. Sci. 41, 2052–2062.10.1175/1520-0469(1984)041<2052:ALESMF>2.0.CO;22.0.CO;2>Google Scholar
Moeng, C.-H. & Sullivan, P. P. 2015 Large-eddy simulation. In Encyclopedia of Atmospheric Sciences 2nd Edition (ed. North, G. R., Zhang, F. & Pyle, J.), vol. 4, pp. 232–240. Academic Press.10.1016/B978-0-12-382225-3.00201-2Google Scholar
Pham, H. T. & Sarkar, S. 2018 Ageostrophic secondary circulation at a submesoscale front and formation of gravity currents. J. Phys. Oceanogr. 48, 2507–2529.10.1175/JPO-D-17-0271.1Google Scholar
Polton, J. A., Lewis, D. M. & Belcher, S. E. 2005 The role of wave-induced Coriolis–Stokes forcing on the wind-driven mixed layer. J. Phys. Oceanogr. 35, 444–457.10.1175/JPO2701.1Google Scholar
Pope, S. B. 2000 Turbulent Flows. Cambridge University Press.10.1017/CBO9780511840531Google Scholar
Skyllingstad, E. D. & Samelson, R. M. 2012 Baroclinic frontal instabilities and turbulent mixing in the surface boundary layer. Part I. Unforced simulations. J. Phys. Oceanogr. 42, 1701–1716.10.1175/JPO-D-10-05016.1Google Scholar
Smith, K. M., Hamlington, P. E. & Fox-Kemper, B. 2016 Effects of submesoscale turbulence on ocean tracers. J. Geophys. Res. Oceans 121, 908–933.10.1002/2015JC011089Google Scholar
Sullivan, P. P., Edson, J. B., Hristov, T. & McWilliams, J. C. 2008 Large eddy simulations and observations of atmospheric marine boundary layers above non-equilibrium surface waves. J. Atmos. Sci. 65, 1225–1245.10.1175/2007JAS2427.1Google Scholar
Sullivan, P. P. & McWilliams, J. C. 2010 Dynamics of winds and currents coupled to surface waves. Annu. Rev. Fluid Mech. 42, 19–42.10.1146/annurev-fluid-121108-145541Google Scholar
Sullivan, P. P. & McWilliams, J. C. 2018 Frontogenesis and frontal arrest of a dense filament in the oceanic surface boundary layer. J. Fluid Mech. 837, 341–380.Google Scholar
Sullivan, P. P., McWilliams, J. C. & Melville, W. K. 2007a Catalyzing Craik-Leibovich instabilities by breaking waves. In 5th International Symposium on Environmental Hydraulics, International Association for Hydro-Environmental Engineering and Research.Google Scholar
Sullivan, P. P., McWilliams, J. C. & Melville, W. K. 2007b Surface gravity wave effects in the oceanic boundary layer: Large-eddy simulation with vortex force and stochastic breakers. J. Fluid Mech. 593, 405–452.Google Scholar
Sullivan, P. P., McWilliams, J. C. & Moeng, C.-H. 1994 A subgrid-scale model for large-eddy simulation of planetary boundary-layer flows. Boundary-Layer Meteorol. 71, 247–276.10.1007/BF00713741Google Scholar
Sullivan, P. P., McWilliams, J. C. & Moeng, C.-H. 1996 A grid nesting method for large-eddy simulation of planetary boundary layer flows. Boundary-Layer Meteorol. 80, 167–202.10.1007/BF00119016Google Scholar
Sullivan, P. P. & Patton, E. G. 2011 The effect of mesh resolution on convective boundary-layer statistics and structures generated by large-eddy simulation. J. Atmos. Sci. 68, 2395–2415.10.1175/JAS-D-10-05010.1Google Scholar
Sullivan, P. P., Romero, L., McWilliams, J. C. & Melville, W. K. 2012 Transient evolution of Langmuir turbulence in ocean boundary layers driven by hurricane winds and waves. J. Phys. Oceanogr. 42, 1959–1980.10.1175/JPO-D-12-025.1Google Scholar
Suzuki, N. & Fox-Kemper, B. 2016 Understanding Stokes forces in the wave-averaged equations. J. Geophys. Res. Oceans 121, 3579–3596.Google Scholar
Suzuki, N., Fox-Kemper, B., Hamlington, P. E. & Roekel, L. P. V. 2016 Surface waves affect frontogenesis. J. Geophys. Res. Oceans 121, 3597–3624.10.1002/2015JC011563Google Scholar
Taylor, J. R. & Ferrari, R. 2010 Buoyancy and wind-driven convection at mixed layer density fronts. J. Phys. Oceanogr. 40, 1222–1242.10.1175/2010JPO4365.1Google Scholar
Thomas, L. N., Ferrari, R. & Joyce, T. M. 2013 Symmetric instability in the Gulf Stream. Deep-Sea Res. II 91, 96–110.Google Scholar
Thomas, L. N. & Lee, C. 2005 Intensification of ocean fronts by down-front winds. J. Phys. Oceanogr. 35, 1086–1102.10.1175/JPO2737.1Google Scholar
Van Roekel, L. P., Fox-Kemper, B., Sullivan, P. P., Hamlington, P. E. & Haney, S. R. 2012 The form and orientation of Langmuir cells for misaligned winds and waves. J. Geophys. Res. Oceans 117, 1–22.Google Scholar
Werne, J. & Fritts, D. C. 1999 Stratified shear turbulence: Evolution and statistics. Geophys. Res. Lett. 26, 439–442.10.1029/1999GL900022Google Scholar