Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Zanoun, E.-S.
Kito, M.
and
Egbers, C.
2009.
A Study on Flow Transition and Development in Circular and Rectangular Ducts.
Journal of Fluids Engineering,
Vol. 131,
Issue. 6,
Durst, F.
Haddad, K.
and
Ertunç, Ö.
2009.
Advances in Turbulence XII.
Vol. 132,
Issue. ,
p.
131.
DOU, HUA-SHU
and
KHOO, BOO CHEONG
2010.
CRITERIA OF TURBULENT TRANSITION IN PARALLEL FLOWS.
Modern Physics Letters B,
Vol. 24,
Issue. 13,
p.
1437.
Nishi, Mina
Ertunç, Özgür
and
Delgado, Antonio
2010.
Seventh IUTAM Symposium on Laminar-Turbulent Transition.
Vol. 18,
Issue. ,
p.
537.
DUGUET, Y.
WILLIS, A. P.
and
KERSWELL, R. R.
2010.
Slug genesis in cylindrical pipe flow.
Journal of Fluid Mechanics,
Vol. 663,
Issue. ,
p.
180.
Dou, Hua-Shu
Khoo, Boo Cheong
and
Tsai, Her Mann
2010.
Determining the critical condition for turbulent transition in a full-developed annulus flow.
Journal of Petroleum Science and Engineering,
Vol. 73,
Issue. 1-2,
p.
41.
Duguet, Yoann
Willis, A. P.
and
Kerswell, R. R.
2010.
États limites et bouffées turbulentes en conduite cylindrique.
Mécanique & Industries,
Vol. 11,
Issue. 2,
p.
157.
Dou, Hua-shu
and
Khoo, Boo Cheong
2010.
Energy gradient method for turbulent transition with consideration of effect of disturbance frequency.
Journal of Hydrodynamics,
Vol. 22,
Issue. S1,
p.
23.
KUIK, D. J.
POELMA, C.
and
WESTERWEEL, J.
2010.
Quantitative measurement of the lifetime of localized turbulence in pipe flow.
Journal of Fluid Mechanics,
Vol. 645,
Issue. ,
p.
529.
Barkley, Dwight
2011.
Simplifying the complexity of pipe flow.
Physical Review E,
Vol. 84,
Issue. 1,
Sipos, Maksim
and
Goldenfeld, Nigel
2011.
Directed percolation describes lifetime and growth of turbulent puffs and slugs.
Physical Review E,
Vol. 84,
Issue. 3,
ICHIMIYA, Masashi
FUJIMURA, Hayato
and
TAMATANI, Junji
2011.
Laminar-Turbulent Transition of an Inlet Boundary Layer in a Circular Pipe Induced by Periodic Ejection (Condition for Generating an Isolated Turbulent Patch).
Journal of Fluid Science and Technology,
Vol. 6,
Issue. 6,
p.
902.
Dou, Hua-Shu
and
Khoo, Boo-Cheong
2011.
Theory and Prediction of Turbulent Transition.
International Journal of Fluid Machinery and Systems,
Vol. 4,
Issue. 1,
p.
114.
SAMANTA, DEVRANJAN
DE LOZAR, ALBERTO
and
HOF, BJÖRN
2011.
Experimental investigation of laminar turbulent intermittency in pipe flow.
Journal of Fluid Mechanics,
Vol. 681,
Issue. ,
p.
193.
Dou, Hua-Shu
and
Khoo, Boo Cheong
2011.
Investigation of Turbulent Transition in Plane Couette Flows Using Energy Gradient Method.
Advances in Applied Mathematics and Mechanics,
Vol. 3,
Issue. 2,
p.
165.
Eckhardt, Bruno
2011.
A Critical Point for Turbulence.
Science,
Vol. 333,
Issue. 6039,
p.
165.
Avila, Kerstin
Moxey, David
de Lozar, Alberto
Avila, Marc
Barkley, Dwight
and
Hof, Björn
2011.
The Onset of Turbulence in Pipe Flow.
Science,
Vol. 333,
Issue. 6039,
p.
192.
Barkley, Dwight
2011.
Modeling the transition to turbulence in shear flows.
Journal of Physics: Conference Series,
Vol. 318,
Issue. 3,
p.
032001.
Kurokawa, Junichi
2011.
J-Groove Technique for Suppressing Various Anomalous Flow Phenomena in Turbomachines.
International Journal of Fluid Machinery and Systems,
Vol. 4,
Issue. 1,
p.
1.
Mullin, T.
2011.
Experimental Studies of Transition to Turbulence in a Pipe.
Annual Review of Fluid Mechanics,
Vol. 43,
Issue. 1,
p.
1.
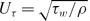 ; τw is the wall shear stress and ρ is the density of the fluid).
; τw is the wall shear stress and ρ is the density of the fluid).