Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Tumuklu, Ozgur
Levin, Deborah A.
and
Theofilis, Vassilis
2018.
Investigation of unsteady, hypersonic, laminar separated flows over a double cone geometry using a kinetic approach.
Physics of Fluids,
Vol. 30,
Issue. 4,
Prakash, R.
Gai, S.
and
O’Byrne, S.
2018.
A direct simulation Monte Carlo study of hypersonic leading-edge separation with rarefaction effects.
Physics of Fluids,
Vol. 30,
Issue. 6,
Bhide, Paritosh M.
Singh, Narendra
Schwartzentruber, Thomas E.
Nompelis, Ioannis
and
Candler, Graham V.
2018.
Slip effects in near continuum hypersonic flow over canonical geometries.
Xiao, H.
and
He, Q.J.
2018.
Aero-heating in hypersonic continuum and rarefied gas flows.
Aerospace Science and Technology,
Vol. 82-83,
Issue. ,
p.
566.
Khraibut, Amna
Gai, S. L.
and
Neely, A. J.
2019.
Numerical study of bluntness effects on laminar leading edge separation in hypersonic flow.
Journal of Fluid Mechanics,
Vol. 878,
Issue. ,
p.
386.
Tumuklu, Ozgur
Levin, Deborah A.
and
Theofilis, Vassilis
2019.
Kinetic modeling of unsteady hypersonic flows over a tick geometry.
Physics of Fluids,
Vol. 31,
Issue. 5,
Gai, Sudhir L.
and
Khraibut, Amna
2019.
Hypersonic compression corner flow with large separated regions.
Journal of Fluid Mechanics,
Vol. 877,
Issue. ,
p.
471.
Gai, S. L.
Prakash, R.
Khraibut, A.
Le Page, L.
and
O’Byrne, S.
2019.
Large scale hypersonic separated flows at moderate Reynolds numbers and moderate density.
Vol. 2132,
Issue. ,
p.
100005.
Le Page, Laurent M.
Barrett, Matthew
O’Byrne, Sean
and
Gai, Sudhir L.
2019.
Rotational temperature imaging of a leading-edge separation in hypervelocity flow.
Vol. 2132,
Issue. ,
p.
110001.
Prakash, R.
Le Page, L. M.
McQuellin, L. P.
Gai, S. L.
and
O’Byrne, S.
2019.
Direct simulation Monte Carlo computations and experiments on leading-edge separation in rarefied hypersonic flow.
Journal of Fluid Mechanics,
Vol. 879,
Issue. ,
p.
633.
Hao, Jiaao
and
Wen, Chih-Yung
2020.
Hypersonic flow over spherically blunted double cones.
Journal of Fluid Mechanics,
Vol. 896,
Issue. ,
Le Page, Laurent M.
Barrett, Matthew
O’Byrne, Sean
and
Gai, Sudhir L.
2020.
Laser-induced fluorescence velocimetry for a hypersonic leading-edge separation.
Physics of Fluids,
Vol. 32,
Issue. 3,
Exposito Brioso, Diego
Laxman Gai, Sudhir
and
Neely, Andrew J.
2020.
Wall Temperature Effects on Two-dimensional Hypersonic Laminar Separation.
Exposito, D.
Gai, S.L.
and
Neely, A.J.
2021.
Wall temperature and bluntness effects on hypersonic laminar separation at a compression corner.
Journal of Fluid Mechanics,
Vol. 922,
Issue. ,
Hao, Jiaao
Cao, Shibin
Wen, Chih-Yung
and
Olivier, Herbert
2021.
Occurrence of global instability in hypersonic compression corner flow.
Journal of Fluid Mechanics,
Vol. 919,
Issue. ,
Hao, Jiaao
Fan, Jianhui
Cao, Shibin
and
Wen, Chih-Yung
2022.
Three-dimensionality of hypersonic laminar flow over a double cone.
Journal of Fluid Mechanics,
Vol. 935,
Issue. ,
Srinath, L.
Sriram, R.
Akhilesh, P.
and
Jagadeesh, G.
2022.
Shock-induced leading-edge separation in hypersonic flows.
Journal of Fluid Mechanics,
Vol. 947,
Issue. ,
Khraibut, A.
and
Gai, S.L.
2022.
Bluntness and incidence effects in hypersonic flows with large separated regions.
Journal of Fluid Mechanics,
Vol. 947,
Issue. ,
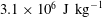 $3.1\times 10^{6}~\text{J}~\text{kg}^{-1}$ with a unit Reynolds number of
$3.1\times 10^{6}~\text{J}~\text{kg}^{-1}$ with a unit Reynolds number of 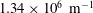 $1.34\times 10^{6}~\text{ m}^{-1}$ and a Mach number of 9.66 was considered. The resulting separated flow is analysed in the context of viscous–inviscid interaction and interpreted in terms of ‘triple-deck’ concepts. Particular emphasis is given to wall temperature effects. The effects of strong to moderate wall cooling on flow in the separated region as well as on processes of separation, reattachment and separation length, are highlighted. The numerical simulations have also shown the existence of a secondary eddy embedded within the primary recirculation region, with its size, shape and position, being strongly affected by the wall temperature.
$1.34\times 10^{6}~\text{ m}^{-1}$ and a Mach number of 9.66 was considered. The resulting separated flow is analysed in the context of viscous–inviscid interaction and interpreted in terms of ‘triple-deck’ concepts. Particular emphasis is given to wall temperature effects. The effects of strong to moderate wall cooling on flow in the separated region as well as on processes of separation, reattachment and separation length, are highlighted. The numerical simulations have also shown the existence of a secondary eddy embedded within the primary recirculation region, with its size, shape and position, being strongly affected by the wall temperature.


