Hostname: page-component-78c5997874-j824f Total loading time: 0 Render date: 2024-11-04T19:42:19.178Z Has data issue: false hasContentIssue false
  • English
  • Français

A Lagrangian study of turbulent mixing: forward and backward dispersion of molecular trajectories in isotropic turbulence

Published online by Cambridge University Press:  23 June 2016

D. Buaria ,
P. K. Yeung  and
B. L. Sawford
D. Buaria
Affiliation:
School of Aerospace Engineering, Georgia Institute of Technology, Atlanta, GA 30332, USA
P. K. Yeung*
Affiliation:
School of Aerospace Engineering, Georgia Institute of Technology, Atlanta, GA 30332, USA School of Mechanical Engineering, Georgia Institute of Technology, Atlanta, GA 30332, USA
B. L. Sawford
Affiliation:
Department of Mechanical and Aerospace Engineering, Monash University, Clayton, VIC 3800, Australia
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Statistics of the trajectories of molecules diffusing via Brownian motion in a turbulent flow are extracted from simulations of stationary isotropic turbulence, using a postprocessing approach applicable in both forward and backward reference frames. Detailed results are obtained for Schmidt numbers (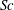$Sc$) from 0.001 to 1000 at Taylor-scale Reynolds numbers up to 1000. The statistics of displacements of single molecules compare well with the earlier theoretical work of Saffman (J. Fluid Mech. vol. 8, 1960, pp. 273–283) except for the scaling of the integral time scale of the fluid velocity following the molecular trajectories. For molecular pairs we extend Saffman’s theory to include pairs of small but finite initial separation, which is in excellent agreement with numerical results provided that data are collected at sufficiently small times. At intermediate times the separation statistics of molecular pairs exhibit a more robust Richardson scaling behaviour than for the fluid particles. The forward scaling constant is very close to 0.55, whereas the backward constant is approximately 1.53–1.57, with a weak Schmidt number dependence, although no scaling exists if 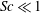$Sc\ll 1$ at the Reynolds numbers presently accessible. An important innovation in this work is to demonstrate explicitly the practical utility of a Lagrangian description of turbulent mixing, where molecular displacements and separations in the limit of small backward initial separation can be used to calculate the evolution of scalar fluctuations resulting from a known source function in space. Lagrangian calculations of the production and dissipation rates of the scalar fluctuations are shown to agree very well with Eulerian results for the case of passive scalars driven by a uniform mean gradient. Although the Eulerian–Lagrangian comparisons are made only for 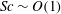$Sc\sim O(1)$, the Lagrangian approach is more easily extended to both very low and very high Schmidt numbers. The well-known scalar dissipation anomaly is accordingly also addressed in a Lagrangian context.

JFM classification

Turbulent Flows: Turbulence simulation Turbulent Flows: Turbulence theory Mixing: Turbulent mixing
Type
Papers
Information
Journal of Fluid Mechanics , Volume 799 , 25 July 2016 , pp. 352 - 382
Check for updates
Copyright
© 2016 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Batchelor, G. K. 1959 Small-scale variation of convected quantities like temperature in turbulent fluid. 1. General discussion and the case of small conductivity. J. Fluid Mech. 5, 113–133.CrossRefGoogle Scholar
Batchelor, G. K., Howells, I. D. & Townsend, A. A. 1959 Small-scale variation of convected quantities like temperature in turbulent fluid. 2. The case of large conductivity. J. Fluid Mech. 5, 134–139.CrossRefGoogle Scholar
Benveniste, D. & Drivas, T. D. 2014 Asymptotic results for backwards two-particle dispersion in turbulent flow. Phys. Rev. E 89, 041003.CrossRefGoogle ScholarPubMed
Berg, J., Luthi, B., Mann, J. & Ott, S. 2006 Backwards and forwards relative dispersion in turbulent flow: an experimental investigation. Phys. Rev. E 74, 016304.CrossRefGoogle ScholarPubMed
Bernard, D., Gawedzki, K. & Kupiainen, A. 1998 Slow modes in passive advection. J. Stat. Phys. 90, 519–569.CrossRefGoogle Scholar
Borgas, M. S., Sawford, B. L., Xu, S., Donzis, D. A. & Yeung, P. K. 2004 High Schmidt number scalars in turbulence: structure functions and Lagrangian theory. Phys. Fluids 16, 3888–3899.CrossRefGoogle Scholar
Bragg, A. D., Ireland, P. J. & Collins, L. R. 2016 Forward and backward in time dispersion of fluid and inertial particles in isotropic turbulence. Phys. Fluids 28, 013305.CrossRefGoogle Scholar
Buaria, D., Sawford, B. L. & Yeung, P. K. 2015 Characteristics of backward and forward two-particle relative dispersion in turbulence at different Reynolds numbers. Phys. Fluids 27, 105101.CrossRefGoogle Scholar
Donzis, D. A., Sreenivasan, K. R. & Yeung, P. K. 2005 Scalar dissipation rate and dissipative anomaly in isotropic turbulence. J. Fluid Mech. 532, 199–216.CrossRefGoogle Scholar
Donzis, D. A., Sreenivasan, K. R. & Yeung, P. K. 2010 The Batchelor spectrum for mixing of passive scalars in isotropic turbulence. Flow Turbul. Combust. 85, 549–566.CrossRefGoogle Scholar
Donzis, D. A. & Yeung, P. K. 2010 Resolution effects and scaling in numerical simulations of passive scalar mixing in turbulence. Physica D 239, 1278–1287.CrossRefGoogle Scholar
Durbin, P. A. 1980 A stochastic model of 2-particle dispersion and concentration fluctuations in homogeneous turbulence. J. Fluid Mech. 100, 279–302.CrossRefGoogle Scholar
Eswaran, V. & Pope, S. B. 1988 An examination of forcing in direct numerical simulations of turbulence. Comput. Fluids 16, 257–278.CrossRefGoogle Scholar
Eyink, G. 2011 Stochastic flux freezing and magnetic dynamo. Phys. Rev. E 83, 056405.CrossRefGoogle ScholarPubMed
Eyink, G. & Benveniste, D. 2013 Diffusion approximation in turbulent two-particle dispersion. Phys. Rev. E 88, 041001(R).CrossRefGoogle ScholarPubMed
Gardiner, C. 1983 Handbook of Stochastic Methods for Physics: Chemistry and the Natural Sciences. Springer.CrossRefGoogle Scholar
Gotoh, T. & Yeung, P. K. 2013 Passive scalar transport in turbulence: a computational perspective. In Ten Chapters in Turbulence (ed. Davidson, P. A., Kaneda, Y. & Sreenivasan, K. R.), Cambridge University Press.Google Scholar
Jucha, J., Xu, H., Pumir, A. & Bodenschatz, E. 2014 Time-reversal-symmetry breaking in turbulence. Phys. Rev. Lett. 113, 054501.CrossRefGoogle ScholarPubMed
Kerr, R. M. 1985 Higher-order derivative correlations and the alignment of small-scale structures in isotropic numerical turbulence. J. Fluid Mech. 153, 31–58.CrossRefGoogle Scholar
Kloeden, P. E. & Platen, E. 1992 Numerical Solution of Stochastic Differential Equations. Springer.CrossRefGoogle Scholar
Monin, A. S. & Yaglom, A. M. 1971 Statistical Fluid Mechanics, vol. 1. MIT Press.Google Scholar
Overholt, M. R. & Pope, S. B. 1996 Direct numerical simulation of a passive scalar with imposed mean gradient in isotropic turbulence. Phys. Fluids 8, 3128–3148.CrossRefGoogle Scholar
Papavassiliou, D. V. & Hanratty, T. J. 1995 Synthesis of temperature fields in terms of the behavior of instantaneous wall sources. In Proceedings of 10th Symposium on Turbulent Shear Flows, pp. 31–19–31–24.Google Scholar
Pope, S. B. 1994 Lagrangian pdf methods for turbulent flows. Annu. Rev. Fluid Mech. 26, 23–63.CrossRefGoogle Scholar
Pope, S. B. 1998 The vanishing effect of molecular diffusivity on turbulent dispersion: implications for turublent mixing and scalar flux. J. Fluid Mech. 359, 299–312.CrossRefGoogle Scholar
Pope, S. B. 2000 Turbulent Flows. Cambridge University Press.CrossRefGoogle Scholar
Richardson, L. F. 1926 Atmospheric diffusion shown on a distance neighbour graph. Proc. R. Soc. Lond. A 110, 709–737.Google Scholar
Saffman, P. G. 1960 On the effect of the molecular diffusivity in turbulent diffusion. J. Fluid Mech. 8, 273–283.CrossRefGoogle Scholar
Sawford, B. L. & Hunt, J. C. R. 1986 Effects of turbulence structure, molecular diffusion and source size on scalar fluctuations in homogeneous turbulence. J. Fluid Mech. 165, 373–400.CrossRefGoogle Scholar
Sawford, B. L. & Pinton, J.-F. 2013 A Lagrangian view of turbulent dispersion and mixing. In Ten Chapters in Turbulence (ed. Davidson, P. A., Kaneda, Y. & Sreenivasan, K. R.), Cambridge University Press.Google Scholar
Sawford, B. L., Yeung, P. K. & Borgas, M. S. 2005 Comparsion of backwards and forwards relative dispersion in turbulence. Phys. Fluids 17, 095109.CrossRefGoogle Scholar
Sawford, B. L., Yeung, P. K. & Hackl, J. F. 2008 Reynolds number dependence of relative dispersion statistics in isotropic turbulence. Phys. Fluids 20, 065111.CrossRefGoogle Scholar
Srinivasan, C. & Papavassiliou, D. V. 2012 Comparsion of backwards and forwards scalar relative dispersion in turbulent shear flow. Intl J. Heat Mass Transfer 55, 5650–5664.CrossRefGoogle Scholar
Taylor, G. I. 1921 Diffusion by continuous movements. Proc. Lond. Math. Soc. 20, 196–202.Google Scholar
Thomson, D. J. 1990 A stochastic model for the motion of particle pairs in isotropic high-Reynolds-number turbulence, and its application to the problem of concentration variance. J. Fluid Mech. 210, 113–153.CrossRefGoogle Scholar
Thomson, D. J. 2003 Dispersion of particle pairs and decay of scalar fields in isotropic turbulence. Phys. Fluids 15, 801–813.CrossRefGoogle Scholar
Toschi, F. & Bodenschatz, E. 2009 Lagrangian properties of particles in turbulence. Annu. Rev. Fluid Mech. 41, 375–404.CrossRefGoogle Scholar
Warhaft, Z 2000 Passive scalars in turbulent flows. Annu. Rev. Fluid Mech. 32, 203–240.CrossRefGoogle Scholar
Watanabe, T. & Gotoh, T. 2006 Intermittency in passive scalar turbulence under the uniform mean scalar gradient. Phys. Fluids 18, 058105.CrossRefGoogle Scholar
Yeung, P. K. 1994 Direct numerical simulation of two-particle relative diffusion in isotropic turbulence. Phys. Fluids 6, 3416–3428.CrossRefGoogle Scholar
Yeung, P. K. 2002 Lagrangian investigations of turbulence. Annu. Rev. Fluid Mech. 34, 115–142.CrossRefGoogle Scholar
Yeung, P. K. & Pope, S. B. 1988 An algorithm for tracking fluid particles in numerical simulations of homogeneous turbulence. J. Comput. Phys. 79, 373–416.CrossRefGoogle Scholar
Yeung, P. K., Pope, S. B., Lamorgese, A. G. & Donzis, D. A. 2006 Acceleration and dissipation statistics of numerically simulated isotropic turbulence. Phys. Fluids 18, 065103.CrossRefGoogle Scholar
Yeung, P. K. & Sreenivasan, K. R. 2014 Direct numerical simulation of turbulent mixing at very low Schmidt number with a uniform mean gradient. Phys. Fluids 26, 015107.CrossRefGoogle Scholar
Yeung, P. K., Xu, S. & Sreenivasan, K. R. 2002 Schmidt number effects on turbulent transport with uniform mean scalar gradient. Phys. Fluids 14, 4178–4191.CrossRefGoogle Scholar