Hostname: page-component-78c5997874-dh8gc Total loading time: 0 Render date: 2024-11-04T21:53:38.792Z Has data issue: false hasContentIssue false
  • English
  • Français

A Lagrangian fluctuation–dissipation relation for scalar turbulence. Part III. Turbulent Rayleigh–Bénard convection

Published online by Cambridge University Press:  12 December 2017

Gregory L. Eyink  and
Theodore D. Drivas Open the ORCID record for Theodore D. Drivas [Opens in a new window]
Gregory L. Eyink
Affiliation:
Department of Applied Mathematics and Statistics, The Johns Hopkins University, Baltimore, MD 21218, USA Department of Physics and Astronomy, The Johns Hopkins University, Baltimore, MD 21218, USA
Theodore D. Drivas*
Affiliation:
Department of Applied Mathematics and Statistics, The Johns Hopkins University, Baltimore, MD 21218, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

A Lagrangian fluctuation–dissipation relation has been derived in a previous work to describe the dissipation rate of advected scalars, both passive and active, in wall-bounded flows. We apply this relation here to develop a Lagrangian description of thermal dissipation in turbulent Rayleigh–Bénard convection in a right-cylindrical cell of arbitrary cross-section, with either imposed temperature difference or imposed heat flux at the top and bottom walls. We obtain an exact relation between the steady-state thermal dissipation rate and the time 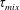$\unicode[STIX]{x1D70F}_{mix}$ for passive tracer particles released at the top or bottom wall to mix to their final uniform value near those walls. We show that an ‘ultimate regime’ with the Nusselt number scaling predicted by Spiegel (Annu. Rev. Astron., vol. 9, 1971, p. 323) or, with a log correction, by Kraichnan (Phys. Fluids, vol. 5 (11), 1962, pp. 1374–1389) will occur at high Rayleigh numbers, unless this near-wall mixing time is asymptotically much longer than the free-fall time 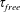$\unicode[STIX]{x1D70F}_{free}$. Precisely, we show that 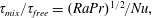$\unicode[STIX]{x1D70F}_{mix}/\unicode[STIX]{x1D70F}_{free}=(RaPr)^{1/2}/Nu,$ with 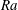$Ra$ the Rayleigh number, 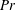$Pr$ the Prandtl number, and 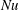$Nu$ the Nusselt number. We suggest a new criterion for an ultimate regime in terms of transition to turbulence of a thermal ‘mixing zone’, which is much wider than the standard thermal boundary layer. Kraichnan–Spiegel scaling may, however, not hold if the intensity and volume of thermal plumes decrease sufficiently rapidly with increasing Rayleigh number. To help resolve this issue, we suggest a program to measure the near-wall mixing time 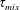$\unicode[STIX]{x1D70F}_{mix}$, which is precisely defined in the paper and which we argue is accessible both by laboratory experiment and by numerical simulation.

JFM classification

Convection: Convection Turbulent Flows: Turbulent convection
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 836 , 10 February 2018 , pp. 560 - 598
Check for updates
Copyright
© 2017 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Ahlers, G., Grossmann, S. & Lohse, D. 2009 Heat transfer and large scale dynamics in turbulent Rayleigh–Bénard convection. Rev. Mod. Phys. 81 (2), 503–537.CrossRefGoogle Scholar
Berg, J., Lüthi, B., Mann, J. & Ott, S. 2006 Backwards and forwards relative dispersion in turbulent flow: an experimental investigation. Phys. Rev. E 74, 016304.Google Scholar
Bergé, P. & Dubois, M. 1984 Rayleigh–Bénard convection. Contemp. Phys. 25 (6), 535–582.Google Scholar
Buaria, D., Yeung, P. K. & Sawford, B. L. 2016 A Lagrangian study of turbulent mixing: forward and backward dispersion of molecular trajectories in isotropic turbulence. J. Fluid Mech. 799, 352–382.CrossRefGoogle Scholar
Calzavarini, E., Doering, C. R., Gibbon, J. D., Lohse, D., Tanabe, A. & Toschi, F. 2006 Exponentially growing solutions in homogeneous Rayleigh–Bénard convection. Phys. Rev. E 73 (3), 035301.Google Scholar
Castaing, B., Gunaratne, G., Kadanoff, L. P., Libchaber, A. & Heslot, F. 1989 Scaling of hard thermal turbulence in Rayleigh–Bénard convection. J. Fluid Mech. 204 (1), 1–30.Google Scholar
Celani, A., Cencini, M., Mazzino, A. & Vergassola, M. 2004 Active and passive fields face to face. New J. Phys. 6 (1), 72.Google Scholar
Chertkov, M. & Lebedev, V. 2003 Decay of scalar turbulence revisited. Phys. Rev. Lett. 90 (3), 034501.CrossRefGoogle ScholarPubMed
Chillà, F. & Schumacher, J. 2012 New perspectives in turbulent Rayleigh–Bénard convection. Eur. Phys. J. E 35 (7), 1–25.Google Scholar
Doering, C. R. & Constantin, P. 1996 Variational bounds on energy dissipation in incompressible flows. Part III. Convection. Phys. Rev. E 53 (6), 5957.Google Scholar
Donzis, D. A., Sreenivasan, K. R. & Yeung, P. K. 2005 Scalar dissipation rate and dissipative anomaly in isotropic turbulence. J. Fluid Mech. 532, 199–216.Google Scholar
Drivas, T. D. & Eyink, G. L. 2017a A Lagrangian fluctuation–dissipation relation for scalar turbulence. Part I. Flows with no bounding walls. J. Fluid Mech. 829, 153–189.CrossRefGoogle Scholar
Drivas, T. D. & Eyink, G. L. 2017b A Lagrangian fluctuation–dissipation relation for scalar turbulence. Part II. Wall-bounded flows. J. Fluid Mech. 829, 236–279.Google Scholar
Emran, M. S. & Schumacher, J. 2008 Fine-scale statistics of temperature and its derivatives in convective turbulence. J. Fluid Mech. 611, 13–34.Google Scholar
Emran, M. S. & Schumacher, J. 2012 Conditional statistics of thermal dissipation rate in turbulent Rayleigh–Bénard convection. Eur. Phys. J. E 35 (10), 1–8.Google Scholar
Eyink, G. L. 2008 Dissipative anomalies in singular Euler flows. Physica D 237 (14), 1956–1968.CrossRefGoogle Scholar
Eyink, G. L. 2011 Stochastic flux freezing and magnetic dynamo. Phys. Rev. E 83 (5), 056405.Google Scholar
Falkovich, G., Gawȩdzki, K. & Vergassola, M. 2001 Particles and fields in fluid turbulence. Rev. Mod. Phys. 73 (4), 913.Google Scholar
Frisch, U. 1986 Fully developed turbulence: where do we stand? In Dynamical Systems: A Renewal of Mechanism: Centennial of Georges David Birkhoff (ed. Diner, S., Fargue, D. & Lochak, G.), pp. 13–28. World Scientific.CrossRefGoogle Scholar
Goluskin, D. 2015 Internally Heated Convection and Rayleigh–Bénard Convection. Springer International Publishing.Google Scholar
Grossmann, S. & Lohse, D. 2000 Scaling in thermal convection: a unifying theory. J. Fluid Mech. 407, 27–56.Google Scholar
Grossmann, S. & Lohse, D. 2001 Thermal convection for large Prandtl numbers. Phys. Rev. Lett. 86 (15), 3316.CrossRefGoogle ScholarPubMed
Grossmann, S. & Lohse, D. 2002 Prandtl and Rayleigh number dependence of the Reynolds number in turbulent thermal convection. Phys. Rev. E 66 (1), 016305.Google Scholar
Grossmann, S. & Lohse, D. 2004 Fluctuations in turbulent Rayleigh–Bénard convection: the role of plumes. Phys. Fluids 16 (12), 4462–4472.Google Scholar
Grossmann, S. & Lohse, D. 2011 Multiple scaling in the ultimate regime of thermal convection. Phys. Fluids 23 (4), 045108.Google Scholar
Grossmann, S. & Lohse, D. 2012 Logarithmic temperature profiles in the ultimate regime of thermal convection. Phys. Fluids 24 (12), 125103.Google Scholar
Hassanzadeh, P., Chini, G. P. & Doering, C. R. 2014 Wall to wall optimal transport. J. Fluid Mech. 751, 627–662.Google Scholar
He, X., Funfschilling, D., Nobach, H., Bodenschatz, E. & Ahlers, G. 2012 Transition to the ultimate state of turbulent Rayleigh–Bénard convection. Phys. Rev. Lett. 108 (2), 024502.CrossRefGoogle Scholar
He, X. & Tong, P. 2009 Measurements of the thermal dissipation field in turbulent Rayleigh–Bénard convection. Phys. Rev. E 79 (2), 026306.Google Scholar
He, X., Tong, P. & Xia, K.-Q. 2007 Measured thermal dissipation field in turbulent Rayleigh–Bénard convection. Phys. Rev. Lett. 98 (14), 144501.Google Scholar
Hewitt, D. R., Neufeld, J. A. & Lister, J. R. 2012 Ultimate regime of high Rayleigh number convection in a porous medium. Phys. Rev. Lett. 108 (22), 224503.Google Scholar
Howard, L. N. 1966 Convection at high Rayleigh number. In Applied Mechanics: Proceedings of the 11th International Congress of Applied Mechanics (ed. Görtler, H.), pp. 1109–1115. Springer.Google Scholar
Huisman, S. G., van der Veen, R. C. A., Sun, C. & Lohse, D. 2014 Multiple states in highly turbulent Taylor–Couette fiow. Nature 5, 3820.Google Scholar
Johnston, H. & Doering, C. R. 2009 Comparison of turbulent thermal convection between conditions of constant temperature and constant flux. Phys. Rev. Lett. 102 (6), 064501.CrossRefGoogle ScholarPubMed
Jucha, J., Xu, H., Pumir, A. & Bodenschatz, E. 2014 Time-reversal-symmetry breaking in turbulence. Phys. Rev. Lett. 113 (5), 054501.Google Scholar
Kraichnan, R. H. 1962 Turbulent thermal convection at arbitrary Prandtl number. Phys. Fluids 5 (11), 1374–1389.Google Scholar
Lebedev, V. V. & Turitsyn, K. S. 2004 Passive scalar evolution in peripheral regions. Phys. Rev. E 69 (3), 036301.Google ScholarPubMed
Lohse, D. & Toschi, F. 2003 Ultimate state of thermal convection. Phys. Rev. Lett. 90 (3), 034502.Google Scholar
Malkus, W. V. R. 1954 The heat transport and spectrum of thermal turbulence. Proc. R. Soc. Lond. A 225 (1161), 196–212.Google Scholar
Niemela, J. J., Skrbek, L., Sreenivasan, K. R. & Donnelly, R. J. 2000 Turbulent convection at very high Rayleigh numbers. Nature 404 (6780), 837–840.Google Scholar
Niemela, J. J. & Sreenivasan, K. R. 2002 Thermal fluctuations and their ordering in turbulent convection. Physica A 315 (1), 203–214.CrossRefGoogle Scholar
Niemela, J. J. & Sreenivasan, K. R. 2003 Confined turbulent convection. J. Fluid Mech. 481, 355–384.Google Scholar
Niemela, J. J. & Sreenivasan, K. R. 2006 Turbulent convection at high Rayleigh numbers and aspect ratio 4. J. Fluid Mech. 557, 411–422.Google Scholar
Otero, J., Dontcheva, L. A., Johnston, H., Worthing, R. A., Kurganov, A., Petrova, G. & Doering, C. R. 2004 High-Rayleigh-number convection in a fluid-saturated porous layer. J. Fluid Mech. 500, 263–281.Google Scholar
Otero, J., Wittenberg, R. W., Worthing, R. A. & Doering, C. R. 2002 Bounds on Rayleigh–Bénard convection with an imposed heat flux. J. Fluid Mech. 473, 191–199.Google Scholar
Priestley, C. H. B. 1959 Turbulent Transfer in the Lower Atmosphere. University of Chicago Press.Google Scholar
Procaccia, I., Ching, E. S. C., Constantin, P., Kadanoff, L. P., Libchaber, A. & Wu, X. 1991 Transitions in convective turbulence: the role of thermal plumes. Phys. Rev. A 44 (12), 8091.Google Scholar
Qiu, X.-L. & Tong, P. 2002 Temperature oscillations in turbulent Rayleigh–Bénard convection. Phys. Rev. E 66 (2), 026308.Google Scholar
Risken, H. 2012 The Fokker–Planck Equation: Methods of Solution and Applications. Springer.Google Scholar
Roche, P.-E., Gauthier, F., Kaiser, R. & Salort, J. 2010 On the triggering of the ultimate regime of convection. New J. Phys. 12 (8), 085014.Google Scholar
Sawford, B. L., Yeung, P. K. & Borgas, M. S. 2005 Comparison of backwards and forwards relative dispersion in turbulence. Phys. Fluids 17, 095109.Google Scholar
Scheel, J. D. & Schumacher, J. 2014 Local boundary layer scales in turbulent Rayleigh–Bénard convection. J. Fluid Mech. 758, 344–373.Google Scholar
Schmidt, L. E., Calzavarini, E., Lohse, D., Toschi, F. & Verzicco, R. 2012 Axially homogeneous Rayleigh–Bénard convection in a cylindrical cell. J. Fluid Mech. 691, 52–68.Google Scholar
Schumacher, J. 2008 Lagrangian dispersion and heat transport in convective turbulence. Phys. Rev. Lett. 100 (13), 134502.Google Scholar
Siggia, E. D. 1994 High Rayleigh number convection. Annu. Rev. Fluid Mech. 26 (1), 137–168.Google Scholar
Souza, A. N.2016 An optimal control approach to bounding transport properties of thermal convection. PhD thesis, University of Michigan, Applied and Interdisciplinary Mathematics.Google Scholar
Spiegel, E. A. 1971 Convection in stars. Part I. Basic Boussinesq convection. Annu. Rev. Astron. 9, 323.Google Scholar
Stevens, R. J. A. M., Lohse, D. & Verzicco, R. 2011 Prandtl and Rayleigh number dependence of heat transport in high Rayleigh number thermal convection. J. Fluid Mech. 688, 31–43.Google Scholar
Tobasco, I. & Doering, C. R. 2017 Optimal wall-to-wall transport by incompressible flows. Phys. Rev. Lett. 118, 264502.Google Scholar
Whitehead, J. P. & Doering, C. R. 2011 Ultimate state of two-dimensional Rayleigh–Bénard convection between free-slip fixed-temperature boundaries. Phys. Rev. Lett. 106 (24), 244501.CrossRefGoogle ScholarPubMed