Hostname: page-component-586b7cd67f-dsjbd Total loading time: 0 Render date: 2024-11-30T15:34:17.310Z Has data issue: false hasContentIssue false
  • English
  • Français

Lagrangian and spectral analysis of the forced flow past a circular cylinder using pulsed tangential jets

Published online by Cambridge University Press:  01 March 2012

T. Jardin  and
Y. Bury
T. Jardin
Affiliation:
Université de Toulouse, ISAE, 31055 Toulouse, France
Y. Bury*
Affiliation:
Université de Toulouse, ISAE, 31055 Toulouse, France
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We numerically investigate the influence of pulsed tangential jets on the flow past a circular cylinder. To this end a spectral-Lagrangian dual approach is used on the basis of time-series data. The analysis reveals that the flow response to unsteady forcing is driven by strong interactions between shear layers and pulsed jets. The latter preferentially lead to either the lock-on regime or the quasi-steady vortex feeding regime whether the excitation frequency is of the order of, or significantly greater than, the frequency of the natural instability. The intensity of the wake vortices is mainly influenced by the momentum coefficient through the introduction of opposite-sign vorticity in the shear layers. This feature is emphasized using a modal-based time reconstruction, i.e. by reconstructing the flow field upon a specific harmonic spectrum associated with a characteristic time scale. The quasi-steady regime exhibits small-scale counter-rotating vortices that circumscribe the separated region. 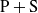In the lock-on regime, atypical wake patterns such as 2P or can be observed, depending on the forcing frequency and the momentum coefficient, highlighting remarkable analogies with oscillating cylinders.

JFM classification

Flow Control: Flow Control Vortex Flows: Vortex Flows Wakes/Jets: Wakes
Type
Papers
Information
Journal of Fluid Mechanics , Volume 696 , 10 April 2012 , pp. 285 - 300
Copyright
Copyright © Cambridge University Press 2012

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1. Bury, Y., Morton, S. A. & Charles, R. 2008 Experimental investigation of the flow field in the close wake of a simplified C-130 shape: a model approach of airflow influence on airdrop. 26th AIAA Applied Aerodynamics Conference, Honolulu, Hawaii, USA.CrossRefGoogle Scholar
2. Choi, H., Jeon, W. P. & Kim, J. 2008 Control of flow over a bluff body. Annu. Rev. Fluid Mech. 40, 113–139.CrossRefGoogle Scholar
3. Gerrard, J. H. 1966 The mechanics of the vortex formation region of vortices behind bluff bodies. J. Fluid Mech. 25, 401–413.CrossRefGoogle Scholar
4. Glezer, A. & Amitay, M. 2002 Synthetic jets. Annu. Rev. Fluid Mech. 34, 503–529.CrossRefGoogle Scholar
5. Glezer, A., Amitay, M. & Honohan, A. M. 2005 Aspect of low- and high-frequency actuation for aerodynamic flow control. AIAA J. 43, 1501–1511.CrossRefGoogle Scholar
6. Henderson, R. D. 1997 Nonlinear dynamics and pattern formation in turbulent wake transition. J. Fluid Mech. 352, 65–112.CrossRefGoogle Scholar
7. Jeon, D. & Gharib, M. 2004 On the relationship between the vortex formation process and cylinder wake vortex patterns. J. Fluid Mech. 519, 161–181.CrossRefGoogle Scholar
8. Jeong, J. & Hussain, F. 1995 On the identification of a vortex. J. Fluid Mech. 285, 69–94.CrossRefGoogle Scholar
9. Jukes, T. N. & Choi, K. S. 2009 Control of unsteady flow separation over a circular cylinder using dielectric-barrier-discharge surface plasma. Phys. Fluids 21, 094106.CrossRefGoogle Scholar
10. Liu, F., Luo, S., Gao, C., Meng, X., Hao, J., Wang, J. & Zhao, Z. 2008 Flow control over a conical forebody using duty-cycled plasma actuators. AIAA J. 46, 2969–2973.CrossRefGoogle Scholar
11. Mezić, I. 2005 Spectral properties of dynamical systems, model reduction and decompositions. Nonlinear Dyn. 41, 309–325.CrossRefGoogle Scholar
12. Morse, T. L. & Williamson, C. H. K. 2009 Prediction of vortex-induced vibration response by employing controlled motion. J. Fluid Mech. 634, 5–39.CrossRefGoogle Scholar
13. Post, M. L. & Corke, T. C. 2004 Separation control on high angle of attack airfoil using plasma actuators. AIAA J. 42, 2177–2184.CrossRefGoogle Scholar
14. Rowley, C. W., Mezić, I., Bagheri, S., Schlatter, P. & Henningson, D. S. 2009 Spectral analysis of nonlinear flows. J. Fluid Mech. 641, 115–127.CrossRefGoogle Scholar
15. Schmid, P. J. 2009 Dynamic mode decomposition of experimental data. 8th International Symposium on Particle Image Velocimetry, Melbourne, Victoria, Australia.Google Scholar
16. Schmid, P. J. 2010 Dynamic mode decomposition of numerical and experimental data. J. Fluid Mech. 656, 5–28.CrossRefGoogle Scholar
17. Schmid, P. J., Meyer, K. E. & Pust, O. 2009 Dynamic mode decomposition and proper orthogonal decomposition of flow in a lid-driven cylindrical cavity. 8th International Symposium on Particle Image Velocimetry, Melbourne, Victoria, Australia.Google Scholar
18. Schmid, P. J. & Sesterhenn, J. 2008 Dynamic mode decomposition of numerical and experimental data. Sixty-First Annual Meeting of the APS Division of Fluid Dynamics, San Antonio, Texas, USA.Google Scholar
19. Schmid, P. J., Violato, D., Pust, O. & Scarano, F. 2010 Decomposition of time-resolved tomographic PIV. In 15th International Symposium on Applications of Laser Techniques to Fluid Mechanics, Lisbon, Portugal.Google Scholar
20. Thomas, F. O., Kozlov, A. & Corke, T. C. 2008 Plasma actuators for cylinder flow control and noise reduction. AIAA J. 46, 1921–1931.CrossRefGoogle Scholar
21. Truesdell, C. 1954 The Kinematics of Vorticity. Science Series, vol. 19 , Indiana University Publications.Google Scholar
22. Williamson, C. H. K. 1996 Vortex dynamics in the cylinder wake. Annu. Rev. Fluid Mech. 28, 477–539.CrossRefGoogle Scholar
23. Williamson, C. H. K. & Roshko, A. 1988 Vortex formation in the wake of an oscillating cylinder. J. Fluids Struct. 2, 355–381.CrossRefGoogle Scholar