Hostname: page-component-78c5997874-m6dg7 Total loading time: 0 Render date: 2024-11-06T04:48:28.951Z Has data issue: false hasContentIssue false
  • English
  • Français

Labyrinthine and secondary wave instabilities of a miscible magnetic fluid drop in a Hele-Shaw cell

Published online by Cambridge University Press:  11 December 2017

Huanhao Li ,
Chun-Yi Kao  and
Chih-Yung Wen Open the ORCID record for Chih-Yung Wen [Opens in a new window]
Huanhao Li
Affiliation:
Department of Mechanical Engineering, The Hong Kong Polytechnic University, Kowloon, Hong Kong Interdisciplinary Division of Biomedical Engineering, The Hong Kong Polytechnic University, Kowloon, Hong Kong
Chun-Yi Kao
Affiliation:
Department of Aeronautics and Astronautics, National Cheng Kung University, Tainan, 701, Taiwan
Chih-Yung Wen*
Affiliation:
Department of Mechanical Engineering, The Hong Kong Polytechnic University, Kowloon, Hong Kong
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

A comprehensive experimental study is presented to analyse the instabilities of a magnetic fluid drop surrounded by miscible fluid confined in a Hele-Shaw cell. The experimental conditions include different magnetic fields (by varying the maximum pre-set magnetic field strengths, 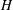$H$, and sweep rates, 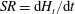$SR=\text{d}H_{t}/\text{d}t$, where 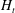$H_{t}$ is the instant magnetic field strength), gap spans, 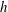$h$, and magnetic fluid samples, and are further coupled into a modified Péclect number 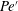$Pe^{\prime }$ to evaluate the instabilities. Two distinct instabilities are induced by the external magnetic fields with different sweep rates: (i) a labyrinthine fingering instability, where small fingerings emerge around the initial circular interface in the early period, and (ii) secondary waves in the later period. Based on 81 sets of experimental conditions, the initial growth rate of the interfacial length, $\unicode[STIX]{x1D6FC}$, of the magnetic drop is found to increase linearly with 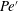$Pe^{\prime }$, indicating that $\unicode[STIX]{x1D6FC}$ is proportional to the square root of the 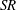$SR$ and 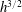$h^{3/2}$ at the onset of the labyrinthine instability. In addition, secondary waves, which are characterised by the dimensionless wavelength 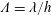$\unicode[STIX]{x1D6EC}=\unicode[STIX]{x1D706}/h$, can only be triggered when the three-dimensional magnetic microconvection is strong enough to make 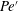$Pe^{\prime }$ exceed a critical value, i.e. 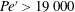$Pe^{\prime }>19\,000$, where 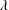$\unicode[STIX]{x1D706}$ is the wavelength of the secondary wave. In this flow regime of high 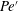$Pe^{\prime }$, the length scale of the secondary wave instability is found to be 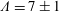$\unicode[STIX]{x1D6EC}=7\pm 1$, corresponding to the Stokes regime; meanwhile, in the flow regime of low 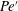$Pe^{\prime }$, the flow corresponds to the Hele-Shaw regime introduced by Fernandez et al. (J. Fluid Mech., vol. 451, 2002, pp. 239–260).

JFM classification

Low-Reynolds-number flows: Hele-Shaw flows Low-Reynolds-number flows: Low-Reynolds-number flows MHD and Electrohydrodynamics: Magnetic fluids
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 836 , 10 February 2018 , pp. 374 - 396
Check for updates
Copyright
© 2017 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

‡

The first and second authors contributed equally to this work.

References

Cēbers, A. & Drikis, I. 1999 Labyrinthine pattern formation in magnetic liquids. In Chapman and Hall CRC Research Notes in Mathematics, pp. 14–38. Chapman and Hall.Google Scholar
Cēbers, A. & Maiorov, M. M. 1980a Magnetostatic instabilities in plane layers of magnetizable fluids. Magnetohydrodynamics 16 (1), 21–27.Google Scholar
Cēbers, A. & Maiorov, M. M. 1980b Structures of interface a bubble and magnetic fluid in a field. Magnetohydrodynamics 16 (3), 231–235.Google Scholar
Chen, C. Y. 2003 Numerical simulations of fingering instabilities in miscible magnetic fluids in a Hele-Shaw cell and the effects of Korteweg stresses. Phys. Fluids 15 (4), 1086–1089.CrossRefGoogle Scholar
Chen, C. Y. & Li, C. S. 2010 Ordered microdroplet formations of thin ferrofluid layer breakups. Phys. Fluids 22 (1), 014105.CrossRefGoogle Scholar
Chen, C. Y. & Liu, Y. C. 2005 Numerical simulations of miscible fluids on a rotating Hele-Shaw cell with effects of Coriolis forces. Intl J. Numer. Meth. Fluids 48 (8), 853–867.Google Scholar
Chen, C. Y., Tsai, W. K. & Miranda, J. A. 2008 Hybrid ferrohydrodynamic instability: coexisting peak and labyrinthine patterns. Phys. Rev. E 77 (5), 056306.Google Scholar
Chen, C. Y. & Wen, C. Y. 2002 Numerical simulations of miscible magnetic flows in a Hele-Shaw cell: radial flows. J. Magn. Magn. Mater. 252, 296–298.Google Scholar
Chen, C. Y. & Wu, H. J. 2005 Numerical simulations of interfacial instabilities on a rotating miscible magnetic droplet with effects of Korteweg stresses. Phys. Fluids 17 (4), 042101.CrossRefGoogle Scholar
Chen, C. Y., Wu, H. J. & Hsu, L. 2005 Numerical simulations of labyrinthine instabilities on a miscible elliptical magnetic droplet. J. Magn. Magn. Mater. 289, 364–366.CrossRefGoogle Scholar
Chen, M. Y., Chen, L. Q., Li, H. & Wen, C. Y. 2017 Labyrinthine instabilities of miscible magnetic fluids in a rotating Hele-Shaw cell. Phys. Fluids 29 (2), 024109.Google Scholar
Dickstein, A. J., Erramilli, S., Goldstein, R. E., Jackson, D. P. & Langer, S. A. 1993 Labyrinthine pattern formation in magnetic fluids. Science 261, 1012–1012.Google Scholar
Ērglis, K., Tatulcenkov, A., Kitenbergs, G., Petrichenko, O., Ergin, F. G., Watz, B. B. & Cēbers, A. 2013 Magnetic field driven micro-convection in the Hele-Shaw cell. J. Fluid Mech. 714, 612–633.Google Scholar
Fernandez, J., Kurowski, P., Limat, L. & Petitjeans, P. 2001 Wavelength selection of fingering instability inside Hele-Shaw cells. Phys. Fluids 13 (11), 3120–3125.Google Scholar
Fernandez, J., Kurowski, P., Petitjeans, P. & Meiburg, E. 2002 Density-driven unstable flows of miscible fluids in a Hele-Shaw cell. J. Fluid Mech. 451, 239–260.Google Scholar
Flament, C., Pacitto, G., Bacri, J. C., Drikis, I. & Cēbers, A. 1998 Viscous fingering in a magnetic fluid. I. Radial Hele-Shaw flow. Phys. Fluids 10 (10), 2464–2472.CrossRefGoogle Scholar
Igonin, M. & Cēbers, A. 2003 Labyrinthine instability of miscible magnetic fluids. Phys. Fluids 15 (6), 1734–1744.CrossRefGoogle Scholar
Jackson, D., Goldstein, R. & Cēbers, A. 1994 Hydrodynamics of fingering instabilities in dipolar fluids. Phys. Rev. E 50 (1), 298–307.Google Scholar
Kitenbergs, G., Tatulcenkovs, A., Ērglis, K., Petrichenko, O., Perzynski, R. & Cēbers, A. 2015 Magnetic field driven micro-convection in the Hele-Shaw cell: the Brinkman model and its comparison with experiment. J. Fluid Mech. 774, 170–191.Google Scholar
Lai, J. C. & Hong, C. Y. 2014 Magnetic-assisted rapid aptamer selection (MARAS) for generating high-affinity DNA aptamer using rotating magnetic fields. ACS Comb. Sci. 16 (7), 321–327.Google Scholar
Lajeunesse, E., Martin, J., Rakotomalala, N. & Salin, D. 1997 3D instability of miscible displacements in a Hele-Shaw cell. Phys. Rev. Lett. 79 (26), 5254–5257.CrossRefGoogle Scholar
Langer, S. A., Goldstein, R. E. & Jackson, D. P. 1992 Dynamics of labyrinthine pattern formation in magnetic fluids. Phys. Rev. A 46 (8), 4894–4904.Google Scholar
Paterson, L. 1985 Fingering with miscible fluids in a Hele-Shaw cell. Phys. Fluids 28 (1), 26–30.Google Scholar
Rosensweig, R. E. 1997 Ferrohydrodynamics. Dover.Google Scholar
Wen, C. Y., Chen, C. Y. & Kuan, D. C. 2007a Experimental studies of labyrinthine instabilities of miscible ferrofluids in a Hele-Shaw cell. Phys. Fluids 19 (8), 084101.CrossRefGoogle Scholar
Wen, C. Y., Chen, C. Y., Kuan, D. C. & Wu, S. Y. 2007b Labyrinthine instability of a miscible magnetic drop. J. Magn. Magn. Mater. 310 (2), e1017–e1019.Google Scholar
Wen, C. Y., Chen, C. Y., Tsai, C. H. & Kuan, D. C. 2005 Labyrinthine instabilities of a magnetic droplet in a Hele-Shaw cell. Magnetohydrodynamics 41, 215–222.Google Scholar
Wen, C. Y., Lin, J. Z., Chen, M. Y., Chen, L. Q. & Liang, T. K. 2011 Effects of sweep rates of external magnetic fields on the labyrinthine instabilities of miscible magnetic fluids. J. Magn. Magn. Mater. 323 (10), 1258–1262.CrossRefGoogle Scholar
Wen, C. Y. & Su, W. P. 2005 Natural convection of magnetic fluid in a rectangular Hele-Shaw cell. J. Magn. Magn. Mater. 289, 299–302.Google Scholar
Wen, C. Y., Yeh, C. P., Tsai, C. H. & Fu, L. M. 2009 Rapid magnetic microfluidic mixer utilizing ac electromagnetic field. Electrophoresis 30 (24), 4179–4186.CrossRefGoogle ScholarPubMed

Li et al. supplementary movie

Experimental conditions: SR=5.6 Oe/s, H=100 Oe, EMG905 and h=1 mm

Download Li et al. supplementary movie(Video)
Video 860.2 KB