Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Alsina, José M.
Jongedijk, Cleo E.
and
van Sebille, Erik
2020.
Laboratory Measurements of the Wave‐Induced Motion of Plastic Particles: Influence of Wave Period, Plastic Size and Plastic Density.
Journal of Geophysical Research: Oceans,
Vol. 125,
Issue. 12,
Lenain, Luc
and
Pizzo, Nick
2020.
The Contribution of High-Frequency Wind-Generated Surface Waves to the Stokes Drift.
Journal of Physical Oceanography,
Vol. 50,
Issue. 12,
p.
3455.
Pizzo, Nick
Murray, Ethan
Smith, David Llewellyn
and
Lenain, Luc
2021.
The role of bandwidth in setting the breaking slope threshold of deep-water focusing wave packets.
Physics of Fluids,
Vol. 33,
Issue. 11,
Khait, Anatoliy
and
Ma, Zhihua
2021.
On an eddy viscosity model for energetic deep-water surface gravity wave breaking.
Journal of Fluid Mechanics,
Vol. 929,
Issue. ,
Grue, John
and
Osyka, Bodgan
2021.
Runup on a vertical column in strong water wave events.
Coastal Engineering,
Vol. 163,
Issue. ,
p.
103775.
Sinnis, James T.
Grare, Laurent
Lenain, Luc
and
Pizzo, Nick
2021.
Laboratory studies of the role of bandwidth in surface transport and energy dissipation of deep-water breaking waves.
Journal of Fluid Mechanics,
Vol. 927,
Issue. ,
Ruth, Daniel J.
Néel, Baptiste
Erinin, Martin A.
Mazzatenta, Megan
Jaquette, Robert
Veron, Fabrice
and
Deike, Luc
2022.
Three‐Dimensional Measurements of Air Entrainment and Enhanced Bubble Transport During Wave Breaking.
Geophysical Research Letters,
Vol. 49,
Issue. 16,
Kurniawan, Adi
Taylor, Paul H.
Orszaghova, Jana
Wolgamot, Hugh
and
Hansen, Jeff
2022.
Measuring a Rogue? An Investigation into an Apparent Giant Wave.
Journal of Atmospheric and Oceanic Technology,
Vol. 39,
Issue. 8,
p.
1129.
Larsen, Bjarke Eltard
Al-Obaidi, Mustafa Ali Abdullah
Guler, Hasan Gokhan
Carstensen, Stefan
Goral, Koray Deniz
Christensen, Erik Damgaard
Kerpen, Nils B.
Schlurmann, Torsten
and
Fuhrman, David R.
2023.
Experimental investigation on the nearshore transport of buoyant microplastic particles.
Marine Pollution Bulletin,
Vol. 187,
Issue. ,
p.
114610.
Kirezci, Cagil
Skvortsov, Alexei T.
Sgarioto, Daniel
and
Babanin, Alexander V.
2023.
Dispersion of tracer particles by wave turbulence.
Physica D: Nonlinear Phenomena,
Vol. 448,
Issue. ,
p.
133725.
Eeltink, D.
Calvert, R.
Swagemakers, J.E.
Xiao, Qian
and
van den Bremer, T.S.
2023.
Stochastic particle transport by deep-water irregular breaking waves.
Journal of Fluid Mechanics,
Vol. 971,
Issue. ,
McAllister, M.L.
Pizzo, N.
Draycott, S.
and
van den Bremer, T.S.
2023.
The influence of spectral bandwidth and shape on deep-water wave breaking onset.
Journal of Fluid Mechanics,
Vol. 974,
Issue. ,
Sanness Salmon, Henri R.
Baker, Lucia J.
Kozarek, Jessica L.
and
Coletti, Filippo
2023.
Effect of Shape and Size on the Transport of Floating Particles on the Free Surface in a Natural Stream.
Water Resources Research,
Vol. 59,
Issue. 10,
Ji, Chaoqun
Zhang, Jinfeng
Liu, Guangwei
Zhang, Qinghe
and
Shen, Xiaoteng
2024.
A settling velocity formula for irregular shaped microplastic fragments based on new shape factor: Influence of secondary motions.
Science of The Total Environment,
Vol. 955,
Issue. ,
p.
176857.
Hao, Xuanting
2024.
Quantifying Bioluminescent Light Intensity in Breaking Waves Using Numerical Simulations.
Geophysical Research Letters,
Vol. 51,
Issue. 20,
Feddersen, F.
Amador, Andre
Pick, Kanoa
Vizuet, A.
Quinn, Kaden
Wolfinger, Eric
MacMahan, J. H.
and
Fincham, Adam
2024.
The wavedrifter: a low-cost IMU-based Lagrangian drifter to observe steepening and overturning of surface gravity waves and the transition to turbulence.
Coastal Engineering Journal,
Vol. 66,
Issue. 1,
p.
44.
Callaghan, A. H.
Deane, G. B.
and
Stokes, M. Dale
2024.
A Comparison of Laboratory and Field Measurements of Whitecap Foam Evolution From Breaking Waves.
Journal of Geophysical Research: Oceans,
Vol. 129,
Issue. 1,
Calvert, R.
Peytavin, A.
Pham, Y.
Duhamel, A.
van der Zanden, J.
van Essen, S. M.
Sainte‐Rose, B.
and
van den Bremer, T. S.
2024.
A Laboratory Study of the Effects of Size, Density, and Shape on the Wave‐Induced Transport of Floating Marine Litter.
Journal of Geophysical Research: Oceans,
Vol. 129,
Issue. 7,
Xiao, Q.
McAllister, M.L.
Adcock, T.A.A.
and
van den Bremer, T.S.
2025.
Laboratory study of the enhanced wave-induced drift of large rectangular floating objects.
Journal of Fluid Mechanics,
Vol. 1008,
Issue. ,
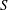 $S$, the linear prediction of the maximum slope at focusing, while the surface transport due to non-breaking waves scales with
$S$, the linear prediction of the maximum slope at focusing, while the surface transport due to non-breaking waves scales with 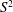 $S^{2}$, in agreement with the classical Stokes prediction.
$S^{2}$, in agreement with the classical Stokes prediction.