Hostname: page-component-586b7cd67f-t8hqh Total loading time: 0 Render date: 2024-11-26T06:16:44.907Z Has data issue: false hasContentIssue false
  • English
  • Français

Koopman mode expansions between simple invariant solutions

Published online by Cambridge University Press:  19 September 2019

Jacob Page Open the ORCID record for Jacob Page [Opens in a new window]  and
Rich R. Kerswell
Jacob Page*
Affiliation:
DAMTP, Centre for Mathematical Sciences, University of Cambridge, CambridgeCB3 0WA, UK
Rich R. Kerswell*
Affiliation:
DAMTP, Centre for Mathematical Sciences, University of Cambridge, CambridgeCB3 0WA, UK
*
†Email addresses for correspondence: [email protected], [email protected]
†Email addresses for correspondence: [email protected], [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

A Koopman decomposition is a powerful method of analysis for fluid flows leading to an apparently linear description of nonlinear dynamics in which the flow is expressed as a superposition of fixed spatial structures with exponential time dependence. Attempting a Koopman decomposition is simple in practice due to a connection with dynamic mode decomposition (DMD). However, there are non-trivial requirements for the Koopman decomposition and DMD to overlap, which mean it is often difficult to establish whether the latter is truly approximating the former. Here, we focus on nonlinear systems containing multiple simple invariant solutions where it is unclear how to construct a consistent Koopman decomposition, or how DMD might be applied to locate these solutions. First, we derive a Koopman decomposition for a heteroclinic connection in a Stuart–Landau equation revealing two possible expansions. The expansions are centred about the two fixed points of the equation and extend beyond their linear subspaces before breaking down at a cross-over point in state space. Well-designed DMD can extract the two expansions provided that the time window does not contain this cross-over point. 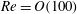We then apply DMD to the Navier–Stokes equations near to a heteroclinic connection in low Reynolds number ($Re=O(100)$) plane Couette flow where there are multiple simple invariant solutions beyond the constant shear basic state. This reveals as many different Koopman decompositions as simple invariant solutions present and once more indicates the existence of cross-over points between the expansions in state space. Again, DMD can extract these expansions only if it does not include a cross-over point. Our results suggest that in a dynamical system possessing multiple simple invariant solutions, there are generically places in phase space – plausibly hypersurfaces delineating the boundary of a local Koopman expansion – across which the dynamics cannot be represented by a convergent Koopman expansion.

JFM classification

Nonlinear Dynamical Systems: Low-dimensional models Instability: Transition to turbulence
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 879 , 25 November 2019 , pp. 1 - 27
Check for updates
Copyright
© 2019 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Ahmed, M. A. & Sharma, A. S.2017 New equilibrium solution branches of plane Couette flow discovered using a project-then-search method. Preprint, arXiv:1706.05312.Google Scholar
Arbabi, H. & Mezić, I. 2017 Study of dynamics in post-transient flows using Koopman mode decomposition. Phys. Rev. Fluids 2, 124402.10.1103/PhysRevFluids.2.124402Google Scholar
Avila, M., Mellibovsky, F., Roland, N. & Hof, B. 2013 Streamwise-localized solutions at the onset of turbulence in pipe flow. Phys. Rev. Lett. 110, 224502.10.1103/PhysRevLett.110.224502Google Scholar
Bagheri, S. 2013 Koopman-mode decomposition of the cylinder wake. J. Fluid Mech. 726, 596–623.10.1017/jfm.2013.249Google Scholar
Brand, E. & Gibson, J. F. 2014 A doubly localized equilibrium solution of plane Couette flow. J. Fluid Mech. 750, R3.10.1017/jfm.2014.285Google Scholar
Brunton, B. W., Johnson, L. A., Ojemann, J. G. & Kutz, J. N. 2016a Extracting spatialtemporal coherent patterns in large-scale neural recordings using dynamic mode decomposition. J. Neurosci. Meth. 258, 1–15.10.1016/j.jneumeth.2015.10.010Google Scholar
Brunton, S. L., Brunton, B. W., Proctor, J. L. & Kutz, J. N. 2016b Koopman invariant subspaces and finite linear repesentations of nonlinear dynamical systems for control. PLoS ONE 11 (2), e0150171.10.1371/journal.pone.0150171Google Scholar
Carleman, T. 1932 Application de la theories des equations integrales lineaires aux systemes dequations differentielles non lineaires. Acta. Math. 59, 63–87.10.1007/BF02546499Google Scholar
Chandler, G. J. & Kerswell, R. R. 2013 Invariant recurrent solutions embedded in a turbulent two-dimensional kolmogorov flow. J. Fluid Mech. 722, 554–595.10.1017/jfm.2013.122Google Scholar
Chantry, M., Willis, A. P. & Kerswell, R. R. 2014 Genesis of streamwise-localised solutions from globally periodic traveling waves in pipe flow. Phys. Rev. Lett. 112, 164501.10.1103/PhysRevLett.112.164501Google Scholar
Cvitanovic, P. & Gibson, J. F. 2010 Geometry of the turbulence in wall-bounded shear flows: periodic orbits. Phys. Scr. T 142, 014007.Google Scholar
Deguchi, K. 2017 Scaling of small vortices in stably stratified shear flows. J. Fluid Mech. 821, 582–594.10.1017/jfm.2017.213Google Scholar
Eaves, T. S., Caulfield, C. P. & Mezic, I. 2016 Transition to turbulence: highway through the edge of chaos is charted by Koopman modes. APS Bull.; http://meetings.aps.org/link/BAPS.2016.DFD.D8.3.Google Scholar
Eckhardt, B., Schneider, T. M., Hof, B. & Westerweel, J. 2007 Turbulence transition in pipe flow. Annu. Rev. Fluid Mech. 39, 447–468.10.1146/annurev.fluid.39.050905.110308Google Scholar
Faisst, H. & Eckhardt, B. 2003 Traveling waves in pipe flow. Phys. Rev. Lett. 91, 224502.10.1103/PhysRevLett.91.224502Google Scholar
Gaspard, P. 1998 Chaos, Scattering and Statistical Mechanics, 1st edn. Cambridge University Press.10.1017/CBO9780511628856Google Scholar
Gaspard, P., Nicolis, G., Provata, A. & Tasaki, S. 1995 Spectral signature of the pitchfork bifurcation: Liouville equation approach. Phys. Rev. E 51, 74.Google Scholar
Gibson, J. F. & Brand, E. 2014 Spanwise-localized solutions of planar shear flows. J. Fluid Mech. 745, 25–61.10.1017/jfm.2014.89Google Scholar
Gibson, J. F., Halcrow, J. & Cvitanovic, P. 2008 Visualizing the geometry of state space in plane Couette flow. J. Fluid Mech. 611, 107–130.10.1017/S002211200800267XGoogle Scholar
Gibson, J. F., Halcrow, J. & Cvitanovic, P. 2009 Equilibrium and travelling-wave solutions of plane Couette flow. J. Fluid Mech. 638, 243–266.10.1017/S0022112009990863Google Scholar
Hall, P. & Sherwin, S. 2010 Streamwise vortices in shear flows: harbingers of transition and the skeleton of coherent structures. J. Fluid Mech. 661, 178–205.10.1017/S0022112010002892Google Scholar
Hamilton, J. M., Kim, J. & Waleffe, F. 1995 Regeneration mechanisms of near-wall turbulence structures. J. Fluid Mech. 287, 317–348.10.1017/S0022112095000978Google Scholar
Jovanović, M. R., Schmid, P. J. & Nichols, J. W. 2014 Sparsity-promoting dynamic mode decomposition. Phys. Fluids 26, 024103.10.1063/1.4863670Google Scholar
Kawahara, G. & Kida, S. 2001 Periodic motion embedded in plane Couette turbulence: regeneration cycle and burst. J. Fluid Mech. 449, 291–300.10.1017/S0022112001006243Google Scholar
Kawahara, G., Uhlmann, M. & van Veen, L. 2012 The significance of simple invariant solutions in turbulent flows. Annu. Rev. Fluid Mech. 44 (1), 203–225.10.1146/annurev-fluid-120710-101228Google Scholar
Kerswell, R. R. 2005 Recent progress in understanding the transition to turbulence in a pipe. Nonlinearity 18, R17–R44.10.1088/0951-7715/18/6/R01Google Scholar
Koopman, B. O. 1931 Hamiltonian systems and transformations in Hilbert space. Proc. Natl Acad. Sci. 17 (5), 315–318.10.1073/pnas.17.5.315Google Scholar
Kutz, J. N., Brunton, S. L., Brunton, B. W. & Proctor, J. L. 2016a Dynamic Mode Decomposition: Data-Driven Modeling of Complex Systems, 1st edn. SIAM.10.1137/1.9781611974508Google Scholar
Kutz, J. N., Fu, X. & Brunton, S. L. 2016b Multiresolution dynamic mode decomposition. SIAM J. Appl. Dyn. Syst. 15, 713–735.10.1137/15M1023543Google Scholar
Lucas, D., Caulfield, C. P. & Kerswell, R. R. 2017 Layer formation in horizontally forced stratified turbulence: connecting exact coherent structures to linear instabilities. J. Fluid Mech. 832, 409–437.10.1017/jfm.2017.661Google Scholar
Lusch, B., Kutz, J. N. & Brunton, S. L. 2018 Deep learning for universal linear embeddings of nonlinear dynamics. Nat. Commun. 9 (1), 4950.10.1038/s41467-018-07210-0Google Scholar
Mezić, I. 2005 Spectral properties of dynamical systems, model reduction and decompositions. Nonlinear Dyn. 41, 309–325.10.1007/s11071-005-2824-xGoogle Scholar
Mezić, I. 2013 Analysis of fluid flows via spectral properties of the Koopman operator. Annu. Rev. Fluid Mech. 45, 357–378.10.1146/annurev-fluid-011212-140652Google Scholar
Mezic, I.2017 Koopman operator spectrum and data analysis. Preprint, arXiv:1702.07597.Google Scholar
Mezic, I. & Banaszuk, A. 2004 Comparison of systems with complex behavior. Physica D 197, 101–133.Google Scholar
Nagata, M. 1990 Three-dimensional finite-amplitude solutions in plane Couette flow: bifurcation from infinity. J. Fluid Mech. 217, 519–527.10.1017/S0022112090000829Google Scholar
Olvera, D. & Kerswell, R. R. 2017 Exact coherent structures in stably stratified plane Couette flow. J. Fluid Mech. 826, 583–614.10.1017/jfm.2017.447Google Scholar
Page, J. & Kerswell, R. R. 2018 Koopman analysis of Burgers equation. Phys. Rev. Fluids 3, 071901(R).10.1103/PhysRevFluids.3.071901Google Scholar
Rowley, C. W. & Dawson, S. T. M. 2017 Model reduction for flow analysis and control. Annu. Rev. Fluid Mech. 49, 387–417.10.1146/annurev-fluid-010816-060042Google Scholar
Rowley, C. W., Mezić, I., Bagheri, S., Schlatter, P. & Henningson, D. S. 2009 Spectral analysis of nonlinear flows. J. Fluid Mech. 641, 115–127.10.1017/S0022112009992059Google Scholar
Schmid, P. J. 2010 Dynamic mode decomposition of numerical and experimental data. J. Fluid Mech. 656, 5–28.10.1017/S0022112010001217Google Scholar
Schneider, T. M., Eckhardt, B. & Yorke, J. A. 2007 Turbulence transition and the edge of chaos in pipe flow. Phys. Rev. Lett. 99, 034502.10.1103/PhysRevLett.99.034502Google Scholar
Schneider, T. M., Gibson, J. F. & Burke, J. 2010 Snakes and ladders: localized solutions of plane Couette flow. Phys. Rev. Lett. 104, 104501.10.1103/PhysRevLett.104.104501Google Scholar
Sharma, A. S., Mezić, I. & McKeon, B. J. 2016 Correspondence between Koopman mode decompositions, resolvent mode decomposition and invariant solutions of the Navier–Stokes equations. Phys. Rev. Fluids 1, 032402(R).10.1103/PhysRevFluids.1.032402Google Scholar
Tu, J. H., Rowley, C. W., Luchtenburg, D. M., Brunton, S. L. & Kutz, J. N. 2014 On dynamic mode decomposition: theory and applications. J. Comput. Dyn. 1 (2), 391–421.10.3934/jcd.2014.1.391Google Scholar
Uhlmann, M., Kawahara, G. & Pinelli, A. 2010 Traveling-waves consistent with turbulence-driven secondary flow in a square duct. Phys. Fluids 22 (8), 084102.10.1063/1.3466661Google Scholar
Viswanath, D. 2007 Recurrent motions within plane Couette turbulence. J. Fluid Mech. 580, 339–358.10.1017/S0022112007005459Google Scholar
Waleffe, F. 1997 On a self-sustaining process in shear flows. Phys. Fluids 9, 883–900.10.1063/1.869185Google Scholar
Waleffe, F. 2001 Exact coherent structures in channel flow. J. Fluid Mech. 435, 93–102.10.1017/S0022112001004189Google Scholar
Wang, J., Gibson, J. & Waleffe, F. 2007 Lower branch coherent states in shear flows: transition and control. Phys. Rev. Lett. 98, 204501.10.1103/PhysRevLett.98.204501Google Scholar
Wedin, H. & Kerswell, R. R. 2004 Exact coherent structures in pipe flow: travelling wave solutions. J. Fluid Mech. 508, 333–371.10.1017/S0022112004009346Google Scholar
Williams, M. O., Kevrekidis, I. G. & Rowley, C. W. 2015 A data-driven approximation of the Koopman operator: extending dynamic mode decomposition. J. Nonlinear Sci. 25 (6), 1307–1346.10.1007/s00332-015-9258-5Google Scholar
Zammert, S. & Eckhardt, B. 2014 Streamwise and doubly-localized periodic orbits in plane Poiseuille flow. J. Fluid Mech. 761, 348–359.10.1017/jfm.2014.633Google Scholar