Hostname: page-component-669899f699-ggqkh Total loading time: 0 Render date: 2025-05-04T08:06:56.266Z Has data issue: false hasContentIssue false
  • English
  • Français

Keplerian turbulence in Taylor–Couette flow of dilute polymeric solutions

Published online by Cambridge University Press:  27 November 2024

Fenghui Lin Open the ORCID record for Fenghui Lin [Opens in a new window] ,
Jiaxing Song Open the ORCID record for Jiaxing Song [Opens in a new window] ,
Nansheng Liu Open the ORCID record for Nansheng Liu [Opens in a new window] ,
Luoqin Liu Open the ORCID record for Luoqin Liu [Opens in a new window] ,
Xi-Yun Lu Open the ORCID record for Xi-Yun Lu [Opens in a new window]  and
Bamin Khomami Open the ORCID record for Bamin Khomami [Opens in a new window]
Fenghui Lin
Affiliation:
Department of Modern Mechanics, University of Science and Technology of China, Hefei, Anhui 230026, PR China
Jiaxing Song
Affiliation:
Department of Modern Mechanics, University of Science and Technology of China, Hefei, Anhui 230026, PR China
Nansheng Liu*
Affiliation:
Department of Modern Mechanics, University of Science and Technology of China, Hefei, Anhui 230026, PR China
Luoqin Liu
Affiliation:
Department of Modern Mechanics, University of Science and Technology of China, Hefei, Anhui 230026, PR China
Xi-Yun Lu
Affiliation:
Department of Modern Mechanics, University of Science and Technology of China, Hefei, Anhui 230026, PR China
Bamin Khomami
Affiliation:
Department of Chemical and Biomolecular Engineering, University of Tennessee, Knoxville, TN 37996, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

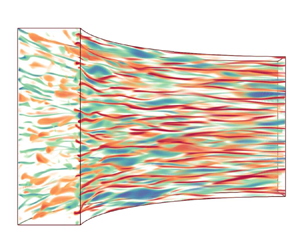
Turbulent flow induced by elastorotational instability in viscoelastic Taylor–Couette flow (TCF) with Keplerian rotation is analogous to a turbulent accretion disk destabilized by magnetorotational instability. We examine this novel viscoelastic Keplerian turbulence via direct numerical simulations (DNS) for the shear Reynolds number ($Re$) ranging from $10^2$ to $10^4$. The observed characteristic flow structure consists of penetrating streamwise vortices with axial length scales much smaller than the gap width, distinct from the classic centrifugally induced Taylor vortices, which have axial lengths of the gap width. These intriguing vortices persist for the wide $Re$ range considered and give rise to intriguing scaling behaviour in key flow quantities. Specifically, the characteristic axial length of the penetrating vortices is shown to scale as $Re^{-0.22}$; the angular momentum transport scales as $Re^{0.42}$; the kinetic and elastic boundary-layer thicknesses based on angular velocity and hoop stress near the inner cylinder wall scale as $Re^{-0.48}$ and $Re^{-0.49}$, respectively. This implies that the viscoelastic Keplerian turbulence belongs to the classical turbulent regime of TCF with the Prandtl–Blasius-type boundary layer. Furthermore, we present an analytical relation between the viscous and elastic dissipation rates of kinetic energy and the angular momentum transport and in turn demonstrate its validity using our DNS data. This study has paved the way for future research to explore astrophysics-related Keplerian turbulence and angular momentum transport via the scaling relations of the analogous TCF of dilute polymeric solutions.

JFM classification

Non-Newtonian Flows: Viscoelasticity Turbulent Flows: Rotating turbulence
Type
JFM Rapids
Information
Journal of Fluid Mechanics , Volume 1000 , 10 December 2024 , R3
Check for updates
Copyright
© The Author(s), 2024. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

Footnotes

‡

Present address: Max Planck Institute for Dynamics and Self-Organization, Göttingen 37077, Germany

References

Avila, M. 2012 Stability and angular-momentum transport of fluid flows between corotating cylinders. Phys. Rev. Lett. 108, 124501.CrossRefGoogle ScholarPubMed
Bai, Y., Crumeyrolle, O. & Mutabazi, I. 2015 Viscoelastic Taylor–Couette instability as analog of the magnetorotational instability. Phys. Rev. E 92, 031001.CrossRefGoogle ScholarPubMed
Bai, Y., Vieu, T., Crumeyrolle, O. & Mutabazi, I. 2021 Viscoelastic Taylor–Couette instability in the Keplerian regime. Geophys. Astrophys. Fluid Dyn. 115, 322–344.CrossRefGoogle Scholar
Boldyrev, S., Huynh, D. & Pariev, V. 2009 Analog of astrophysical magnetorotational instability in a Couette–Taylor flow of polymer fluids. Phys. Rev. E 80, 066310.CrossRefGoogle Scholar
Brauckmann, H.J. & Eckhardt, B. 2017 Marginally stable and turbulent boundary layers in low-curvature Taylor–Couette flow. J. Fluid Mech. 815, 149–168.CrossRefGoogle Scholar
Dey, S., Chatterjee, P., Murthy, O.V.S.N., Korsós, M.B., Liu, J., Nelson, C.J. & Erdélyi, R. 2022 Polymeric jets throw light on the origin and nature of the forest of solar spicules. Nat. Phys. 18, 595–600.CrossRefGoogle Scholar
Dong, S. 2008 Turbulent flow between counter-rotating concentric cylinders: a direct numerical simulation study. J. Fluid Mech. 615, 371–399.CrossRefGoogle Scholar
Eckhardt, B., Grossmann, S. & Lohse, D. 2007 Torque scaling in turbulent Taylor–Couette flow between independently rotating cylinders. J. Fluid Mech. 581, 221–250.CrossRefGoogle Scholar
Grossmann, S., Lohse, D. & Sun, C. 2016 High–Reynolds number Taylor–Couette turbulence. Annu. Rev. Fluid Mech. 48, 53–80.CrossRefGoogle Scholar
Ji, H., Burin, M., Schartman, E. & Goodman, J. 2006 Hydrodynamic turbulence cannot transport angular momentum effectively in astrophysical disks. Nature 444, 343–346.CrossRefGoogle ScholarPubMed
Ji, H. & Goodman, J. 2023 Taylor–Couette flow for astrophysical purposes. Phil. Trans. R. Soc. A 381, 20220119.CrossRefGoogle ScholarPubMed
Landau, L.D. & Lifshitz, E.M. 1987 Fluid Mechanics, 2nd edn. Course of Theoretical Physics, vol. 6. Butterworth Heinemann.Google Scholar
Larson, R.G. & Desai, P.S. 2015 Modeling the rheology of polymer melts and solutions. Annu. Rev. Fluid Mech. 47, 47–65.CrossRefGoogle Scholar
Larson, R.G., Shaqfeh, E.S.G. & Muller, S.J. 1990 A purely elastic instability in Taylor–Couette flow. J. Fluid Mech. 218, 573–600.CrossRefGoogle Scholar
Lin, F., Wan, Z., Zhu, Y., Liu, N., Lu, X. & Khomami, B. 2022 High-fidelity robust and efficient finite difference algorithm for simulation of polymer-induced turbulence in cylindrical coordinates. J. Non-Newtonian Fluid Mech. 307, 104875.CrossRefGoogle Scholar
Lopez, J.M. & Avila, M. 2017 Boundary-layer turbulence in experiments on quasi-Keplerian flows. J. Fluid Mech. 817, 21–34.CrossRefGoogle Scholar
Mishra, A., Mamatsashvili, G. & Stefani, F. 2023 Nonlinear evolution of magnetorotational instability in a magnetized Taylor–Couette flow: scaling properties and relation to upcoming DRESDYN-MRI experiment. Phys. Rev. Fluids 8, 083902.CrossRefGoogle Scholar
Ogilvie, G.I. & Potter, A.T. 2008 Magnetorotational-type instability in Couette–Taylor flow of a viscoelastic polymer liquid. Phys. Rev. Lett. 100, 074503.CrossRefGoogle ScholarPubMed
Ogilvie, G.I. & Proctor, M.R.E. 2003 On the relation between viscoelastic and magnetohydrodynamic flows and their instabilities. J. Fluid Mech. 476, 389–409.CrossRefGoogle Scholar
Ostilla-Mónico, R., Stevens, R.J.A.M., Grossmann, S., Verzicco, R. & Lohse, D. 2013 Optimal Taylor–Couette flow: direct numerical simulations. J. Fluid Mech. 719, 14–46.CrossRefGoogle Scholar
Ostilla-Mónico, R., Verzicco, R., Grossmann, S. & Lohse, D. 2014 Turbulence decay towards the linearly stable regime of Taylor–Couette flow. J. Fluid Mech. 748, R3.CrossRefGoogle Scholar
Schartman, E., Ji, H., Burin, M.J. & Goodman, J. 2012 Stability of quasi-Keplerian shear flow in a laboratory experiment. Astron. Astrophys. 543, A94.CrossRefGoogle Scholar
Shi, L., Hof, B., Rampp, M. & Avila, M. 2017 Hydrodynamic turbulence in quasi-Keplerian rotating flows. Phys. Fluids 29, 044107.CrossRefGoogle Scholar
Somasi, M. & Khomami, B. 2000 Linear stability and dynamics of viscoelastic flows using time-dependent stochastic simulation techniques. J. Non-Newtonian Fluid Mech. 93, 339–362.CrossRefGoogle Scholar
Song, J., Lin, F., Liu, N., Lu, X. & Khomami, B. 2021 Direct numerical simulation of inertio-elastic turbulent Taylor–Couette flow. J. Fluid Mech. 926, A37.CrossRefGoogle Scholar
Song, J., Teng, H., Liu, N., Ding, H., Lu, X. & Khomami, B. 2019 The correspondence between drag enhancement and vortical structures in turbulent Taylor–Couette flows with polymer additives: a study of curvature dependence. J. Fluid Mech. 881, 602–616.CrossRefGoogle Scholar
Thomas, D.G., Khomami, B. & Sureshkumar, R. 2009 Nonlinear dynamics of viscoelastic Taylor–Couette flow: effect of elasticity on pattern selection, molecular conformation and drag. J. Fluid Mech. 620, 353–382.CrossRefGoogle Scholar
Vieu, T. & Mutabazi, I. 2019 A theory of magnetic-like fields for viscoelastic fluids. J. Fluid Mech. 865, 460–491.CrossRefGoogle Scholar