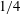 $1/4$
$1/4$Published online by Cambridge University Press: 23 September 2019
We study the dynamical system of a two-dimensional, forced, stratified mixing layer at finite Reynolds number 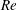 $Re$, and Prandtl number
$Re$, and Prandtl number 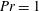 $Pr=1$. We consider a hyperbolic tangent background velocity profile in the two cases of hyperbolic tangent and uniform background buoyancy stratifications, in a domain of fixed, finite width and height. The system is forced in such a way that these background profiles are a steady solution of the governing equations. As is well known, if the minimum gradient Richardson number of the flow,
$Pr=1$. We consider a hyperbolic tangent background velocity profile in the two cases of hyperbolic tangent and uniform background buoyancy stratifications, in a domain of fixed, finite width and height. The system is forced in such a way that these background profiles are a steady solution of the governing equations. As is well known, if the minimum gradient Richardson number of the flow, 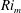 $Ri_{m}$, is less than a certain critical value
$Ri_{m}$, is less than a certain critical value 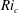 $Ri_{c}$, the flow is linearly unstable to Kelvin–Helmholtz instability in both cases. Using Newton–Krylov iteration, we find steady, two-dimensional, finite-amplitude elliptical vortex structures – i.e. ‘Kelvin–Helmholtz billows’ – existing above
$Ri_{c}$, the flow is linearly unstable to Kelvin–Helmholtz instability in both cases. Using Newton–Krylov iteration, we find steady, two-dimensional, finite-amplitude elliptical vortex structures – i.e. ‘Kelvin–Helmholtz billows’ – existing above 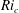 $Ri_{c}$. Bifurcation diagrams are produced using branch continuation, and we explore how these diagrams change with varying
$Ri_{c}$. Bifurcation diagrams are produced using branch continuation, and we explore how these diagrams change with varying 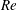 $Re$. In particular, when
$Re$. In particular, when 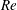 $Re$ is sufficiently high we find that finite-amplitude Kelvin–Helmholtz billows exist when
$Re$ is sufficiently high we find that finite-amplitude Kelvin–Helmholtz billows exist when 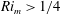 $Ri_{m}>1/4$ for the background flow, which is linearly stable by the Miles–Howard theorem. For the uniform background stratification, we give a simple explanation of the dynamical system, showing the dynamics can be understood on a two-dimensional manifold embedded in state space, and demonstrate the cases in which the system is bistable. In the case of a hyperbolic tangent stratification, we also describe a new, slow-growing, linear instability of the background profiles at finite
$Ri_{m}>1/4$ for the background flow, which is linearly stable by the Miles–Howard theorem. For the uniform background stratification, we give a simple explanation of the dynamical system, showing the dynamics can be understood on a two-dimensional manifold embedded in state space, and demonstrate the cases in which the system is bistable. In the case of a hyperbolic tangent stratification, we also describe a new, slow-growing, linear instability of the background profiles at finite 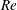 $Re$, which complicates the dynamics.
$Re$, which complicates the dynamics.