Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Ellingsen, Simen Å.
2014.
Initial surface disturbance on a shear current: The Cauchy-Poisson problem with a twist.
Physics of Fluids,
Vol. 26,
Issue. 8,
Moisy, Frédéric
and
Rabaud, Marc
2014.
Mach-like capillary-gravity wakes.
Physical Review E,
Vol. 90,
Issue. 2,
Wang, Ben-long
Guo, Xiao-yu
Liu, Hua
and
He, Chen
2014.
Numerical simulations of wake signatures around high-speed ships.
Journal of Hydrodynamics,
Vol. 26,
Issue. 6,
p.
986.
Pethiyagoda, Ravindra
McCue, Scott W.
Moroney, Timothy J.
and
Back, Julian M.
2014.
Jacobian-free Newton–Krylov methods with GPU acceleration for computing nonlinear ship wave patterns.
Journal of Computational Physics,
Vol. 269,
Issue. ,
p.
297.
Rabaud, Marc
and
Moisy, Frédéric
2014.
Du neuf dans les sillages.
Reflets de la physique,
p.
10.
Ellingsen, Simen Å.
2014.
Ship waves in the presence of uniform vorticity.
Journal of Fluid Mechanics,
Vol. 742,
Issue. ,
Dias, F.
2014.
Ship waves and Kelvin.
Journal of Fluid Mechanics,
Vol. 746,
Issue. ,
p.
1.
Moisy, F.
and
Rabaud, M.
2014.
Scaling of far-field wake angle of nonaxisymmetric pressure disturbance.
Physical Review E,
Vol. 89,
Issue. 6,
Benzaquen, Michael
Darmon, Alexandre
and
Raphaël, Elie
2014.
Wake pattern and wave resistance for anisotropic moving disturbances.
Physics of Fluids,
Vol. 26,
Issue. 9,
Gomit, Guillaume
Rousseaux, Germain
Chatellier, Ludovic
Calluaud, Damien
and
David, Laurent
2014.
Spectral analysis of ship waves in deep water from accurate measurements of the free surface elevation by optical methods.
Physics of Fluids,
Vol. 26,
Issue. 12,
Noblesse, Francis
He, Jiayi
Zhu, Yi
Hong, Liang
Zhang, Chenliang
Zhu, Renchuan
and
Yang, Chi
2014.
Why can ship wakes appear narrower than Kelvin’s angle?.
European Journal of Mechanics - B/Fluids,
Vol. 46,
Issue. ,
p.
164.
Pethiyagoda, Ravindra
McCue, Scott W.
and
Moroney, Timothy J.
2014.
What is the apparent angle of a Kelvin ship wave pattern?.
Journal of Fluid Mechanics,
Vol. 758,
Issue. ,
p.
468.
Torsvik, T.
Soomere, T.
Didenkulova, I.
and
Sheremet, A.
2015.
Identification of ship wake structures by a time–frequency method.
Journal of Fluid Mechanics,
Vol. 765,
Issue. ,
p.
229.
Miao, Sha
and
Liu, Yuming
2015.
Wave pattern in the wake of an arbitrary moving surface pressure disturbance.
Physics of Fluids,
Vol. 27,
Issue. 12,
Zhu, Yi
He, Jiayi
Zhang, Chenliang
Wu, Huiyu
Wan, Decheng
Zhu, Renchuan
and
Noblesse, Francis
2015.
Farfield waves created by a monohull ship in shallow water.
European Journal of Mechanics - B/Fluids,
Vol. 49,
Issue. ,
p.
226.
Parnell, Kevin E.
Soomere, Tarmo
Zaggia, Luca
Rodin, Artem
Lorenzetti, Giuliano
Rapaglia, John
and
Scarpa, Gian Marco
2015.
Ship-induced solitary Riemann waves of depression in Venice Lagoon.
Physics Letters A,
Vol. 379,
Issue. 6,
p.
555.
Shi, Xihang
Lin, Xiao
Gao, Fei
Xu, Hongyi
Yang, Zhaoju
and
Zhang, Baile
2015.
Caustic graphene plasmons with Kelvin angle.
Physical Review B,
Vol. 92,
Issue. 8,
Pethiyagoda, Ravindra
McCue, Scott W.
and
Moroney, Timothy J.
2015.
Wake angle for surface gravity waves on a finite depth fluid.
Physics of Fluids,
Vol. 27,
Issue. 6,
Zhang, Chenliang
He, Jiayi
Zhu, Yi
Yang, Chen-Jun
Li, Wei
Zhu, Yifei
Lin, Muyuan
and
Noblesse, Francis
2015.
Interference effects on the Kelvin wake of a monohull ship represented via a continuous distribution of sources.
European Journal of Mechanics - B/Fluids,
Vol. 51,
Issue. ,
p.
27.
Arzhannikov, A. V.
and
Kotelnikov, I. A.
2016.
Excitation of ship waves by a submerged object: New solution to the classical problem.
Physical Review E,
Vol. 94,
Issue. 2,
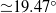 ${\simeq }19. 4{7}^{\circ } $. However a recent study by Rabaud and Moisy based on the observation of airborne images showed that the wake angle seems to decrease as the Froude number
${\simeq }19. 4{7}^{\circ } $. However a recent study by Rabaud and Moisy based on the observation of airborne images showed that the wake angle seems to decrease as the Froude number 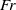 $Fr$ increases, scaling as
$Fr$ increases, scaling as 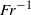 $F{r}^{- 1} $ for large Froude numbers. To explain such observations they make the strong hypothesis that an object of size
$F{r}^{- 1} $ for large Froude numbers. To explain such observations they make the strong hypothesis that an object of size 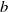 $b$ cannot generate wavelengths larger than
$b$ cannot generate wavelengths larger than 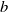 $b$. Without the need of such an assumption and modelling the moving object by an axisymmetric pressure field, we analytically show that the angle corresponding to the maximum amplitude of the waves scales as
$b$. Without the need of such an assumption and modelling the moving object by an axisymmetric pressure field, we analytically show that the angle corresponding to the maximum amplitude of the waves scales as 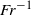 $F{r}^{- 1} $ for large Froude numbers, whereas the angle delimiting the wake region outside which the surface is essentially flat remains constant and equal to the Kelvin angle for all
$F{r}^{- 1} $ for large Froude numbers, whereas the angle delimiting the wake region outside which the surface is essentially flat remains constant and equal to the Kelvin angle for all 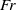 $Fr$.
$Fr$.