Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Prestridge, Kathy
2018.
Experimental adventures in variable-density mixing.
Physical Review Fluids,
Vol. 3,
Issue. 11,
Zhou, Ye
Clark, Timothy T.
Clark, Daniel S.
Gail Glendinning, S.
Aaron Skinner, M.
Huntington, Channing M.
Hurricane, Omar A.
Dimits, Andris M.
and
Remington, Bruce A.
2019.
Turbulent mixing and transition criteria of flows induced by hydrodynamic instabilities.
Physics of Plasmas,
Vol. 26,
Issue. 8,
Samie, Milad
Lavoie, Philippe
and
Pollard, Andrew
2020.
A scale-dependent coherence analysis of turbulent round jets including the effects of shear layer manipulation.
International Journal of Heat and Fluid Flow,
Vol. 82,
Issue. ,
p.
108524.
Aslangil, Denis
Livescu, Daniel
and
Banerjee, Arindam
2020.
Effects of Atwood and Reynolds numbers on the evolution of buoyancy-driven homogeneous variable-density turbulence.
Journal of Fluid Mechanics,
Vol. 895,
Issue. ,
Baltzer, Jon R.
and
Livescu, Daniel
2020.
Variable-density effects in incompressible non-buoyant shear-driven turbulent mixing layers.
Journal of Fluid Mechanics,
Vol. 900,
Issue. ,
Thiesset, F.
Duret, B.
Ménard, T.
Dumouchel, C.
Reveillon, J.
and
Demoulin, F. X.
2020.
Liquid transport in scale space.
Journal of Fluid Mechanics,
Vol. 886,
Issue. ,
Wattananusorn, S.
2020.
Non–decay of complex scalar field fluctuations in isotropic turbulence.
Chemical Engineering Science,
Vol. 218,
Issue. ,
p.
115463.
Troshin, Alexey
Bakhne, Sergey
and
Sabelnikov, Vladimir
2021.
Progress in Turbulence IX.
Vol. 267,
Issue. ,
p.
297.
Ivashchenko, V. A.
Palkin, E. V.
Ryzhenkov, V. O.
and
Mullyadzhanov, R. I.
2021.
POD-analysis of the near field of a turbulent circular jet when mixing gases of different densities.
Thermophysics and Aeromechanics,
Vol. 28,
Issue. 1,
p.
55.
Hellinger, Petr
Verdini, Andrea
Landi, Simone
Papini, Emanuele
Franci, Luca
and
Matteini, Lorenzo
2021.
Scale dependence and cross-scale transfer of kinetic energy in compressible hydrodynamic turbulence at moderate Reynolds numbers.
Physical Review Fluids,
Vol. 6,
Issue. 4,
Arun, S.
Sameen, A.
Srinivasan, Balaji
and
Girimaji, Sharath S.
2021.
Scale-space energy density function transport equation for compressible inhomogeneous turbulent flows.
Journal of Fluid Mechanics,
Vol. 920,
Issue. ,
Fratantonio, Dominique
Lai, Chris C. K.
Charonko, John
and
Prestridge, Kathy
2021.
Beyond Taylor’s hypothesis: a novel volumetric reconstruction of velocity and density fields for variable‑density and shear flows.
Experiments in Fluids,
Vol. 62,
Issue. 4,
Baj, P.
Alves Portela, F.
and
Carter, D.W.
2022.
On the simultaneous cascades of energy, helicity, and enstrophy in incompressible homogeneous turbulence.
Journal of Fluid Mechanics,
Vol. 952,
Issue. ,
Wu, Huijie
and
Wang, Binbin
2023.
Spectral turbulence kinetic energy budget and scale-based velocity decomposition for turbulence in bubble plumes.
Physics of Fluids,
Vol. 35,
Issue. 6,
Marino, Raffaele
and
Sorriso-Valvo, Luca
2023.
Scaling laws for the energy transfer in space plasma turbulence.
Physics Reports,
Vol. 1006,
Issue. ,
p.
1.
Noble, Christopher D.
Ames, Alex M.
McConnell, Raymond
Oakley, Jason
Rothamer, David A.
and
Bonazza, Riccardo
2023.
Simultaneous measurements of kinetic and scalar energy spectrum time evolution in the Richtmyer–Meshkov instability upon reshock.
Journal of Fluid Mechanics,
Vol. 975,
Issue. ,
Gattere, Federica
Chiarini, Alessandro
Gallorini, Emanuele
and
Quadrio, Maurizio
2023.
Structure function tensor equations with triple decomposition.
Journal of Fluid Mechanics,
Vol. 960,
Issue. ,
Ferguson, Kevin
and
Jacobs, Jeffrey W.
2024.
The influence of the shock-to-reshock time on the Richtmyer–Meshkov instability in reshock.
Journal of Fluid Mechanics,
Vol. 999,
Issue. ,
Yu, Dehai
and
Chen, Zheng
2024.
Premixed flame ignition: Theoretical development.
Progress in Energy and Combustion Science,
Vol. 104,
Issue. ,
p.
101174.
Cherry, Léa
Flamant, Gilles
and
Bataille, Françoise
2025.
Analytical developments for turbulent flows subjected to strong temperature gradients.
International Communications in Heat and Mass Transfer,
Vol. 162,
Issue. ,
p.
108550.
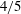 $4/5$-law with the same value of constant (
$4/5$-law with the same value of constant (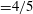 $=4/5$) appearing as the prefactor of the dissipation rate. The equation is employed to understand negative turbulent kinetic energy production in a
$=4/5$) appearing as the prefactor of the dissipation rate. The equation is employed to understand negative turbulent kinetic energy production in a 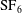 $\text{SF}_{6}$ turbulent round jet with an initial density ratio of 4.2. From a Reynolds-averaged Navier–Stokes (RANS) perspective, negative production means that the mean flow is strengthened at the expense of the energy of turbulent fluctuations. We show that the associated energy transfer is accomplished by the deformation of smaller turbulent eddies into large ones in the development region of the jet and is captured by the linear scale-by-scale energy transfer term in the VD K–H–M equation. The nonlinear transfer term of the VD K–H–M equation depicts a conventional forward cascade for all eddies having a size less than the Eulerian integral length scale, regardless of their orientation. The net effect is a retarded energy cascade in the non-Boussinesq jet that has not been accounted for by existing turbulence theories. Implications of this observation for turbulence modelling are discussed.
$\text{SF}_{6}$ turbulent round jet with an initial density ratio of 4.2. From a Reynolds-averaged Navier–Stokes (RANS) perspective, negative production means that the mean flow is strengthened at the expense of the energy of turbulent fluctuations. We show that the associated energy transfer is accomplished by the deformation of smaller turbulent eddies into large ones in the development region of the jet and is captured by the linear scale-by-scale energy transfer term in the VD K–H–M equation. The nonlinear transfer term of the VD K–H–M equation depicts a conventional forward cascade for all eddies having a size less than the Eulerian integral length scale, regardless of their orientation. The net effect is a retarded energy cascade in the non-Boussinesq jet that has not been accounted for by existing turbulence theories. Implications of this observation for turbulence modelling are discussed.

