Hostname: page-component-586b7cd67f-dsjbd Total loading time: 0 Render date: 2024-11-26T17:23:58.484Z Has data issue: false hasContentIssue false
  • English
  • Français

Is spontaneous generation of coherent baroclinic flows possible?

Published online by Cambridge University Press:  15 January 2019

Nikolaos A. Bakas Open the ORCID record for Nikolaos A. Bakas [Opens in a new window]  and
Petros J. Ioannou
Nikolaos A. Bakas*
Affiliation:
Laboratory of Meteorology and Climatology, Department of Physics, University of Ioannina, 45110 Ioannina, Greece
Petros J. Ioannou
Affiliation:
Department of Physics, National and Kapodistrian University of Athens, 15784 Athens, Greece
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Geophysical turbulence is observed to self-organize into large-scale flows such as zonal jets and coherent vortices. Previous studies of barotropic 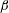$\unicode[STIX]{x1D6FD}$-plane turbulence have shown that coherent flows emerge from a background of homogeneous turbulence as a bifurcation when the turbulence intensity increases. The emergence of large-scale flows has been attributed to a new type of collective, symmetry-breaking instability of the statistical state dynamics of the turbulent flow. In this work, we extend the analysis to stratified flows and investigate turbulent self-organization in a two-layer fluid without any imposed mean north–south thermal gradient and with turbulence supported by an external random stirring. We use a second-order closure of the statistical state dynamics, that is termed S3T, with an appropriate averaging ansatz that allows the identification of statistical turbulent equilibria and their structural stability. The bifurcation of the statistically homogeneous equilibrium state to inhomogeneous equilibrium states comprising zonal jets and/or large-scale waves when the energy input rate of the excitation passes a critical threshold is analytically studied. Our theory predicts that there is a large bias towards the emergence of barotropic flows. If the scale of excitation is of the order of (or larger than) the deformation radius, the large-scale structures are barotropic. Mixed barotropic–baroclinic states with jets and/or waves arise when the excitation is at scales shorter than the deformation radius with the baroclinic component of the flow being subdominant for low energy input rates and insignificant for higher energy input rates. The predictions of the S3T theory are compared with nonlinear simulations. The theory is found to accurately predict both the critical transition parameters and the scales of the emergent structures but underestimates their amplitude.

JFM classification

Geophysical and Geological Flows: Geostrophic turbulence Nonlinear Dynamical Systems: Pattern formation
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 862 , 10 March 2019 , pp. 889 - 923
Copyright
© 2019 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Ait-Chaalal, F., Schneider, T., Meyer, B. & Marston, J. B. 2016 Cumulant expansions for atmospheric flows. New. J. Phys. 18 (2), 025019.Google Scholar
Bakas, N. A., Constantinou, N. C. & Ioannou, P. J. 2015 S3T stability of the homogeneous state of barotropic beta-plane turbulence. J. Atmos. Sci. 72 (5), 1689–1712.Google Scholar
Bakas, N. A. & Ioannou, P. J. 2013a Emergence of large scale structure in barotropic 𝛽-plane turbulence. Phys. Rev. Lett. 110, 224501.Google Scholar
Bakas, N. A. & Ioannou, P. J. 2013b On the mechanism underlying the spontaneous emergence of barotropic zonal jets. J. Atmos. Sci. 70 (7), 2251–2271.Google Scholar
Bakas, N. A. & Ioannou, P. J. 2014 A theory for the emergence of coherent structures in beta-plane turbulence. J. Fluid Mech. 740, 312–341.Google Scholar
Bakas, N. A. & Ioannou, P. J. 2019 Emergence of non-zonal coherent structures. In Zonal Jets (ed. Galperin, B. & Read, P. L.), chap. 27. Cambridge University Press, arXiv:1501.05280.Google Scholar
Bernstein, J. & Farrell, B. F. 2010 Low frequency variability in a turbulent baroclinic jet: eddy-mean flow interactions in a two-level model. J. Atmos. Sci. 67 (2), 452–467.Google Scholar
Bouchet, F., Marston, J. B. & Tangarife, T. 2018 Fluctuations and large deviations of Reynolds stresses in zonal jet dynamics. Phys. Fluids 30 (1), 015110.Google Scholar
Cehelsky, P. & Tung, K.-K. 1991 Nonlinear baroclinic adjustment. J. Atmos. Sci. 48, 1930–1947.Google Scholar
Chelton, D. B., Schlax, M. G., Samelson, R. M. & deSzoeke, R. A. 2007 Global observations of large oceanic eddies. Geophys. Res. Lett. 34, L12607.Google Scholar
Connaughton, C. P., Nadiga, B. T., Nazarenko, S. V. & Quinn, B. E. 2010 Modulational instability of Rossby and drift waves and generation of zonal jets. J. Fluid Mech. 645, 207–231.Google Scholar
Constantinou, N. C., Farrell, B. F. & Ioannou, P. J. 2014a Emergence and equilibration of jets in beta-plane turbulence: applications of stochastic structural stability theory. J. Atmos. Sci. 71 (5), 1818–1842.Google Scholar
Constantinou, N. C., Farrell, B. F. & Ioannou, P. J. 2016 Statistical state dynamics of jet-wave coexistence in barotropic beta-plane turbulence. J. Atmos. Sci. 73 (5), 2229–2253.Google Scholar
Constantinou, N. C., Lozano-Durán, A., Nikolaidis, M.-A., Farrell, B. F., Ioannou, P. J. & Jiménez, J. 2014b Turbulence in the highly restricted dynamics of a closure at second order: comparison with DNS. J. Phys.: Conf. Ser. 506, 012004.Google Scholar
Constantinou, N. C. & Parker, J. B. 2018 Magnetic suppression of zonal flows on a beta plane. Astrophys. J. 863 (1), 46.Google Scholar
DelSole, T. 1996 Can quasigeostrophic turbulence be modeled stochastically? J. Atmos. Sci. 53, 1617–1633.Google Scholar
Farrell, B. F., Gayme, D. F. & Ioannou, P. J. 2017 A statistical state dynamics approach to wall-turbulence. Phil. Trans. R. Soc. Lond. A 375 (2089), 20160081.Google Scholar
Farrell, B. F. & Ioannou, P. J. 2003 Structural stability of turbulent jets. J. Atmos. Sci. 60, 2101–2118.Google Scholar
Farrell, B. F. & Ioannou, P. J. 2007 Structure and spacing of jets in barotropic turbulence. J. Atmos. Sci. 64, 3652–3665.Google Scholar
Farrell, B. F. & Ioannou, P. J. 2008 Formation of jets by baroclinic turbulence. J. Atmos. Sci. 65, 3353–3375.Google Scholar
Farrell, B. F. & Ioannou, P. J. 2009a Emergence of jets from turbulence in the shallow-water equations on an equatorial beta plane. J. Atmos. Sci. 66, 3197–3207.Google Scholar
Farrell, B. F. & Ioannou, P. J. 2009b A stochastic structural stability theory model of the drift wave-zonal flow system. Phys. Plasmas 16, 112903.Google Scholar
Farrell, B. F. & Ioannou, P. J. 2017 Statistical state dynamics based theory for the formation and equilibration of Saturn’s north polar jet. Phys. Rev. Fluids 2 (7), 073801.Google Scholar
Farrell, B. F. & Ioannou, P. J. 2019 Statistical state dynamics: a new perspective on turbulence in shear flow. In Zonal Jets (ed. Galperin, B. & Read, P. L.), chap. 25. Cambridge University Press, arXiv:1412.8290.Google Scholar
Farrell, B. F., Ioannou, P. J., Jiménez, J., Constantinou, N. C., Lozano-Durán, A. & Nikolaidis, M.-A. 2016 A statistical state dynamics-based study of the structure and mechanism of large-scale motions in plane Poiseuille flow. J. Fluid Mech. 809, 290–315.Google Scholar
Fitzgerald, J. G. & Farrell, B. F. 2014 Mechanisms of mean flow formation and suppression in two-dimensional Rayleigh–Bénard convection. Phys. Fluids 26 (5), 054104.Google Scholar
Fitzgerald, J. G. & Farrell, B. F. 2018 Statistical state dynamics of vertically sheared horizontal flows in two-dimensional stratified turbulence. J. Fluid Mech. 854, 544–590.Google Scholar
Frishman, A. & Herbert, C. 2018 Turbulence statistics in a 2D vortex condensate. Phys. Rev. Lett. 120, 204505.Google Scholar
Galperin, B., Sukoriansky, S., Dikovskaya, N., Read, P. L., Yamazaki, Y. H. & Wordsworth, R. 2006 Anisotropic turbulence and zonal jets in rotating flows with a beta-effect. Nonlin Process. Geophys. 13, 83–98.Google Scholar
Galperin, B., Young, R. M. B., Sukoriansky, S., Dikovskaya, N., Read, P. L., Lancaster, A. L. & Armstrong, D. 2014 Cassini observations reveal a regime of zonostrophic macroturbulence on Jupiter. Icarus 229, 295–320.Google Scholar
Held, I. M. & Larichev, V. D. 1996 A scaling theory for horizontally homogeneous, baroclinically unstable flow on a beta plane. J. Atmos. Sci. 53, 946–952.Google Scholar
Hopf, E. 1952 Statistical hydromechanics and functional calculus. J. Ration. Mech. Anal. 1, 87–123.Google Scholar
Ingersoll, A. P. 1990 Atmospheric dynamics of the outer planets. Science 248, 308–315.Google Scholar
Kaspi, Y., Galanti, E., Hubbard, W. B., Stevenson, D. J., Bolton, S. J., Iess, L., Guillot, T., Bloxham, J., Connerney, J. E. P., Cao, H., Durante, D., Folkner, W. M., Helled, R., Ingersoll, A. P., Levin, S. M., Lunine, J. I., Miguel, Y., Militzer, B., Parisi, M. & Wahl, S. M. 2018 Jupiter’s atmospheric jet streams extend thousands of kilometres deep. Nature 555, 223 EP.Google Scholar
Kraichnan, R. H. 1964 Direct interaction approximation for shear and thermally driven turbulence. Phys. Fluids 7, 1048–1062.Google Scholar
Lilly, D. K. 1969 Numerical simulation of two-dimensional turbulence. Phys. Fluids 12, II240–II249.Google Scholar
Liu, J. & Schneider, T. 2015 Scaling of off-equatorial jets in giant planet atmospheres. J. Atmos. Sci. 72, 389–408.Google Scholar
Marston, J. B. 2010 Statistics of the general circulation from cumulant expansions. Chaos 20, 041107.Google Scholar
Marston, J. B., Chini, G. P. & Tobias, S. M. 2016 Generalized quasilinear approximation: application to zonal jets. Phys. Rev. Lett. 116 (21), 214501 EP–5.Google Scholar
Marston, J. B., Conover, E. & Schneider, T. 2008 Statistics of an unstable barotropic jet from a cumulant expansion. J. Atmos. Sci. 65 (6), 1955–1966.Google Scholar
Maximenko, N. A., Bang, B. & Sasaki, H. 2005 Observational evidence of alternating zonal jets in the world ocean. Geophys. Res. Lett. 32, L12607.Google Scholar
Monin, A. S. & Yaglom, A. M. 1973 Statistical Fluid Mechanics: Mechanics of Turbulence, vol. 1. The MIT Press.Google Scholar
Parker, J. B. & Krommes, J. A. 2013 Zonal flow as pattern formation. Phys. Plasmas 20, 100703.Google Scholar
Parker, J. B. & Krommes, J. A. 2014 Generation of zonal flows through symmetry breaking of statistical homogeneity. New J. Phys. 16 (3), 035006.Google Scholar
Parker, J. B. & Krommes, J. A. 2015 Zonal flow as pattern formation. In Zonal Jets: Phenomenology, Genesis, Physics (ed. Galperin, B. & Read, P. L.), chap. 5. Cambridge University Press.Google Scholar
Rhines, P. B. 1975 Waves and turbulence on a beta-plane. J. Fluid Mech. 69, 417–433.Google Scholar
Scott, R. K. & Dritschel, D. G. 2012 The structure of zonal jets in geostrophic turbulence. J. Fluid Mech. 711, 576–598.Google Scholar
Srinivasan, K. & Young, W. R. 2012 Zonostrophic instability. J. Atmos. Sci. 69 (5), 1633–1656.Google Scholar
Tobias, S. M., Dagon, K. & Marston, J. B. 2011 Astrophysical fluid dynamics via direct numerical simulation. Astrophys. J. 727, 127.Google Scholar
Vallis, G. K. & Maltrud, M. E. 1993 Generation of mean flows and jets on a beta-plane and over topography. J. Phys. Oceanogr. 23, 1346–1362.Google Scholar