Hostname: page-component-586b7cd67f-2brh9 Total loading time: 0 Render date: 2024-11-29T12:09:24.196Z Has data issue: false hasContentIssue false
  • English
  • Français

Inviscid instability of a stably stratified compressible boundary layer on an inclined surface

Published online by Cambridge University Press:  02 February 2012

Julien Candelier ,
Stéphane Le Dizès  and
Christophe Millet
Julien Candelier
Affiliation:
CEA, DAM, DIF, F-91297 Arpajon, France IRPHE, CNRS & Aix-Marseille University, 49 rue F. Joliot-Curie, F-13013 Marseille, France
Stéphane Le Dizès*
Affiliation:
IRPHE, CNRS & Aix-Marseille University, 49 rue F. Joliot-Curie, F-13013 Marseille, France
Christophe Millet
Affiliation:
CEA, DAM, DIF, F-91297 Arpajon, France
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

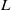The three-dimensional stability of an inflection-free boundary layer flow of length scale and maximum velocity 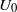in a stably stratified and compressible fluid of constant Brunt–Väisälä frequency 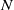, sound speed 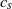and stratification length 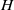is examined in an inviscid framework. The shear plane of the boundary layer is assumed to be inclined at an angle 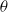with respect to the vertical direction of stratification. The stability analysis is performed using both numerical and theoretical methods for all the values of 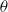and Froude number 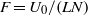. When non-Boussinesq and compressible effects are negligible ( 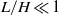and 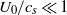), the boundary layer flow is found to be unstable for any 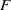as soon as 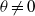. Compressible and non-Boussinesq effects are considered in the strongly stratified limit: they are shown to have no influence on the stability properties of an inclined boundary layer (when 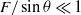). In this limit, the instability is associated with the emission of internal-acoustic waves.

JFM classification

Boundary Layers: Boundary layer stability Geophysical and Geological Flows: Stratified flows
Type
Papers
Information
Journal of Fluid Mechanics , Volume 694 , 10 March 2012 , pp. 524 - 539
Copyright
Copyright © Cambridge University Press 2012

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1. Bakas, N. A. & Farrell, B. F. 2009 Gravity waves in a horizontal shear flow. Part II. Interaction between gravity waves and potential vorticity perturbations. J. Phys. Oceanogr. 39, 497–511.Google Scholar
2. Balmforth, N. J. 1999 Shear instability in shallow water. J. Fluid Mech. 387, 97–127.Google Scholar
3. Basovich, A. Y. & Tsimring, L. S. 1984 Internal waves in a horizontally inhomogeneous flow. J. Fluid Mech. 142, 223–249.CrossRefGoogle Scholar
4. Billant, P. & Le Dizès, S. 2009 Waves on a columnar vortex in a strongly stratified fluid. Phys. Fluids 21, 106602.Google Scholar
5. Broadbent, E. & Moore, D. W. 1979 Acoustic destabilization of vortices. Phil. Trans. R. Soc. A 290, 353–371.Google Scholar
6. Candelier, J. 2010 Instabilités radiatives des jets et couches limites atmosphériques. PhD thesis, Aix-Marseille Université, Marseille.Google Scholar
7. Candelier, J., Le Dizès, S. & Millet, C. 2011 Shear instability in a stratified fluid when shear and stratification are not aligned. J. Fluid Mech. 685, 191–201.CrossRefGoogle Scholar
8. Chimonas, G. 1974 Consideration of the stability of certain heterogeneous shear flows including some inflexion-free profiles. J. Fluid Mech. 65, 65–69.CrossRefGoogle Scholar
9. Chimonas, G. 2002 On internal gravity waves associated with the stable boundary layer. Boundary-Layer Meteorol. 102, 139–155.Google Scholar
10. Churilov, S. M. 2005 Stability analysis of stratified shear flows with a monotonic velocity profile without inflection points. J. Fluid Mech. 539, 25–55.CrossRefGoogle Scholar
11. Churilov, S. M. 2008 Stability analysis of stratified shear flows with a monotonic velocity profile without inflection points. Part 2. Continuous density variation. J. Fluid Mech. 617, 301–326.Google Scholar
12. Davis, P. A. & Peltier, W. R. 1976 Resonant parallel shear instability in the stratified planetary boundary layer. J. Atmos. Sci. 33, 1287–1300.Google Scholar
13. Drazin, P. G. & Reid, W. H. 1981 Hydrodynamic Stability. Cambridge University Press.Google Scholar
14. Dritschel, D. G. & Vanneste, J. 2006 Instability of a shallow-water potential-vorticity front. J. Fluid Mech. 561, 237–254.Google Scholar
15. Dunn, W. & Lin, C. 1955 On the stability of the laminar boundary layer in a compressible fluid. J. Aero. Sci. 22.CrossRefGoogle Scholar
16. Eckart, C. 1960 Hydrodynamics of Oceans and Atmospheres. Pergamon.Google Scholar
17. Ford, R. 1994 The instability of an axisymmetric vortex with monotonic potential vorticity in rotating shallow water. J. Fluid Mech. 280, 303–334.CrossRefGoogle Scholar
18. Frehlich, R., Meillier, Y. & Jensen, M. L. 2008 Measurements of boundary layer profiles with in situ sensors and Doppler lidar. J. Atmos. Ocean. Technol. 25, 1328–1340.Google Scholar
19. Gossard, E. E. & Hooke, W. H. 1975 Waves in the Atmosphere. Elsevier.Google Scholar
20. Houghton, J. T. 1986 The Physics of Atmosphere. Cambridge University Press.Google Scholar
21. Howard, L. N. 1961 Note on a paper of John W. Miles. J. Fluid Mech. 10, 509–512.Google Scholar
22. Kopev, V. F. & Leontev, E. A. 1983 Acoustic instability of an axial vortex. Sov. Phys. Acoust. 29, 111–115.Google Scholar
23. Le Dizès, S. & Billant, P. 2009 Radiative instability in stratified vortices. Phys. Fluids 21, 096602.Google Scholar
24. Le Dizès, S. & Riedinger, X. 2010 The strato-rotational instability of Taylor–Couette and Keplerian flows. J. Fluid Mech. 660, 147–161.CrossRefGoogle Scholar
25. Lees, L. & Lin, C. C. 1946 Investigation of the stability of the laminar boundary layer in a compressible fluid. NACA Technical Note 1115.Google Scholar
26. Lees, L. & Reshotko, E. 1962 Stability of the compressible laminar boundary layer. J. Fluid Mech. 12, 555–590.Google Scholar
27. Lindzen, R. S. & Barker, J. W. 1985 Instability and wave over-reflection in stably stratified shear flow. J. Fluid Mech. 151, 189–217.CrossRefGoogle Scholar
28. Luo, K. H. & Sandham, N. D. 1997 Instability of vortical and acoustic modes in supersonic round jets. Phys. Fluids 9, 1003–1013.Google Scholar
29. Mack, L. M. 1965 The stability of the compressible laminar boundary layer according to a direct numerical solution. In Recent Developments in Boundary Layer Research, AGARDograph , vol. 97, pp. 329–362.Google Scholar
30. Mack, L. M. 1969 Boundary layer stability theory. Tech. Rep. JPL-900-277-REV-A, Jet Propulsion Laboratory.Google Scholar
31. Mack, L. M. 1990 On the inviscid acoustic-mode instability of supersonic shear flows. Part 1. Two-dimensional waves. Theor. Comput. Fluid Dyn. 2, 97–123.Google Scholar
32. Mastrantonio, G., Einaudi, F., Fua, D. & Lalas, D. P. 1976 Generation of gravity waves by jet streams in the atmosphere. J. Atmos. Sci. 33, 1730–1738.2.0.CO;2>CrossRefGoogle Scholar
33. Miles, J. W. 1961 On the stability of heterogeneous shear flows. J. Fluid Mech. 10, 496–508.Google Scholar
34. Parras, L. & Le Dizès, S. 2010 Temporal instability modes of supersonic round jets. J. Fluid Mech. 660, 173–196.Google Scholar
35. Riedinger, X., Le Dizès, S. & Meunier, P. 2010a Viscous stability properties of a Lamb–Oseen vortex in a stratified fluid. J. Fluid Mech. 645, 255–278.Google Scholar
36. Riedinger, X., Le Dizès, S. & Meunier, P. 2011 Radiative instability of the flow around a rotating cylinder in a stratified fluid. J. Fluid Mech. 672, 130–146.Google Scholar
37. Riedinger, X., Meunier, P. & Le Dizès, S. 2010b Instability of a vertical columnar vortex in a stratified fluid. Exp. Fluids 49, 673–681.Google Scholar
38. Satomura, T. 1981 An investigation of shear instability in a shallow water. J. Met. Soc. Japan 59, 148–167.Google Scholar
39. Schecter, D. A. & Montgomery, M. T. 2004 Damping and pumping of a vortex Rossby wave in a monotonic cyclone: critical layer stirring versus inertia–buoyancy wave emission. Phys. Fluids 16, 1334–1348.CrossRefGoogle Scholar
40. Schmid, P. J. & Henningson, D. S. 2001 Stability and transition in shear flows. In Applied Mathematical Sciences, vol. 142. Springer.Google Scholar
41. Smyth, W. & Peltier, W. 1989 The transition between Kelvin–Helmholtz and Holmboe instability: an investigation of the overreflection hypothesis. J. Atmos. Sci. 46 (24), 3698–3720.2.0.CO;2>CrossRefGoogle Scholar
42. Takehiro, S.-I. & Hayashi, Y.-Y. 1992 Over-reflection and shear instability in a shallow-water model. J. Fluid Mech. 236, 259–279.Google Scholar
43. Tam, C. K. W. & Hu, F. Q. 1989a The instability and acoustic wave modes of supersonic mixing layers inside a rectangular channel. J. Fluid Mech. 203, 51–76.Google Scholar
44. Tam, C. K. W. & Hu, F. Q. 1989b On the three families of instability waves of high-speed jets. J. Fluid Mech. 201, 447–483.CrossRefGoogle Scholar
45. Watada, S. 2009 Radiation of acoustic and gravity waves and propagation of boundary waves in the stratified fluid from a time-varying bottom boundary. J. Fluid Mech. 627, 361–377.Google Scholar