Hostname: page-component-78c5997874-m6dg7 Total loading time: 0 Render date: 2024-11-05T05:09:11.038Z Has data issue: false hasContentIssue false
  • English
  • Français

Investigation of the roughness-induced transition: global stability analyses and direct numerical simulations

Published online by Cambridge University Press:  04 November 2014

Jean-Christophe Loiseau ,
Jean-Christophe Robinet ,
Stefania Cherubini  and
Emmanuel Leriche
Jean-Christophe Loiseau*
Affiliation:
Laboratoire DynFluid, Arts et Métiers ParisTech, 151 boulevard de l’Hôpital, 75013 Paris, France Laboratoire de Mécanique de Lille, Université Lille 1, Boulevard Paul Langevin, 59655 Villeneuve d’Ascq, France
Jean-Christophe Robinet
Affiliation:
Laboratoire DynFluid, Arts et Métiers ParisTech, 151 boulevard de l’Hôpital, 75013 Paris, France
Stefania Cherubini
Affiliation:
Laboratoire DynFluid, Arts et Métiers ParisTech, 151 boulevard de l’Hôpital, 75013 Paris, France
Emmanuel Leriche
Affiliation:
Laboratoire de Mécanique de Lille, Université Lille 1, Boulevard Paul Langevin, 59655 Villeneuve d’Ascq, France
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The linear global instability and resulting transition to turbulence induced by an isolated cylindrical roughness element of height 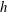$h$ and diameter 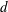$d$ immersed within an incompressible boundary layer flow along a flat plate is investigated using the joint application of direct numerical simulations and fully three-dimensional global stability analyses. For the range of parameters investigated, base flow computations show that the roughness element induces a wake composed of a central low-speed region surrounded by a three-dimensional shear layer and a pair of low- and high-speed streaks on each of its sides. Results from the global stability analyses highlight the unstable nature of the central low-speed region and its crucial importance in the laminar–turbulent transition process. It is able to sustain two different global instabilities: a sinuous and a varicose one. Each of these globally unstable modes is related to a different physical mechanism. While the varicose mode has its root in the instability of the whole three-dimensional shear layer surrounding the central low-speed region, the sinuous instability turns out to be similar to the von Kármán instability in the two-dimensional cylinder wake and has its root in the lateral shear layers of the separated zone. The aspect ratio of the roughness element plays a key role on the selection of the dominant instability: whereas the flow over thin cylindrical roughness elements transitions due to a sinuous instability of the near-wake region, for larger roughness elements the varicose instability of the central low-speed region turns out to be the dominant one. Direct numerical simulations of the flow past an aspect ratio 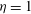${\it\eta}=1$ (with 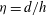${\it\eta}=d/h$) roughness element sustaining only the sinuous instability have revealed that the bifurcation occurring in this particular case is supercritical. Finally, comparison of the transition thresholds predicted by global linear stability analyses with the von Doenhoff–Braslow transition diagram provides qualitatively good agreement.

JFM classification

Boundary Layers: Boundary Layers Instability: Instability Instability: Transition to turbulence
Type
Papers
Information
Journal of Fluid Mechanics , Volume 760 , 10 December 2014 , pp. 175 - 211
Check for updates
Copyright
© 2014 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Acarlar, M. & Smith, C. 1987 A study of hairpin vortices in a laminar boundary layer. Part 1. Hairpin vortices generated by a hemisphere protuberance. J. Fluid Mech. 175, 1–41.CrossRefGoogle Scholar
Akervik, E., Brandt, L., Henningson, D. S., Hoepffner, J., Marxen, O. & Schlatter, P. 2006 Steady solutions of the Navier–Stokes equations by selective frequency damping. Phys. Fluids 18, 068102.Google Scholar
Andersson, P., Brandt, L., Bottaro, A. & Henningson, D. S. 2001 On the breakdown of boundary layer streaks. J. Fluid Mech. 428, 29–60.CrossRefGoogle Scholar
Arnal, D., Houdeville, R., Séraudie, A. & Vermeersch, O.2011 Overview of laminar-turbulent transition investigations at ONERA toulouse. In 41st AIAA Fluid Dynamics Conference, Honolulu, HI, AIAA 2011-3074.Google Scholar
Asai, M., Konishi, Y., Oizumi, Y. & Nishioka, M. 2007 Growth and breakdown of low-speed streaks leading to wall turbulence. J. Fluid Mech. 586, 371–396.Google Scholar
Asai, M., Minagawa, M. & Nishioka, M. 2002 The instability and breakdown of a near-wall low-speed streak. J. Fluid Mech. 455, 289–314.CrossRefGoogle Scholar
Bagheri, S., Akervik, E., Brandt, L. & Henningson, D. S. 2009a Matrix-free methods for the stability and control of boundary layers. AIAA J. 47 (5), 1057–1068.CrossRefGoogle Scholar
Bagheri, S., Schlatter, P., Schmid, P. J. & Henningson, D. S. 2009b Global stability of a jet in crossflow. J. Fluid Mech. 624, 33–44.Google Scholar
Baker, C. J. 1978 The laminar horseshoe vortex. J. Fluid Mech. 95, 347–367.Google Scholar
Balakumar, P. & Kegerise, M.2013 Roughness induced transition in a supersonic boundary layer. In 43rd AIAA Fluid Dynamics Conference, San Diego, CA.Google Scholar
Barkley, D., Blackburn, H. M. & Sherwin, S. J. 2008 Direct optimal growth analysis for timesteppers. Intl J. Methods Fluids 57, 1435–1458.Google Scholar
Beaudoin, J.-Fr.2004 Contrôle actif d’écoulement en aérodynamique automobile. PhD thesis, Ecole des Mines de Paris.Google Scholar
Bernardini, M., Pirozzoli, S. & Orlandi, P. 2012 Compressibility effects on roughness-induced boundary layer transition. Intl J. Heat Fluid Flow 35, 45–51.CrossRefGoogle Scholar
Brandt, L. 2007 Numerical studies of the instability and breakdown of a boundary-layer low-speed streak. Eur. J. Mech. (B/Fluids) 26 (1), 64–82.Google Scholar
Cherubini, S., De Tullio, M. D., De Palma, P. & Pascazio, G. 2013 Transient growth in the flow past a three-dimensional smooth roughness element. J. Fluid Mech. 724, 642–670.CrossRefGoogle Scholar
Chomaz, J. M. 2005 Global instabilities in spatially developing flows: non-normality and nonlinearity. Annu. Rev. Fluid Mech. 37, 357–392.Google Scholar
Cossu, C. & Brandt, L. 2004 On Tollmien–Schlichting-like waves in streaky boundary layers. Eur. J. Mech. (B/Fluids) 23 (6), 815–833.Google Scholar
Denissen, N. A. & White, E. B. 2008 Roughness-induced bypass transition revisited. AIAA J. 46 (7), 1874–1877.Google Scholar
Denissen, N. A. & White, E. B. 2009 Continuous spectrum analysis of roughness-induced transient growth. Phys. Fluids 21, 114105.Google Scholar
Denissen, N. A. & White, E. B. 2013 Secondary instability of roughness-induced transient growth. Phys. Fluids 25, 114108.Google Scholar
von Doenhoff, A. E. & Braslow, A. L. 1961 The effect of distributed roughness on laminar flow. In Boundary Layer Control (ed. Lachmann), vol. 2, pp. 657–681. Pergamon.Google Scholar
Edwards, W. S., Tuckerman, L. S., Friesner, R. A. & Sorensen, D. C. 1994 Krylov methods for the incompressible Navier–Stokes equations. J. Comput. Phys. 110, 82–102.CrossRefGoogle Scholar
Ergin, F. G. & White, E. B. 2006 Unsteady and transitional flows behind roughness elements. AIAA J. 44 (11), 2504–2514.Google Scholar
Fischer, P. & Choudhari, M.2004 Numerical simulation of roughness induced transient growth in a laminar boundary layer. In 34th AIAA Fluid Dynamics Conference, Portland, Oregon, AIAA 2004-2539.Google Scholar
Fischer, P. F., Lottes, J. W. & Kerkemeir, S. G.2008 Nek5000 Web Pages. Available at: http://nek5000.mcs.anl.gov.Google Scholar
Fransson, J. H. M., Brandt, L., Talamelli, A. & Cossu, C. 2004 Experimental and theoretical investigation of the nonmodal growth of steady streaks in a flat plate boundary layer. Phys. Fluids 10, 3627–3638.CrossRefGoogle Scholar
Fransson, J. H., Brandt, L., Talamelli, A. & Cossu, C. 2005 Experimental study of the stabilization of Tollmien–Schlichting waves by finite amplitude streaks. Phys. Fluids 17, 054110.Google Scholar
Fransson, J. H. M., Talamelli, A., Brandt, L. & Cossu, C. 2006 Delaying transition to turbulence by a passive mechanism. Phys. Rev. Lett. 96, 064501.Google Scholar
Giannetti, F. & Luchini, P. 2007 Structural sensitivity of the first instability of the cylinder wake. J. Fluid Mech. 581, 167–197.Google Scholar
Gregory, N. & Walker, W. S.1955 The effect of transition of isolated surface excrescences in the boundary layer. Tech Rep. R. & M. 2779. Aeronautical Research Council.Google Scholar
Ilak, M., Schlatter, P., Bagheri, S. & Henningson, D. S. 2012 Bifurcation and stability analysis of a jet in cross-flow: onset of global instability at a low velocity ratio. J. Fluid Mech. 686, 94–121.CrossRefGoogle Scholar
Iyer, P. S. & Mahesh, K. 2013 High-speed boundary-layer transition induced by a discrete roughness element. J. Fluid Mech. 729, 524–562.Google Scholar
Jeong, J. & Hussain, F. 1995 On the identification of a vortex. J. Fluid Mech. 285, 69–94.Google Scholar
Joslin, R. D. & Grosch, C. E. 1995 Growth characterisitcs downstream of a shallow bump: computation and experiments. Phys. Fluids 7, 3042–3047.Google Scholar
Klebanoff, P. S. & Tidstrom, K. D. 1972 Mechanism by which a two-dimensional roughness element induces boundary-layer transition. Phys. Fluids 15, 1173–1188.Google Scholar
Konishi, Y. & Asai, M. 2004 Experimental investigation of the instability of spanwise-periodic low-speed streaks. Fluid Dyn. Res. 34 (5), 299–315.Google Scholar
Landahl, M. T. 1990 On sublayer streaks. J. Fluid Mech. 212, 593–614.CrossRefGoogle Scholar
Loiseau, J.-Ch., Cherubini, S., Robinet, J.-Ch. & Leriche, E. 2013 Influence of the shape on the roughness-induced transition. In Instability and Control of Massively Separated Flows (ed. Theofilis, V. & Soria, J.), Fluid Mechanics and its Applications, vol. 107. Springer.Google Scholar
Luchini, P. & Bottaro, A. 2014 Adjoint equations in stability analysis. Annu. Rev. Fluid Mech. 46, 493–517.Google Scholar
Marquet, O., Sipp, D. & Jacquin, L. 2008 Sensitivity analysis and passive control of cylinder flow. J. Fluid Mech. 615, 221–252.Google Scholar
Perraud, J., Arnal, D., Séraudie, A. & Tran, D.2004 Laminar-turbulent transition on aerodynamics surfaces with imperfections. In Proceeding of RTO AVT-111 Symposium, Prague, Czech Republic.Google Scholar
Piot, E., Casalis, G. & Rist, U. 2008 Stability of the laminar boundary layer flow encountering a row of roughness elements: biglobal stability approach and DNS. Eur. J. Mech. (B/Fluids) 27 (6), 684–706.Google Scholar
Sakamoto, H. & Arie, M. 1983 Vortex shedding from a rectangular prism and a circular cylinder placed vertically in a turbulent boundary layer. J. Fluid Mech. 126, 147–165.Google Scholar
Sedney, R. 1972 A survey of the effects of small protuberanecs on boundary-layer flows. AIAA J. 11 (6), 782–792.Google Scholar
Stephani, K. A. & Goldstein, D. B.2009 DNS study of transient disturbance growth and bypass transition due to realistic roughness. In 47th AIAA Aerospace Sciences Meeting Including the New Horizons Forum and Aerospace Exposition, Orlando, FL, AIAA 2009-585.Google Scholar
Subbareddy, P. K., Bartkowicz, M. D. & Candler, G. V. 2014 Direct numerical simulation of high-speed transition due to an isolated roughness element. J. Fluid Mech. 748, 848–878.CrossRefGoogle Scholar
Tani, I., Komoda, H. & Komatsu, Y.1962 Boundary-layer transition by isolated roughness. Tech Rep. 375. Aeronautical Research Institute, University of Tokyo.Google Scholar
Tufo, H. M., Fischer, P. F., Papka, M. E. & Blom, K.1999 Numerical simulation and immersive visualization of hairpin vortices. In ACM/IEEE SC99 Conf. on High Performances Networking and Computing.Google Scholar
de Tullio, N., Paredes, P., Sandham, N. D. & Theofilis, V. 2013 Laminar-turbulent transition induced by discrete roughness element in a supersonic boundary layer. J. Fluid Mech. 735, 613–646.Google Scholar
Tumin, A. & Reshotko, E. 2005 Receptivity of a boundary-layer flow to a three-dimensional hump at finite Reynolds numbers. Phys. Fluids 17, 094101.Google Scholar
Vermeersch, O.2009 Etude et modélisation du phénomène de croissance transition pour des couches limites incompressibles et compressibles. PhD thesis, ISAE, Toulouse.Google Scholar
Zhou, Z., Wang, Z. & Fan, J. 2010 Direct numerical simulation of the transional boundary-layer flow induced by an isolated hemispherical roughness element. Comput. Meth. Appl. Mech. Engng 199, 1573–1582.Google Scholar