Hostname: page-component-586b7cd67f-t7czq Total loading time: 0 Render date: 2024-11-26T06:09:30.378Z Has data issue: false hasContentIssue false
  • English
  • Français

Investigation of high-pressure turbulent jets using direct numerical simulation

Published online by Cambridge University Press:  13 July 2021

Nek Sharan Open the ORCID record for Nek Sharan [Opens in a new window]  and
Josette Bellan Open the ORCID record for Josette Bellan [Opens in a new window]
Nek Sharan
Affiliation:
Department of Mechanical and Civil Engineering, California Institute of Technology, Pasadena, CA91125, USA
Josette Bellan*
Affiliation:
Department of Mechanical and Civil Engineering, California Institute of Technology, Pasadena, CA91125, USA Jet Propulsion Laboratory, California Institute of Technology, Pasadena, CA91109, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

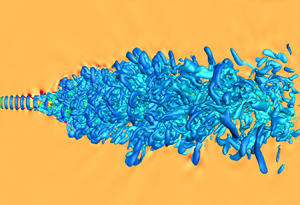
Direct numerical simulations of free round jets at a Reynolds number ($Re_{D}$) of $5000$, based on jet diameter ($D$) and jet-exit bulk velocity ($U_{e}$), are performed to study jet turbulence characteristics at supercritical pressures. The jet consists of nitrogen ($\mathrm {N}_{2}$) that is injected into $\mathrm {N}_{2}$ at the same temperature. To understand turbulent mixing, a passive scalar is transported with the flow at unity Schmidt number. Two sets of inflow conditions that model jets issuing from either a smooth contraction nozzle (laminar inflow) or a long pipe nozzle (turbulent inflow) are considered. By changing one parameter at a time, the simulations examine the jet-flow sensitivity to the thermodynamic condition (characterized in terms of the compressibility factor ($Z$) and the normalized isothermal compressibility), inflow condition and ambient pressure ($p_{\infty }$) spanning perfect- to real-gas conditions. The inflow affects flow statistics in the near field (containing the potential core closure and the transition region) as well as further downstream (containing fully developed flow with self-similar statistics) at both atmospheric and supercritical $p_{\infty }$. The sensitivity to inflow is larger in the transition region, where the laminar-inflow jets exhibit dominant coherent structures that produce higher mean strain rates and higher turbulent kinetic energy than in turbulent-inflow jets. Decreasing $Z$ at a fixed supercritical $p_{\infty }$ enhances pressure and density fluctuations (non-dimensionalized by local mean pressure and density, respectively), but the effect on velocity fluctuations depends also on the local flow dynamics. When $Z$ is reduced, large mean strain rates in the transition region of laminar-inflow jets significantly enhance velocity fluctuations (non-dimensionalized by local mean velocity) and scalar mixing, whereas the effects are minimal in jets from turbulent inflow.

JFM classification

Mathematical Foundations: General fluid mechanics Mixing: Turbulent mixing
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 922 , 10 September 2021 , A24
Check for updates
Copyright
© The Author(s), 2021. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

‡

Present address: CCS-2, Los Alamos National Laboratory, Los Alamos, NM 87544, USA.

References

REFERENCES

Baab, S., Förster, F.J., Lamanna, G. & Weigand, B. 2016 Speed of sound measurements and mixing characterization of underexpanded fuel jets with supercritical reservoir condition using laser-induced thermal acoustics. Exp. Fluids 57 (11), 1–13.CrossRefGoogle Scholar
Baab, S., Steinhausen, C., Lamanna, G., Weigand, B. & Förster, F.J. 2018 A quantitative speed of sound database for multi-component jet mixing at high pressure. Fuel 233, 918–925.CrossRefGoogle Scholar
Balaras, E., Piomelli, U. & Wallace, J.M. 2001 Self-similar states in turbulent mixing layers. J. Fluid Mech. 446, 1–24.CrossRefGoogle Scholar
Banuti, D.T., Raju, M. & Ihme, M. 2017 Similarity law for Widom lines and coexistence lines. Phys. Rev. E 95 (5), 052120.CrossRefGoogle ScholarPubMed
Bodony, D.J. 2006 Analysis of sponge zones for computational fluid mechanics. J. Comput. Phys. 212 (2), 681–702.CrossRefGoogle Scholar
Boersma, B.J., Brethouwer, G. & Nieuwstadt, F. 1998 A numerical investigation on the effect of the inflow conditions on the self-similar region of a round jet. Phys. Fluids 10 (4), 899–909.CrossRefGoogle Scholar
Chehroudi, B., Talley, D. & Coy, E. 2002 Visual characteristics and initial growth rates of round cryogenic jets at subcritical and supercritical pressures. Phys. Fluids 14 (2), 850–861.CrossRefGoogle Scholar
Dowling, D.R. & Dimotakis, P.E. 1990 Similarity of the concentration field of gas-phase turbulent jets. J. Fluid Mech. 218, 109–141.CrossRefGoogle Scholar
Ebrahimi, I. & Kleine, R. 1977 Konzentrationsfelder in isothermen luft-freistrahlen. Forsch. Ingen. A 43 (1), 25–30.CrossRefGoogle Scholar
Eggels, J., Unger, F., Weiss, M.H., Westerweel, J., Adrian, R.J., Friedrich, R. & Nieuwstadt, F. 1994 Fully developed turbulent pipe flow: a comparison between direct numerical simulation and experiment. J. Fluid Mech. 268, 175–210.CrossRefGoogle Scholar
Falgout, Z., Rahm, M., Wang, Z. & Linne, M. 2015 Evidence for supercritical mixing layers in the ECN Spray A. Proc. Combust. Inst. 35 (2), 1579–1586.CrossRefGoogle Scholar
Freund, J.B., Lele, S.K. & Moin, P. 2000 Compressibility effects in a turbulent annular mixing layer. Part 1. Turbulence and growth rate. J. Fluid Mech. 421, 229–267.CrossRefGoogle Scholar
Gao, W., Lin, Y., Hui, X., Zhang, C. & Xu, Q. 2019 Injection characteristics of near critical and supercritical kerosene into quiescent atmospheric environment. Fuel 235, 775–781.CrossRefGoogle Scholar
George, W.K. 1989 The self-preservation of turbulent flows and its relation to initial conditions and coherent structures. In Advances in Turbulence (ed. Arndt, R. & George, W.K.), pp. 39–73. Hemisphere.Google Scholar
George, W.K. & Davidson, L. 2004 Role of initial conditions in establishing asymptotic flow behavior. AIAA J. 42 (3), 438–446.CrossRefGoogle Scholar
Ghosal, S. & Rogers, M.M. 1997 A numerical study of self-similarity in a turbulent plane wake using large-eddy simulation. Phys. Fluids 9 (6), 1729–1739.CrossRefGoogle Scholar
Gnanaskandan, A. & Bellan, J. 2017 Numerical simulation of jet injection and species mixing under high-pressure conditions. J. Phys. 821, 012020.Google Scholar
Gnanaskandan, A. & Bellan, J. 2018 Side-jet effects in high-pressure turbulent flows: direct numerical simulation of nitrogen injected into carbon dioxide. J. Supercrit. Fluids 140, 165–181.CrossRefGoogle Scholar
Grinstein, F.F. 2001 Vortex dynamics and entrainment in rectangular free jets. J. Fluid Mech. 437, 69–101.CrossRefGoogle Scholar
Harstad, K.G., Miller, R.S. & Bellan, J. 1997 Efficient high-pressure state equations. AIChE J. 43 (6), 1605–1610.CrossRefGoogle Scholar
Ho, C.M. & Nosseir, N.S. 1981 Dynamics of an impinging jet. Part 1. The feedback phenomenon. J. Fluid Mech. 105, 119–142.CrossRefGoogle Scholar
Husain, Z.D. & Hussain, A.K.M.F. 1979 Axisymmetric mixing layer: influence of the initial and boundary conditions. AIAA J. 17 (1), 48–55.CrossRefGoogle Scholar
Hussein, H.J., Capp, S.P. & George, W.K. 1994 Velocity measurements in a high-Reynolds-number, momentum-conserving, axisymmetric, turbulent jet. J. Fluid Mech. 258, 31–75.CrossRefGoogle Scholar
Kennedy, C.A. & Carpenter, M.H. 1994 Several new numerical methods for compressible shear-layer simulations. Appl. Numer. Maths 14 (4), 397–433.CrossRefGoogle Scholar
Klein, M., Sadiki, A. & Janicka, J. 2003 A digital filter based generation of inflow data for spatially developing direct numerical or large eddy simulations. J. Comput. Phys. 186 (2), 652–665.CrossRefGoogle Scholar
Lele, S.K. 1994 Compressibility effects on turbulence. Annu. Rev. Fluid Mech. 26 (1), 211–254.CrossRefGoogle Scholar
Lemmon, E.W., et al. 2010 NIST standard reference database 23. NIST Reference Fluid Thermodynamic and Transport Properties – REFPROP, Version 9, 55.Google Scholar
Lodato, G., Domingo, P. & Vervisch, L. 2008 Three-dimensional boundary conditions for direct and large-eddy simulation of compressible viscous flows. J. Comput. Phys. 227 (10), 5105–5143.CrossRefGoogle Scholar
Lubbers, C.L., Brethouwer, G. & Boersma, B.J. 2001 Simulation of the mixing of a passive scalar in a round turbulent jet. Fluid Dyn. Res. 28 (3), 189–208.CrossRefGoogle Scholar
Lund, T.S., Wu, X. & Squires, K.D. 1998 Generation of turbulent inflow data for spatially-developing boundary layer simulations. J. Comput. Phys. 140 (2), 233–258.CrossRefGoogle Scholar
Masi, E., Bellan, J., Harstad, K.G. & Okong'o, N.A. 2013 Multi-species turbulent mixing under supercritical-pressure conditions: modelling, direct numerical simulation and analysis revealing species spinodal decomposition. J. Fluid Mech. 721, 578–626.CrossRefGoogle Scholar
Mattner, T.W. 2011 Large-eddy simulations of turbulent mixing layers using the stretched-vortex model. J. Fluid Mech. 671, 507–534.CrossRefGoogle Scholar
Mayer, W., Schik, A., Axel, H., Vielle, B., Chauveau, C., G-okalp, I., Talley, D.G. & Woodward, R.D. 1998 Atomization and breakup of cryogenic propellants under high-pressure subcritical and supercritical conditions. J. Propul. Power 14 (5), 835–842.CrossRefGoogle Scholar
Mayer, W., Telaar, J., Branam, R., Schneider, G. & Hussong, J. 2003 Raman measurements of cryogenic injection at supercritical pressure. Heat Mass Transfer 39 (8–9), 709–719.CrossRefGoogle Scholar
Mi, J., Nobes, D.S. & Nathan, G.J. 2001 Influence of jet exit conditions on the passive scalar field of an axisymmetric free jet. J. Fluid Mech. 432, 91–125.CrossRefGoogle Scholar
Michalke, A. 1984 Survey on jet instability theory. Prog. Aerosp. Sci. 21, 159–199.CrossRefGoogle Scholar
Morris, P.J. 1983 Viscous stability of compressible axisymmetric jets. AIAA J. 21 (4), 481–482.CrossRefGoogle Scholar
Muthukumaran, C.K. & Vaidyanathan, A. 2016 a Initial instability of round liquid jet at subcritical and supercritical environments. Phys. Fluids 28 (7), 074104.CrossRefGoogle Scholar
Muthukumaran, C.K. & Vaidyanathan, A. 2016 b Mixing nature of supercritical jet in subcritical and supercritical conditions. J. Propul. Power 33 (4), 842–857.CrossRefGoogle Scholar
Newman, J.A. & Brzustowski, T.A. 1971 Behavior of a liquid jet near the thermodynamic critical region. AIAA J. 9 (8), 1595–1602.CrossRefGoogle Scholar
Okong'o, N. & Bellan, J. 2002 a Consistent boundary conditions for multicomponent real gas mixtures based on characteristic waves. J. Comput. Phys. 176 (2), 330–344.CrossRefGoogle Scholar
Okong'o, N.A. & Bellan, J. 2002 b Direct numerical simulation of a transitional supercritical binary mixing layer: heptane and nitrogen. J. Fluid Mech. 464, 1–34.CrossRefGoogle Scholar
Okong'o, N.A., Harstad, K. & Bellan, J. 2002 Direct numerical simulations of O2/H2 temporal mixing layers under supercritical conditions. AIAA J. 40 (5), 914–926.CrossRefGoogle Scholar
Oschwald, M. & Schik, A. 1999 Supercritical nitrogen free jet investigated by spontaneous raman scattering. Exp. Fluids 27 (6), 497–506.CrossRefGoogle Scholar
Panchapakesan, N.R. & Lumley, J.L. 1993 Turbulence measurements in axisymmetric jets of air and helium. Part 1. Air jet. J. Fluid Mech. 246, 197–223.CrossRefGoogle Scholar
Pantano, C. & Sarkar, S. 2002 A study of compressibility effects in the high-speed turbulent shear layer using direct simulation. J. Fluid Mech. 451, 329–371.CrossRefGoogle Scholar
Papamoschou, D. & Roshko, A. 1988 The compressible turbulent shear layer: an experimental study. J. Fluid Mech. 197, 453–477.CrossRefGoogle Scholar
Poinsot, T.J. & Lele, S.K. 1992 Boundary conditions for direct simulations of compressible viscous flows. J. Comput. Phys. 101 (1), 104–129.CrossRefGoogle Scholar
Poling, B.E., et al. 2001 The Properties of Gases and Liquids, vol. 5. McGraw-Hill.Google Scholar
Poursadegh, F., Lacey, J.S., Brear, M.J. & Gordon, R.L. 2017 On the fuel spray transition to dense fluid mixing at reciprocating engine conditions. Energy Fuels 31 (6), 6445–6454.CrossRefGoogle Scholar
Richards, C.D. & Pitts, W.M. 1993 Global density effects on the self-preservation behaviour of turbulent free jets. J. Fluid Mech. 254, 417–435.CrossRefGoogle Scholar
Ries, F., Obando, P., Shevchuck, I., Janicka, J. & Sadiki, A. 2017 Numerical analysis of turbulent flow dynamics and heat transport in a round jet at supercritical conditions. Intl J. Heat Fluid Flow 66, 172–184.Google Scholar
Roy, A., Joly, C. & Segal, C. 2013 Disintegrating supercritical jets in a subcritical environment. J. Fluid Mech. 717, 193–202.CrossRefGoogle Scholar
Schmitt, T., Selle, L., Ruiz, A. & Cuenot, B. 2010 Large-eddy simulation of supercritical-pressure round jets. AIAA J. 48 (9), 2133–2144.CrossRefGoogle Scholar
Sciacovelli, L. & Bellan, J. 2019 The influence of the chemical composition representation according to the number of species during mixing in high-pressure turbulent flows. J. Fluid Mech. 863, 293–340.CrossRefGoogle Scholar
Segal, C. & Polikhov, S.A. 2008 Subcritical to supercritical mixing. Phys. Fluids 20 (5), 052101.CrossRefGoogle Scholar
Selle, L. & Schmitt, T. 2010 Large-eddy simulation of single-species flows under supercritical thermodynamic conditions. Combust. Sci. Technol. 182 (4–6), 392–404.CrossRefGoogle Scholar
Sharan, N. 2016 Time-stable high-order finite difference methods for overset grids. PhD thesis, University of Illinois at Urbana-Champaign.Google Scholar
Sharan, N. & Bellan, J.R. 2019 Numerical aspects for physically accurate direct numerical simulations of turbulent jets. AIAA Paper 2019-2011.CrossRefGoogle Scholar
Sharan, N. & Bellan, J.R. 2021 Direct numerical simulation of high-pressure free jets. AIAA Paper 2021-0550.CrossRefGoogle Scholar
Sharan, N., Matheou, G. & Dimotakis, P.E. 2018 a Mixing, scalar boundedness, and numerical dissipation in large-eddy simulations. J. Comput. Phys. 369, 148–172.CrossRefGoogle Scholar
Sharan, N., Matheou, G. & Dimotakis, P.E. 2019 Turbulent shear-layer mixing: initial conditions, and direct-numerical and large-eddy simulations. J. Fluid Mech. 877, 35–81.CrossRefGoogle Scholar
Sharan, N., Pantano, C. & Bodony, D.J. 2018 b Time-stable overset grid method for hyperbolic problems using summation-by-parts operators. J. Comput. Phys. 361, 199–230.CrossRefGoogle Scholar
Simeoni, G.G., Bryk, T., Gorelli, F.A., Krisch, M., Ruocco, G., Santoro, M. & Scopigno, T. 2010 The widom line as the crossover between liquid-like and gas-like behaviour in supercritical fluids. Nat. Phys. 6 (7), 503–507.CrossRefGoogle Scholar
Simone, A., Coleman, G.N. & Cambon, C. 1997 The effect of compressibility on turbulent shear flow: a rapid-distortion-theory and direct-numerical-simulation study. J. Fluid Mech. 330, 307–338.CrossRefGoogle Scholar
Slessor, M.D., Bond, C.L. & Dimotakis, P.E. 1998 Turbulent shear-layer mixing at high Reynolds numbers: effects of inflow conditions. J. Fluid Mech. 376, 115–138.CrossRefGoogle Scholar
Taşkinoğlu, E.S. & Bellan, J. 2010 A posteriori study using a DNS database describing fluid disintegration and binary-species mixing under supercritical pressure: heptane and nitrogen. J. Fluid Mech. 645, 211–254.CrossRefGoogle Scholar
Taşkinoğlu, E.S. & Bellan, J. 2011 Subgrid-scale models and large-eddy simulation of oxygen stream disintegration and mixing with a hydrogen or helium stream at supercritical pressure. J. Fluid Mech. 679, 156–193.CrossRefGoogle Scholar
Townsend, A. 1980 The Structure of Turbulent Shear Flow. Cambridge University Press.Google Scholar
Vreman, A.W., Sandham, N.D. & Luo, K.H. 1996 Compressible mixing layer growth rate and turbulence characteristics. J. Fluid Mech. 320, 235–258.CrossRefGoogle Scholar
Woodward, R. & Talley, D. 1996 Raman imaging of transcritical cryogenic propellants. AIAA Paper 1996-468.CrossRefGoogle Scholar
Wygnanski, I., Champagne, F. & Marasli, B. 1986 On the large-scale structures in two-dimensional, small-deficit, turbulent wakes. J. Fluid Mech. 168, 31–71.CrossRefGoogle Scholar
Wygnanski, I. & Fiedler, H.O. 1969 Some measurements in the self-preserving jet. J. Fluid Mech. 38 (3), 577–612.CrossRefGoogle Scholar
Xu, G. & Antonia, R. 2002 Effect of different initial conditions on a turbulent round free jet. Exp. Fluids 33 (5), 677–683.CrossRefGoogle Scholar