Hostname: page-component-586b7cd67f-t8hqh Total loading time: 0 Render date: 2024-11-22T15:13:56.343Z Has data issue: false hasContentIssue false
  • English
  • Français

Investigation of Boussinesq dynamics using intermediate models based on wave–vortical interactions

Published online by Cambridge University Press:  15 April 2014

Gerardo Hernandez-Duenas ,
Leslie M. Smith  and
Samuel N. Stechmann
Gerardo Hernandez-Duenas*
Affiliation:
Department of Mathematics, University of Wisconsin–Madison, Madison, WI 53706, USA
Leslie M. Smith
Affiliation:
Department of Mathematics, University of Wisconsin–Madison, Madison, WI 53706, USA Department of Engineering Physics, University of Wisconsin–Madison, Madison, WI 53706, USA
Samuel N. Stechmann
Affiliation:
Department of Mathematics, University of Wisconsin–Madison, Madison, WI 53706, USA Department of Atmospheric and Oceanic Sciences, University of Wisconsin–Madison, Madison, WI 53706, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Nonlinear coupling among wave modes and vortical modes is investigated with the following question in mind: can we distinguish the wave–vortical interactions largely responsible for formation versus evolution of coherent, balanced structures? The two main case studies use initial conditions that project only onto the vortical-mode flow component of the rotating Boussinesq equations: (i) an initially balanced dipole and (ii) random initial data in the vortical modes. Both case studies compare quasi-geostrophic (QG) dynamics (involving only nonlinear interactions between vortical modes) to the dynamics of intermediate models allowing for two-way feedback between wave modes and vortical modes. For an initially balanced dipole with symmetry across the 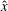$\hat{\boldsymbol {x}}$-axis, the QG dipole will propagate along the 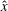$\hat{\boldsymbol {x}}$-axis while the trajectory of the Boussinesq dipole exhibits a cyclonic drift. Compared to a forced linear (FL) model with one-way forcing of wave modes by the vortical modes, the simplest intermediate model with two-way feedback involving vortical–vortical–wave interactions is able to capture the speed and trajectory of the dipole for roughly ten times longer at Rossby 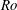$Ro$ and Froude 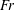$Fr$ numbers 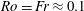$Ro = Fr \approx 0.1$. Despite its success at tracking the dipole, the latter intermediate model does not accurately capture the details of the flow structure within the adjusted dipole. For decay from random initial conditions in the vortical modes, the full Boussinesq equations generate vortices that are smaller than QG vortices, indicating that wave–vortical interactions are fundamental for creating the correct balanced state. The intermediate model with QG and vortical–vortical–wave interactions actually prevents the formation of vortices. Taken together these case studies suggest that: vortical–vortical–wave interactions create waves and thereby influence the evolution of balanced structures; vortical–wave–wave interactions take energy out of the wave modes and contribute in an essential way to the formation of coherent balanced structures.

JFM classification

Geophysical and Geological Flows: Rotating flows Geophysical and Geological Flows: Stratified flows
Type
Papers
Information
Journal of Fluid Mechanics , Volume 747 , 25 May 2014 , pp. 247 - 287
Copyright
© 2014 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Allen, J. S. 1993 Iterated geostrophic intermediate models. J. Phys. Oceanogr. 23, 2447–2461.Google Scholar
Babin, A., Mahalov, A. & Nicolaenko, B. 2000 Global regularity of 3D rotating Navier–Stokes equations for resonant domains. Appl. Maths Comput. 13 (4), 51–57.Google Scholar
Bartello, P. 1995 Geostrophic adjustment and inverse cascades in rotating stratified turbulence. J. Atmos. Sci. 52, 4410–4428.Google Scholar
Bourouiba, L. & Bartello, P. 2007 The intermediate Rossby number range and two-dimensional–three-dimensional transfers in rotating decaying homogeneous turbulence. J. Fluid Mech. 597, 139–161.Google Scholar
Boyd, J. P. 2001 Chebyshev and Fourier Special Methods. Dover.Google Scholar
Caillol, P. & Zeitlin, V. 2000 Kinetic equations and stationary energy spectra of weakly nonlinear internal gravity waves. Dyn. Atmos. Oceans 32 (2), 81–112.Google Scholar
Cambon, C., Mansour, N. N. & Godeferd, F. S. 1997 Energy transfer in rotating turbulence. J. Fluid Mech. 337, 303–332.Google Scholar
Cambon, C., Rubinstein, R. & Godeferd, F. S. 2004 Advances in wave turbulence: rapidly rotating flows. New J. Phys. 6 (1), 73.Google Scholar
Canuto, C., Hussaini, M. Y., Quarteroni, A. & Zhang, T. A. 2006 Spectral Methods: Fundamentals in Single Domains. Springer.Google Scholar
Charney, J. G. 1948 On the scale of atmospheric motions. Geofys. Publ. Norske Vid.-Akad. Oslo 17 (2), 251–261.Google Scholar
Cunningham, P. & Keyser, D. 2004 Dynamics of jet streaks in a stratified quasi-geostrophic atmosphere: steady-state representations. Q. J. R. Meteorol. Soc. 130 (600), 1579–1609.Google Scholar
Deusebio, E., Vallgren, A. & Lindborg, E. 2013 The route to dissipation in strongly stratified and rotating flows. J. Fluid Mech. 720, 66–103.Google Scholar
Embid, P. F. & Majda, A. J. 1998 Low Froude number limiting dynamics for stably stratified flow with small or finite Rossby numbers. Geophys. Astrophys. Fluid Dyn. 87 (1–2), 1–50.Google Scholar
Flierl, G. R. 1987 Isolated eddy models in geophysics. Annu. Rev. Fluid Mech. 19, 493–530.CrossRefGoogle Scholar
Ford, R., McIntyre, M. E. & Norton, W. A. 2000 Balance and the slow quasi manifold: some explicit results. J. Atmos. Sci. 57, 1236–1254.2.0.CO;2>CrossRefGoogle Scholar
Fritts, D. C. & Alexander, M. J. 2003 Gravity wave dynamics and effects in the middle atmosphere. Rev. Geophys. 41 (1), 1003.Google Scholar
Galtier, S. 2003 Weak inertial-wave turbulence theory. Phys. Rev. E 68 (1), 015301.Google Scholar
Gill, A. E. 1982 Atmosphere-Ocean Dynamics. Academic.Google Scholar
Greenspan, H. P. 1968 The Theory of Rotating Fluids. Cambridge University Press.Google Scholar
Hakim, G. J., Snyder, C. & Muraki, D. J. 2002 A new surface model for cyclone-anticyclone asymmetry. J. Atmos. Sci. 59, 2405–2420.Google Scholar
Hasselmann, K. 1962 On the nonlinear energy transfer in a gravity-wave spectrum. Part 1. General theory. J. Fluid Mech. 12 (4), 481–500.Google Scholar
Hopfinger, E. J., Browand, F. K. & Gagne, Y. 1982 Turbulence and waves in a rotating tank. J. Fluid Mech. 125, 505–534.Google Scholar
Kizner, Z., Reznik, G., Fridman, B., Khvoles, R. & McWilliams, J. 2008 Shallow water modons on the $f$ -plane. J. Fluid Mech. 603, 305–329.Google Scholar
Kraichnan, R. H. 1973 Helical turbulence and absolute equilibrium. J. Fluid Mech. 59, 745–752.Google Scholar
Kuo, A. C. & Polvani, L. M. 2000 Nonlinear geostrophic adjustment, cyclone/anticyclone asymmetry, and potential vorticity rearrangement. Phys. Fluids 12 (5), 1087–1100.Google Scholar
Laval, J. P., McWilliams, J. C. & Dubrulle, B. 2003 Forced stratified turbulence: successive transitions with Reynolds number. Phys. Rev. E 68, 36308.CrossRefGoogle ScholarPubMed
Ledwell, J. R., Montgomery, E. T., Polzin, K. L., Laurent, L. C. St., Schmitt, R. W. & Toole, J. M. 2000 Evidence for enhanced mixing over rough topography in the abyssal ocean. Nature 403 (6766), 179–182.Google Scholar
Lee, Y. & Smith, L. M. 2007 On the formation of geophysical and planetary zonal flows by near-resonant wave interactions. J. Fluid Mech. 576, 405–424.Google Scholar
Lelong, M.-P. & Riley, J. J. 1991 Internal wave–vortical mode interactions in strongly stratified flows. J. Fluid Mech. 232, 1–19.Google Scholar
Lorenz, E. N. & Krishnamurthy, V. 1987 On the nonexistence of a slow manifold. J. Atmos. Sci. 44, 2940–2950.Google Scholar
Lvov, Y. V., Polzin, K. L. & Tabak, E. G. 2004 Energy spectra of the ocean’s internal wavefield: theory and observations. Phys. Rev. Lett. 92 (12), 128501.Google Scholar
Lvov, Y. V., Polzin, K. L. & Yokoyama, N. 2012 Resonant and near-resonant internal wave interactions. J. Phys. Oceanogr. 42 (5), 669–691.Google Scholar
Majda, A. 2003 Introduction to PDEs and Waves for the Atmosphere and Ocean.. (Courant Lecture Notes in Mathematics) , vol. 9. New York University Courant Institute of Mathematical Sciences.Google Scholar
McComas, C. H. & Bretherton, F. P. 1977 Resonant interaction of oceanic internal waves. J. Geophys. Res. 82 (9), 1397–1412.Google Scholar
McIntyre, M. E. 2009 Spontaneous imbalance and hybrid vortex-gravity structures. J. Atmos. Sci. 66 (5), 1315–1326.Google Scholar
McIntyre, M. E. & Norton, W. A. 2000 Potential vorticity inversion on a hemisphere. J. Atmos. Sci. 57 (9), 1214–1235.2.0.CO;2>CrossRefGoogle Scholar
McWilliams, J. C. & Gent, P. R. 1980 Intermediate models of planetary circulations in the atmosphere and ocean. J. Atmos. Sci. 37, 1657–1678.Google Scholar
Metais, O., Bartello, P., Garnier, E., Riley, J. J. & Lesieur, M. 1996 Inverse cascade in stably stratified rotating turbulence. Dyn. Atmos. Oceans 23 (1), 193–203.Google Scholar
Mohebalhojeh, A. R. & Dritschel, D. G. 2001 Hierarchies of balance conditions for the $f$ -plane shallow-water equations. J. Atmos. Sci. 58 (16), 2411–2426.Google Scholar
Muraki, D. J. & Hakim, G. J. 2001 Balanced asymmetries of waves on the tropopause. J. Atmos. Sci. 58 (3), 237–252.Google Scholar
Muraki, D. J., Snyder, C. & Rotunno, R. 1999 The next-order corrections to quasigeostrophic theory. J. Atmos. Sci. 56 (11), 1547–1560.Google Scholar
Newell, A. C. 1969 Rossby wavepacket interactions. J. Fluid Mech. 35 (2), 255–271.CrossRefGoogle Scholar
O’Sullivan, D. & Dunkerton, T. J. 1995 Generation of inertia-gravity waves in a simulated life cycle of baroclinic instability. J. Atmos. Sci. 52, 3695–3716.Google Scholar
Pedlosky, J. 1982 Geophysical Fluid Dynamics. Springer.Google Scholar
Plougonven, R. & Zeitlin, V. 2002 Internal gravity wave emission from a pancake vortex: an example of wave–vortex interaction in strongly stratified flows. Phys. Fluids 14 (3), 1259–1268.Google Scholar
Polvani, L. M., McWilliams, J. C., Spall, M. A. & Ford, R. 1994 The coherent structures of shallow-water turbulence: deformation-radius effects, cyclone/anticyclone asymmetry and gravity-wave generation. Chaos 4 (2), 177–186.Google Scholar
Praud, O., Sommeria, J. & Fincham, A. M. 2007 Decaying grid turbulence in a rotating stratified fluid. J. Fluid Mech. 547, 389–412.Google Scholar
Remmel, M.2010 New models for the rotating shallow water and Boussinesq equations by subsets of mode interactions. ProQuest LLC, Ann Arbor, MI; PhD thesis, The University of Wisconsin–Madison.Google Scholar
Remmel, M. & Smith, L. M. 2009 New intermediate models for rotating shallow water and an investigation of the preference for anticyclones. J. Fluid Mech. 635, 321–359.Google Scholar
Remmel, M., Sukhatme, J. & Smith, L. M. 2010 Nonlinear inertia-gravity wave-mode interactions in three dimensional rotating stratified flows. Commun. Math. Sci. 8 (2), 357–376.Google Scholar
Remmel, M., Sukhatme, J. & Smith, L. 2014 Nonlinear gravity-wave interactions in stratified turbulence. Theor. Comp. Fluid. Dyn. 28 (2), 131–145.Google Scholar
Ribstein, B., Gula, J. & Zeitlin, V. 2010 (A)geostrophic adjustment of dipolar perturbations, formation of coherent structures and their properties, as follows from high-resolution numerical simulations with rotating shallow water model. Phys. Fluids 22, 116603.CrossRefGoogle Scholar
Salmon, R. 1998 Lectures on Geophysical Fluid Dynamics. Oxford University Press.Google Scholar
Smith, L. M. & Lee, Y. 2005 On near resonances and symmetry breaking in forced rotating flows at moderate Rossby number. J. Fluid Mech. 535, 111–142.Google Scholar
Smith, L. M. & Waleffe, F. 1999 Transfer of energy to two-dimensional large scales in forced, rotating three-dimensional turbulence. Phys. Fluids 11 (6), 1608–1622.Google Scholar
Smith, L. M. & Waleffe, F. 2002 Generation of slow large scales in forced rotating stratified turbulence. J. Fluid Mech. 451, 145–168.Google Scholar
Snyder, C. 1999 Error growth in flows with finite-amplitude waves or coherent structures. J. Atmos. Sci. 56, 500–506.Google Scholar
Snyder, C., Muraki, D. J., Plougonven, R. & Zhang, F. 2007 Inertia-gravity waves generated within a dipole vortex. J. Atmos. Sci. 64 (12), 4417–4431.Google Scholar
Snyder, C., Plougonven, R. & Muraki, D. J. 2009 Mechanisms for spontaneous gravity wave generation within a dipole vortex. J. Atmos. Sci. 66 (11), 3464–3478.Google Scholar
Spiegel, E. A. & Veronis, G. 1960 On the Boussinesq approximation for a compressible fluid. Astrophys. J. 131, 442–447.Google Scholar
Vallis, G. K. 1996 Potential vorticity inversion and balanced equations of motion for rotating and stratified flows. Q. J. R. Meteorol. Soc. 122 (529), 291–322.Google Scholar
Vallis, G. K. 2006 Atmospheric and Oceanic Fluid Dynamics: Fundamentals and Large-Scale Circulation. Cambridge University Press.Google Scholar
Vanneste, J. 2013 Balance and spontaneous wave generation in geophysical flows. Annu. Rev. Fluid Mech. 45, 147–172.Google Scholar
Vanneste, J. & Yavneh, I. 2004 Exponentially small inertia-gravity waves and the breakdown of quasigeostrophic balance. J. Atmos. Sci. 61, 211–223.Google Scholar
Viúdez, Á. 2007 The origin of the stationary frontal wavepacket spontaneously generated in rotating stratified vortex dipoles. J. Fluid Mech. 593, 359–383.CrossRefGoogle Scholar
Waite, M. L. & Bartello, P. 2006 The transition from geostrophic to stratified turbulence. J. Fluid Mech. 568, 89–108.Google Scholar
Waleffe, F. 1993 Inertial transfers in the helical decomposition. Phys. Fluids A 5, 677–685.Google Scholar
Wang, S. & Zhang, F. 2010 Source of gravity waves within a vortex-dipole jet revealed by a linear model. J. Atmos. Sci. 67 (5), 1438–1455.Google Scholar
Wang, S., Zhang, F. & Epifanio, C. C. 2010 Forced gravity wave response near the jet exit region in a linear model. Q. J. R. Meteorol. Soc. 136, 1773–1787.Google Scholar
Wang, S., Zhang, F. & Snyder, C. 2009 Generation and propagation of inertia-gravity waves from vortex dipoles and jets. J. Atmos. Sci. 66 (5), 1294–1314.Google Scholar
Warn, T., Bokhove, O., Shepherd, T. G. & Vallis, G. K. 1995 Rossby number expansions, slaving principles, and balance dynamics. Q. J. R. Meteorol. Soc. 121 (523), 723–739.CrossRefGoogle Scholar
Warner, C. D. & McIntyre, M. E. 2001 An ultrasimple spectral parameterization for nonorographic gravity waves. J. Atmos. Sci. 58 (14), 1837–1857.Google Scholar
Wunsch, C. & Ferrari, R. 2004 Vertical mixing, energy, and the general circulation of the oceans. Annu. Rev. Fluid Mech. 36, 281–314.Google Scholar
Zakharov, V. E., Lvov, V. S. & Falkovich, G. 1992 Kolmogorov Spectra of Turbulence 1. Wave Turbulence. Springer.CrossRefGoogle Scholar
Zeitlin, V. 2008 Decoupling of balanced and unbalanced motions and inertia-gravity wave emission: small versus large rossby numbers. J. Atmos. Sci. 65 (11), 3528–3542.Google Scholar