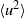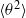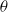The paper examines the validity of velocity and scalar invariants in slightly heated and approximately isotropic turbulence generated by passive conventional grids. By assuming that the variances $\langle {u}^{2} \rangle $ and $\langle {\theta }^{2} \rangle $ ($u$ and $\theta $ represent the longitudinal velocity and temperature fluctuations) decay along the streamwise direction $x$ according to power laws 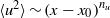$\langle {u}^{2} \rangle \sim {(x- {x}_{0} )}^{{n}_{u} } $ and 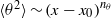$\langle {\theta }^{2} \rangle \sim {(x- {x}_{0} )}^{{n}_{\theta } } $ (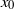${x}_{0} $ is the virtual origin of the flow) and with the further assumption that the one-point energy and scalar variance budgets are represented closely by a balance between the rates of change of 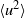$\langle {u}^{2} \rangle $ and 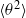$\langle {\theta }^{2} \rangle $ and the corresponding mean energy dissipation rates, the products 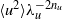$\langle {u}^{2} \rangle { \lambda }_{u}^{- 2{n}_{u} } $ and 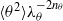$\langle {\theta }^{2} \rangle { \lambda }_{\theta }^{- 2{n}_{\theta } } $ must remain constant with respect to $x$. Here 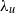${\lambda }_{u} $ and 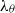${\lambda }_{\theta } $ are the Taylor and Corrsin microscales. 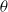This is unambiguously supported by previously available data, as well as new measurements of $u$ and $\theta $ made at small Reynolds numbers downstream of three different biplane grids. 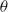Implications for invariants based on measured integral length scales of $u$ and $\theta $ are also tested after confirming that the dimensionless energy and scalar variance dissipation rate parameters are approximately constant with $x$. Since the magnitudes of 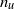${n}_{u} $ and 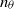${n}_{\theta } $ vary from grid to grid and may also depend on the Reynolds number, the Saffman and Corrsin invariants which correspond to a value of 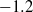$- 1. 2$ for 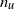${n}_{u} $ and 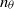${n}_{\theta } $ are unlikely to apply in general. The effect of the Reynolds number on 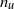${n}_{u} $ is discussed in the context of published data for both passive and active grids.