Hostname: page-component-78c5997874-ndw9j Total loading time: 0 Render date: 2024-11-17T13:18:50.971Z Has data issue: false hasContentIssue false
  • English
  • Français

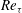Invariant solutions of minimal large-scale structures in turbulent channel flow for $Re_{\unicode[STIX]{x1D70F}}$ up to 1000

Published online by Cambridge University Press:  01 August 2016

Yongyun Hwang ,
Ashley P. Willis  and
Carlo Cossu Open the ORCID record for Carlo Cossu [Opens in a new window]
Yongyun Hwang*
Affiliation:
Department of Aeronautics, Imperial College London, South Kensington, London SW7 2AZ, UK
Ashley P. Willis
Affiliation:
School of Mathematics and Statistics, University of Sheffield, Sheffield S3 7RH, UK
Carlo Cossu
Affiliation:
Institut de Mécanique des Fluides de Toulouse (IMFT), CNRS Université de Toulouse, Allée du Pr. Camille Soula, F-31400 Toulouse, France
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

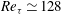Understanding the origin of large-scale structures in high-Reynolds-number wall turbulence has been a central issue over a number of years. Recently, Rawat et al. (J. Fluid Mech., vol. 782, 2015, pp. 515–540) have computed invariant solutions for the large-scale structures in turbulent Couette flow at $Re_{\unicode[STIX]{x1D70F}}\simeq 128$ using an overdamped large-eddy simulation with the Smagorinsky model to account for the effect of the surrounding small-scale motions. Here, we extend this approach to Reynolds numbers an order of magnitude higher in turbulent channel flow, towards the regime where the large-scale structures in the form of very-large-scale motions (long streaky motions) and large-scale motions (short vortical structures) emerge energetically. We demonstrate that a set of invariant solutions can be computed from simulations of the self-sustaining large-scale structures in the minimal unit (domain of size 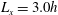$L_{x}=3.0h$ streamwise and 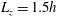$L_{z}=1.5h$ spanwise) with midplane reflection symmetry at least up to 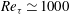$Re_{\unicode[STIX]{x1D70F}}\simeq 1000$. By approximating the surrounding small scales with an artificially elevated Smagorinsky constant, a set of equilibrium states are found, labelled upper- and lower-branch according to their associated drag. It is shown that the upper-branch equilibrium state is a reasonable proxy for the spatial structure and the turbulent statistics of the self-sustaining large-scale structures.

JFM classification

Nonlinear Dynamical Systems: Low-dimensional models Nonlinear Dynamical Systems: Nonlinear Dynamical Systems Turbulent Flows: Turbulent boundary layers
Type
Rapids
Information
Journal of Fluid Mechanics , Volume 802 , 10 September 2016 , R1
Check for updates
Copyright
© 2016 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Adrian, R. J. 2007 Hairpin vortex organization in wall turbulence. Phys. Fluids 19, 041301.CrossRefGoogle Scholar
del Álamo, J. C. & Jiménez, J. 2009 Estimation of turbulent convection velocities and corrections to Taylor’s approximation. J. Fluid Mech. 640, 5–26.Google Scholar
del Álamo, J. C., Jiménez, J., Zandonade, P. & Moser, R. D. 2004 Scaling of the energy spectra of turbulent channels. J. Fluid Mech. 500, 135–144.Google Scholar
Avila, M., Mellibovsky, F., Roland, N. & Hof, B. 2013 Streamwise-localized solutions at the onset of turbulence in pipe flow. Phys. Rev. Lett. 110, 224502.CrossRefGoogle ScholarPubMed
Bewley, T. R. 2014 Numerical Renaissance: Simulation, Optimization, and Control. Renaissance Press.Google Scholar
Cossu, C., Pujals, G. & Depardon, S. 2009 Optimal transient growth and very large scale structures in turbulent boundary layers. J. Fluid Mech. 619, 79–94.Google Scholar
Duguet, Y., Willis, A. P. & Kerswell, R. R. 2008 Transition in pipe flow: the saddle structure on the boundary of turbulence. J. Fluid Mech. 613, 255–274.CrossRefGoogle Scholar
Faisst, H. & Eckhardt, B. 2003 Travelling waves in pipe flow. Phys. Rev. Lett. 91, 224502.CrossRefGoogle ScholarPubMed
Flores, O. & Jiménez, J. 2010 Hierarchy of minimal flow units in the logarithmic layer. Phys. Fluids 22, 071704.Google Scholar
Flores, O., Jiménez, J. & del Álamo, J. C. 2007 Vorticity organization in the outer layer of turbulent channels with disturbed walls. J. Fluid Mech. 591, 145–154.Google Scholar
Gibson, J. F., Halcrow, J. & Cvitanovic, P. 2008 Visualizing the geometry of state space in plane Couette flow. J. Fluid Mech. 611, 107–130.Google Scholar
Hall, P. & Sherwin, S. J. 2010 Streamwise vortices in shear flows: harbingers of transition and the skeleton of coherent structures. J. Fluid Mech. 661, 178–205.CrossRefGoogle Scholar
Härtel, C. & Kleiser, L. 1998 Analysis and modelling of subgrid-scale motions in near-wall turbulence. J. Fluid Mech. 356, 327–352.Google Scholar
Hutchins, N. & Marusic, I. 2007 Evidence of very long meandering features in the logarithmic region of turbulent boundary layers. J. Fluid Mech. 579, 1–28.CrossRefGoogle Scholar
Hwang, Y. 2015 Statistical structure of self-sustaining attached eddies in turbulent channel flow. J. Fluid Mech. 723, 264–288.CrossRefGoogle Scholar
Hwang, Y. & Bengana, Y. 2016 Self-sustaining process of minimal attached eddies in turbulent channel flow. J. Fluid Mech. 795, 708–738.Google Scholar
Hwang, Y. & Cossu, C. 2010a Linear non-normal energy amplification of harmonic and stochastic forcing in the turbulent channel flow. J. Fluid Mech. 664, 51–73.Google Scholar
Hwang, Y. & Cossu, C. 2010b Self-sustained process at large scales in turbulent channel flow. Phys. Rev. Lett. 105, 044505.Google Scholar
Hwang, Y. & Cossu, C. 2011 Self-sustained processes in the logarithmic layer of turbulent channel flows. Phys. Fluids 23, 061702.CrossRefGoogle Scholar
Kawahara, G. & Kida, S. 2001 Periodic motion embedded in plane Couette turbulence: regeneration cycle and burst. J. Fluid Mech. 449, 291–300.Google Scholar
Kerswell, R. R. & Tutty, O. R. 2007 Recurrence of travelling waves in transitional pipe flow. J. Fluid Mech. 584, 69–102.Google Scholar
Kovasznay, L. S. G., Kibens, V. & Blackwelder, R. F. 1970 Large-scale motion in the intermittent region of a turbulent boundary layer. J. Fluid Mech. 41, 283–325.CrossRefGoogle Scholar
Mason, P. J. & Cullen, N. J. 1986 On the magnitude of the subgrid-scale eddy coefficient in large-eddy simulations of turbulent channel flow. J. Fluid Mech. 162, 439–462.CrossRefGoogle Scholar
Meneveau, C. & Katz, J. 2000 Scale-invariance and turbulence models for large-eddy simulation. Annu. Rev. Fluid. Mech. 32, 1–32.Google Scholar
Moin, P. & Kim, J. 1982 Numerical investigation of turbulent channel flow. J. Fluid Mech. 118, 341–377.CrossRefGoogle Scholar
Nagata, M. 1990 Three-dimensional finite-amplitude solutions in plane Couette flow: bifurcation from infinity. J. Fluid Mech. 217, 519–527.Google Scholar
Park, J., Hwang, Y. & Cossu, C. 2011 On the stability of large-scale streaks in the turbulent Couette and Poiseuille flows. C. R. Mèc. 339 (1), 1–5.CrossRefGoogle Scholar
Park, J. S. & Graham, M. D. 2016 Exact coherent states and connections to turbulent dynamics in minimal channel flow. J. Fluid Mech. 782, 430–454.Google Scholar
Perry, A. E. & Chong, M. S. 1982 On the mechanism of turbulence. J. Fluid Mech. 119, 173–217.CrossRefGoogle Scholar
Pujals, G., García-Villalba, M., Cossu, C. & Depardon, S. 2009 A note on optimal transient growth in turbulent channel flows. Phys. Fluids 21, 015109.CrossRefGoogle Scholar
Rawat, S.2014 Coherent dynamics of large-scale turbulent motions. PhD thesis, Université de Toulouse, http://ethesis.inp-toulouse.fr/archive/00003011.Google Scholar
Rawat, S., Cossu, C., Hwang, Y. & Rincon, F. 2015 On the self-sustained nature of large-scale motions in turbulent Couette flow. J. Fluid Mech. 782, 515–540.Google Scholar
Rawat, S., Cossu, C. & Rincon, F. 2016 Travelling-wave solutions bifurcating from relative periodic orbits in plane Poiseuille flow. C. R. Méc. 344, 448–455.Google Scholar
Schneider, T. M., Eckhardt, B. & Yorke, J. A. 2007 Turbulence transition and the edge of chaos in pipe flow. Phys. Rev. Lett. 99, 034502.Google Scholar
Skufca, J. D., Yorke, J. A. & Eckhardt, B. 2006 Edge of chaos in a parallel shear flow. Phys. Rev. Lett. 96 (17), 174101.Google Scholar
Song, B., Barkley, D., Hof, B. & Avila, M.2016 Speed and structure of turbulent fronts in pipe flow. arXiv:1603.04077.Google Scholar
Townsend, A. A. 1976 The Structure of Turbulent Shear Flow. Cambridge University Press.Google Scholar
Viswanath, D. 2007 Recurrent motions within plane Couette turbulence. J. Fluid Mech. 580, 339–358.CrossRefGoogle Scholar
Waleffe, F. 2001 Exact coherent structures in channel flow. J. Fluid Mech. 435, 93–102.Google Scholar
Wedin, H. & Kerswell, R. R. 2004 Exact coherent structures in pipe flow: travelling wave solutions. J. Fluid Mech. 508, 333–371.Google Scholar
Willis, A. P., Cvitanovic, P. & Avila, M. 2013 Revealing the state space of turbulent pipe flow by symmetry reduction. J. Fluid Mech. 721, 514–540.Google Scholar
Willis, A. P., Cvitanovic, P. & Avila, M. 2016 Symmetry reduction in high dimensions, illustrated in a turbulent pipe. Phys. Rev. E 93, 022204.Google Scholar
Willis, A. P., Hwang, Y. & Cossu, C. 2010 Optimally amplified large-scale streaks and drag reduction in the turbulent pipe flow. Phys. Rev. E 82, 036321.Google Scholar
Zang, T. A. 1991 Numerical simulation of the dynamics of turbulent boundary layers: perspectives of a transition simulator. Phil. Trans. R. Soc. Lond. A 336, 95–102.Google Scholar