Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2024-12-27T02:54:51.508Z Has data issue: false hasContentIssue false
  • English
  • Français

The internal wavefield generated by a towed sphere at low Froude number

Published online by Cambridge University Press:  13 March 2015

A. Brandt  and
J. R. Rottier
A. Brandt*
Affiliation:
The Johns Hopkins University Applied Physics Laboratory, 11100 Johns Hopkins Road, Laurel, MD 20723-6099, USA
J. R. Rottier
Affiliation:
The Johns Hopkins University Applied Physics Laboratory, 11100 Johns Hopkins Road, Laurel, MD 20723-6099, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

In highly stratified atmospheric and oceanic environments, a large fraction of energy input by various sources can be manifest as internal waves (IWs). The propagating nature of IWs results in the distribution of the energy over a large fraction of the air/water column. Wakes of translating bodies are one source of input energy that has been of continued interest. To further the understanding of wakes in strongly stratified environments, and particularly the near-field regime where strong coupling to the internal wavefield is evident, an extensive series of experiments on the internal wavefield generated by a towed sphere was performed, wherein the internal wavefield was measured over a Froude number range 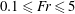$0.1\leqslant \mathit{Fr}\leqslant 5$ (where 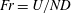$\mathit{Fr}=U/ND$, 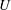$U$ is the tow speed, 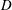$D$ the sphere diameter and 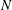$N$ the Brunt–Väisälä (BV) frequency). In a second series of experiments, the temporal wavefield evolution was studied over two BV periods. These measurements show that the body generation (lee wave) mechanism dominates at 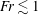$\mathit{Fr}\lesssim 1$, while the random eddies in the turbulent wake become the dominant source at 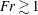$\mathit{Fr}\gtrsim 1$. In the low-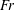$\mathit{Fr}$ regime, 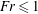$\mathit{Fr}\leqslant 1$, there is a resonant peak in the coupling of the input wake energy to the internal wavefield at a Froude number of 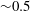${\sim}0.5$, and at its maximum 70 % of the input energy is coupled into IW potential energy. In this regime it was also found that the spreading angle of the evolving wavefield was considerably broader than predicted by the classical point-source models for the wavefield further downstream, owing to the existence in the near field of a significant energy content in the higher-IW modes that deteriorate at later times. In the low-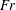$\mathit{Fr}$ regime, it was found that, while the IW potential energy increases 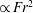$\propto \mathit{Fr}^{2}$, the fraction of the total energy input is a weak function of 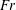$\mathit{Fr}$, varying as 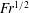$\mathit{Fr}^{1/2}$.

JFM classification

Geophysical and Geological Flows: Internal waves Turbulent Flows: Stratified turbulence Wakes/Jets: Wakes
Type
Papers
Information
Journal of Fluid Mechanics , Volume 769 , 25 April 2015 , pp. 103 - 129
Check for updates
Copyright
© 2015 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abdilghanie, A. M. & Diamessis, P. J. 2013 The internal gravity wave field emitted by a stably stratified turbulent wake. J. Fluid Mech. 720, 104–139.Google Scholar
Achenbach, E. 1974 The effects of surface roughness and tunnel blockage on the flow past spheres. J. Fluid Mech. 65, 113–125.Google Scholar
Baines, P. 1995 Topographic Effects in Stratified Flows. Cambridge University Press.Google Scholar
Bell, T. H. 1975 Lee waves in stratified flows with simple harmonic time dependence. J. Fluid Mech. 67, 705–722.CrossRefGoogle Scholar
Bonneton, P., Chomaz, J. M. & Hopfinger, E. J. 1993 Internal waves produced by the turbulent wake of a sphere moving horizontally in a stratified fluid. J. Fluid Mech. 254, 23–40.CrossRefGoogle Scholar
Bonneton, P., Chomaz, J. M., Hopfinger, E. J. & Perrier, M. 1996 The structure of the turbulent wake and the random internal wave field generated by a moving sphere in a stratified fluid. Dyn. Atmos. Oceans 23, 299–308.Google Scholar
Bonnier, M. & Eiff, O. 2002 On experimental investigation of the collapse of a turbulent wake in a stably stratified fluid. Phys. Fluids 14, 791–801.Google Scholar
Brandt, A.1999 Evolution of vortices generated by the collapse of a stratified, turbulent wake. In IUGG-99, XXII General Assembly, 19–30 July 1999, presentation, Birmingham, UK. IUGG.Google Scholar
Brandt, A. & Schemm, C. E.2011 Small-scale structure in the near field of a stratified wake. In Proceedings of the 7th International Symposium on Stratified Flows, Rome, Italy, 22–26 August 2011.Google Scholar
Brucker, K. A. & Sarkar, S. 2010 A comparative study of self-propelled and towed wakes in a stratified fluid. J. Fluid Mech. 652, 373–404.Google Scholar
Castro, I. P., Snyder, W. H. & Baines, P. G. 1990 Obstacle drag in stratified flow. Proc. R. Soc. Lond. A 429, 119–140.Google Scholar
Cerasoli, C. P. 1978 Experiments on buoyant-parcel motion and the generation of internal waves. J. Fluid Mech. 86, 247–271.Google Scholar
Chang, Y., Zhao, F., Zhang, J., Hong, F.-W., Li, P. & Yun, J. 2006 Numerical simulation of internal waves excited by a submarine moving in the two-layer stratified fluid. J. Hydrodyn. 18 (3), 330–336; Supplement 1.CrossRefGoogle Scholar
Chernyshenko, S. I. & Castro, I. P. 1996 High-Reynolds-number weakly stratified flow past an obstacle. J. Fluid Mech. 317, 155–178.Google Scholar
Chomaz, J. M., Bonneton, P., Butet, A. & Hopfinger, E. J. 1993a Vertical diffusion in the far wake of a sphere moving in a stratified fluid. Phys. Fluids A 5, 2799–2806.CrossRefGoogle Scholar
Chomaz, J. M., Bonneton, P., Butet, A., Hopfinger, E. J. & Perrier, M. 1991 Gravity wave patterns in the wake of a sphere in a stratified fluid. In Turbulence and Coherent Structures (ed. Metais, O. & Lesieur, M.), pp. 489–503. Kluwer Academic.CrossRefGoogle Scholar
Chomaz, J. M., Bonneton, P., Butet, A. & Perrier, M. 1992 Froude number dependence of the flow separation line on a sphere towed in a stratified fluid. Phys. Fluids A 2, 254–258.Google Scholar
Chomaz, J. M., Bonneton, P. & Hopfinger, E. J. 1993b The structure of the near wake of a sphere moving horizontally in a stratified fluid. J. Fluid Mech. 254, 1–21.Google Scholar
Dalziel, S. B., Patterson, M. D., Caulfied, C. P. & Le Brun, S. 2011 The structure of low-Froude-number lee waves over an isolated obstacle. J. Fluid Mech. 689, 3–31.Google Scholar
DeSilva, I. P. D. & Fernando, H. J. S. 1998 Experiments on collapsing turbulent regions in stratified fluids. J. Fluid Mech. 358, 29–60.CrossRefGoogle Scholar
Diamessis, P. J. & Abdilghanie, A. M.2011 The internal wave field radiated by a stably stratified turbulent wake. In Proceedings of the 7th International Symposium on Stratified Flows, Rome, Italy, 22–26 August 2011.Google Scholar
Diamessis, P. J., Gurka, R. & Liberzon, A. 2010 Spatial characterization of vortical structures and internal waves in a stratified turbulent wake using proper orthogonal decomposition. Phys. Fluids 22, 086601.Google Scholar
Diamessis, P. J., Spedding, G. R. & Domaradzki, J. A. 2011 Similarity scaling and vorticity structure in high-Reynolds-number stably stratified turbulent wakes. J. Fluid Mech. 671, 52–95.Google Scholar
Dohan, K. & Sutherland, B. R. 2005 Numerical and laboratory generation of internal waves from turbulence. Dyn. Atmos. Oceans 40, 43–56.CrossRefGoogle Scholar
Dupont, P., Kadri, Y. & Chomaz, J. M. 2001 Internal waves generated by the wake of Gaussian hills. Phys. Fluids 13, 3223–3233.Google Scholar
Dupont, P. & Voisin, B. 1996 Internal waves generated by a translating and oscillating sphere. Dyn. Atmos. Oceans 23, 289–298.CrossRefGoogle Scholar
Gilreath, H. E. & Brandt, A. 1985 Experiments on the generation of internal waves in a stratified fluid. AIAA J. 23, 693–700.CrossRefGoogle Scholar
Gorodtsov, V. A. & Teodorovich, E. V. 1982 Study of internal waves in the case of rapid horizontal motion of cylinders and spheres. Fluid Dyn. 17, 893–898; [Transl. from Izv. Akad. Nauk SSSR Mekh. Zhidk. Gaza 17 (6), 94–100].Google Scholar
Gourlay, M. J., Arendt, S. C., Fritts, D. C. & Werne, J. 2001 Numerical modeling of initially turbulent wakes with net momentum. Phys. Fluids 13 (12), 3783–3802.CrossRefGoogle Scholar
Greenslade, M. D. 2000 Drag on a sphere moving horizontally in a stratified fluid. J. Fluid Mech. 418, 339–350.Google Scholar
Hoerner, S. F. 1958 Fluid-Dynamic Drag. Published by the author.Google Scholar
Hopfinger, E. J., Flor, J.-B., Chomaz, J.-M. & Bonneton, P. 1991 Internal waves generated by a moving sphere and its wake in a stratified fluid. Exp. Fluids 11, 255–261.Google Scholar
Jacobitz, F. G., Rogers, M. M. & Ferziger, J. H. 2005 Waves in stably stratified turbulent flow. J. Turbul. 6 (N32), 1–12.Google Scholar
Keller, J. B. & Munk, W. H. 1970 Internal wave wakes of a body moving in a stratified fluid. Phys. Fluids 13, 1425–1431.Google Scholar
Lelong, M.-P. & Riley, J. J. 1991 Internal wave–vortical mode interactions in strongly stratified flows. J. Fluid Mech. 232, 1–19.Google Scholar
Lighthill, M. J. 1955 Waves in Fluids. Cambridge University Press.Google Scholar
Lighthill, M. J. 1996 Internal waves and related initial-value problems. Dyn. Atmos. Oceans 23, 3–17.Google Scholar
Lin, J.-T. & Pao, Y.-H. 1979 Wakes in stratified fluids. Annu. Rev. Fluid Mech. 11, 317–338.Google Scholar
Lin, Q., Boyer, D. L. & Fernando, H. J. S. 1992a Turbulent wakes of linearly stratified flow past a sphere. Phys. Fluids A 4, 1687–1696.Google Scholar
Lin, Q., Boyer, D. L. & Fernando, H. J. S. 1993 Internal waves generated by the turbulent wake of a sphere. Exp. Fluids 15, 147–154.Google Scholar
Lin, Q., Boyer, D. L. & Fernando, H. J. S. 1994 The vortex shedding of a streamwise-oscillating sphere translating through a linearly stratified fluid. Phys. Fluids A 6, 239–252.Google Scholar
Lin, Q., Lindberg, W. R., Boyer, D. L. & Fernando, H. J. S. 1992b Stratified flow past a sphere. J. Fluid Mech. 240, 315–354.Google Scholar
Lofquist, K. E. B. & Purtell, L. P. 1984 Drag on a sphere moving horizontally through a stratified liquid. J. Fluid Mech. 148, 271–284.Google Scholar
Long, R. R. 1972 Finite amplitude disturbances in the flow of inviscid rotating and stratified fluids over obstacles. Annu. Rev. Fluid Mech. 4, 69–92.Google Scholar
Meng, J. C. S. & Rottman, J. W. 1987 Linear internal waves generated by density and velocity perturbations in a linearly stratified fluid. J. Fluid Mech. 186, 419–444.Google Scholar
Mowbray, D. E. & Rarity, B. S. H. 1967 A theoretical and experimental investigation of the phase configuration of internal waves of small amplitude in a density stratified liquid. J. Fluid Mech. 28, 1–16.CrossRefGoogle Scholar
Riley, J. J., Lelong, M. P. G. & Slinn, D. N. 1991 Organized structures in strongly stratified flows. In Turbulence and Coherent Structures (ed. Metais, O. & Lesieur, M.), pp. 413–428. Kluwer Academic.CrossRefGoogle Scholar
Robey, H. F. 1997 The generation of internal waves by a towed sphere and its wake in a thermocline. Phys. Fluids A 9, 3353–3367.CrossRefGoogle Scholar
Rottman, J. W., Broutman, D., Spedding, G. & Diamessis, P.2006 A model for the internal wavefield produced by a submarine and its wake in the littoral ocean. In Proceedings of the 26th Symposium on Naval Hydrodynamics, 17–22 September 2006, Rome, Italy.Google Scholar
Scase, M. M. & Dalziel, S. B. 2004 Internal wave fields and drag generated by a translating body in a stratified fluid. J. Fluid Mech. 498, 289–313.CrossRefGoogle Scholar
Scase, M. M. & Dalziel, S. B. 2006 Internal wave fields generated by a translating body in a stratified fluid: an experimental comparison. J. Fluid Mech. 564, 305–331.Google Scholar
Schlichting, H. 1968 Boundary-Layer Theory, 6th edn. McGraw-Hill.Google Scholar
Sharman, R. D. & Wurtele, M. D. 1983 Ship waves and lee waves. J. Atmos. Sci. 40, 396–427.Google Scholar
Spedding, G. R. 1997 The evolution of initially-turbulent bluff-body wakes at high internal Froude number. J. Fluid Mech. 337, 283–301.Google Scholar
Spedding, G. R. 2014 Wake signature detection. Annu. Rev. Fluid Mech. 46, 273–302.CrossRefGoogle Scholar
Spedding, G. R., Browand, G. K. & Fincham, A. M. 1996a The long-time evolution of the initially turbulent wake of a sphere in a stable stratification. Dyn. Atmos. Oceans 23, 172–182.Google Scholar
Spedding, G. R., Browand, G. K. & Fincham, A. M. 1996b Turbulence, similarity scaling and vortex geometry in the wake of a towed sphere in a stably stratified fluid. J. Fluid Mech. 314, 53–103.Google Scholar
Sturova, I. V. 1978 Internal waves generated by local disturbances in a linearly stratified liquid of finite depth. J. Appl. Mech. Tech. Phys. 19 (3), 330–336.Google Scholar
Sturova, I. V. 1980 Internal waves generated in an exponentially stratified fluid by an arbitrarily moving source. Fluid Dyn. 15 (3), 378–383.Google Scholar
Van Dyke, M. 1982 An Album of Fluid Motion. Parabolic.Google Scholar
Vasholz, D. P. 2002 Low Froude number potential energy resonances in uniform stratification. Phys. Fluids 14, 458–461.Google Scholar
Vasholz, D. P. 2011 Stratified wakes, the high Froude number approximation, and potential flow. Theor. Comput. Fluid Dyn. 25, 357–379.Google Scholar
Vasil’ev, O. F., Voropaeva, O. F. & Kurbatskii, A. F. 2011 Turbulent mixing in stably stratified flows of the environment: the current state of the problem. Izv. Atmos. Ocean. Phys. 47 (3), 265–280.CrossRefGoogle Scholar
Voisin, B. 1994 Internal wave generation in uniformly stratified fluids. Part 2. Moving point sources. J. Fluid Mech. 261, 333–374.CrossRefGoogle Scholar
Voisin, B. 1995 Internal wave generation by turbulent wakes. In Mixing in Geophysical Flows (ed. Metais, O. & Lesieur, M.), pp. 291–301. CIMME.Google Scholar
Voisin, B. 2007 Lee waves from a sphere in a stratified flow. J. Fluid Mech. 574, 273–315.Google Scholar
Vosper, S. B., Castro, I. P., Snyder, W. H. & Mobbs, S. D. 1999 Experimental studies of strongly stratified flow past three-dimensional orography. J. Fluid Mech. 390, 223–249.Google Scholar
Williamson, C. H. K. 1996 Three-dimensional wake transition. J. Fluid Mech. 328, 345–407.Google Scholar
Wu, J. 1969 Mixed region collapse with internal wave generation in a density-stratified medium. J. Fluid Mech. 35, 531–544.Google Scholar