Hostname: page-component-745bb68f8f-cphqk Total loading time: 0 Render date: 2025-02-11T12:22:44.729Z Has data issue: false hasContentIssue false
  • English
  • Français

Internal solitary wave generation by tidal flow over topography

Published online by Cambridge University Press:  29 January 2018

R. Grimshaw Open the ORCID record for R. Grimshaw [Opens in a new window]  and
K. R. Helfrich
R. Grimshaw*
Affiliation:
Department of Mathematics, University College London, WC1E 6BT, UK
K. R. Helfrich
Affiliation:
Department of Physical Oceanography, Woods Hole Oceanographic Institution, Woods Hole, MA 02543, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

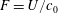Oceanic internal solitary waves are typically generated by barotropic tidal flow over localised topography. Wave generation can be characterised by the Froude number $F=U/c_{0}$, where 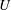$U$ is the tidal flow amplitude and 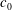$c_{0}$ is the intrinsic linear long wave phase speed, that is the speed in the absence of the tidal current. For steady tidal flow in the resonant regime, 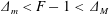$\unicode[STIX]{x1D6E5}_{m}<F-1<\unicode[STIX]{x1D6E5}_{M}$, a theory based on the forced Korteweg–de Vries equation shows that upstream and downstream propagating undular bores are produced. The bandwidth limits 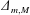$\unicode[STIX]{x1D6E5}_{m,M}$ depend on the height (or depth) of the topographic forcing term, which can be either positive or negative depending on whether the topography is equivalent to a hole or a sill. Here the wave generation process is studied numerically using a forced Korteweg–de Vries equation model with time-dependent Froude number, 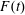$F(t)$, representative of realistic tidal flow. The response depends on 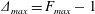$\unicode[STIX]{x1D6E5}_{max}=F_{max}-1$, where 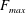$F_{max}$ is the maximum of 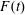$F(t)$ over half of a tidal cycle. When 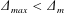$\unicode[STIX]{x1D6E5}_{max}<\unicode[STIX]{x1D6E5}_{m}$ the flow is always subcritical and internal solitary waves appear after release of the downstream disturbance. When 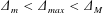$\unicode[STIX]{x1D6E5}_{m}<\unicode[STIX]{x1D6E5}_{max}<\unicode[STIX]{x1D6E5}_{M}$ the flow reaches criticality at its peak, producing upstream and downstream undular bores that are released as the tide slackens. When 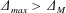$\unicode[STIX]{x1D6E5}_{max}>\unicode[STIX]{x1D6E5}_{M}$ the tidal flow goes through the resonant regime twice, producing undular bores with each passage. The numerical simulations are for both symmetrical topography, and for asymmetric topography representative of Stellwagen Bank and Knight Inlet.

JFM classification

Geophysical and Geological Flows: Internal waves Waves/Free-surface Flows: Solitary waves Geophysical and Geological Flows: Topographic effects
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 839 , 25 March 2018 , pp. 387 - 407
Check for updates
Copyright
© 2018 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Akylas, T., Grimshaw, R., Clark, S. & Tabaei, A. 2007 Reflecting tidal wave beams and local generation of solitary waves in the ocean thermocline. J. Fluid Mech. 593, 297–313.Google Scholar
Armi, L. & Farmer, D. 2002 Stratified flow over topography: bifurcation fronts and transition to the uncontrolled state. Proc. R. Soc. Lond. A 458, 513–538.Google Scholar
Buijsman, M. C., Kanarska, Y. & McWilliams, J. C. 2010 On the generation and evolution of nonlinear internal waves in the South China Sea. J. Geophys. Res. 115, C02012.Google Scholar
Cai, S., Long, X. & Gan, Z. 2002 A numerical study of the generation and propagation of internal solitary waves in the Luzon Strait. Oceanol. Acta 25, 51–60.Google Scholar
Chen, G.-Y., Liu, C.-T., Wang, Y.-H. & Hsu, M. K. 2011 Interaction and generation of long-crested internal solitary waves in the South China Sea. J. Geophys. Res. 116, C06013.Google Scholar
Cummins, P. F. & Armi, L. 2010 Upstream internal jumps in stratified sill flow: observations of formation. J. Phys. Oceanogr. 40, 1419–1426.Google Scholar
Cummins, P. F., Armi, L. & Vagle, S. 2006 Upstream internal hydraulic jumps. J. Phys. Oceanogr. 36, 753–769.Google Scholar
Cummins, P., Vagle, S., Armi, L. & Farmer, D. 2003 Stratified flow over topography: upstream influence and generation of nonlinear internal waves. Proc. R. Soc. Lond. A 459, 1467–1487.Google Scholar
Duda, T. F., Lynch, J. F., Irish, J. D., Beardsley, R. C., Ramp, S. R., Chiu, C. S., Tang, T. Y. & Yang, Y. J. 2004 Internal tide and nonlinear internal wave behavior at the continental slope in the northern South China Sea. IEEE J. Ocean. Engng 29, 1105–1130.Google Scholar
Farmer, D. M. & Armi, L. 1999a The generation and trapping of solitary waves over topography. Science 283, 188–190.CrossRefGoogle ScholarPubMed
Farmer, D. M. & Armi, L. 1999b Stratified flow over topography: the role of small scale entrainment and mixing in flow establishment. Proc. R. Soc. Lond. A 455, 3221–3258.Google Scholar
Farmer, D. M. & Armi, L. 2001 Stratified flow over topography: models versus observations. Proc. R. Soc. Lond. A 457, 267–280.Google Scholar
Farmer, D. M. & Smith, J. D 1980 Tidal interaction of stratified flow with a sill in Knight Inlet. Deep-Sea Res. A 27, 239–254.Google Scholar
Gerkema, T. 2001 Internal and interfacial tides: beam scattering and local generation of solitary waves. J. Mar. Res. 59, 227–255.Google Scholar
Grimshaw, R. 2010 Transcritical flow past an obstacle. ANZIAM J. 52, 1–25.Google Scholar
Grimshaw, R., Pelinovsky, E. & Talipova, T. 2007 Modeling internal solitary waves in the coastal ocean. Surv. Geophys. 28, 273–298.Google Scholar
Grimshaw, R., Pelinovsky, E., Talipova, T. & Kurkina, A. 2010 Internal solitary waves: propagation, deformation and disintegration. Nonlinear Process. Geophys. 17, 633–649.Google Scholar
Grimshaw, R. H. J. & Smyth, N. F 1986 Resonant flow of a stratified fluid over topography. J. Fluid Mech. 169, 429–464.Google Scholar
Guo, C., Chen, C., Vlasenko, V. I. & Stashchuk, N. 2011 Numerical investigation of internal solitary waves from the Luzon Strait: generation process, mechanism and three-dimensional effects. Ocean Model. 38, 203–216.Google Scholar
Helfrich, K. R. & Melville, W. K. 2006 Long nonlinear internal waves. Annu. Rev. Fluid Mech. 38, 395–425.Google Scholar
Hibiya, T. 1988 The generation of internal waves by tidal flow over Stellwagen Bank. J. Geophys. Res. 93, 533–542.Google Scholar
Holloway, P., Pelinovsky, E. & Talipova, T. 2001 Internal tide transformation and oceanic internal solitary waves. In Environmental Stratified Flows (ed. Grimshaw, R.), pp. 31–60. Kluwer.Google Scholar
Lai, Z., Chen, C., Cowles, G. W. & Beardsley, R. C. 2010 A nonhydrostatic version of FVCOM. Part 2. Mechanistic study of tidally generated nonlinear internal waves in Massachusetts Bay. J. Geophys. Res. 115, C12049.Google Scholar
Lee, C.-Y. & Beardsley, R. C. 1974 The generation of long nonlinear internal waves in weakly stratified shear flows. J. Geophys. Res. 79, 453–462.Google Scholar
Li, Q. & Farmer, D. M. 2011 The generation and evolution of nonlinear internal waves in the deep basin of the South China Sea. J. Phys. Oceanogr. 41, 1345–1363.CrossRefGoogle Scholar
Liu, A. K., Chang, Y. S., Hsu, M. K. & Liang, N. K. 1998 Evolution of nonlinear internal waves in the East and South China Seas. J. Geophys. Res. 103, 7995–8008.Google Scholar
Liu, A. K., Ramp, S. R., Zhao, Y. & Tswen Yung Tang, T. Y. 2004 A case study of internal solitary wave propagation during ASIAEX 2001. IEEE J. Ocean. Engng 29, 1144–1156.Google Scholar
Liu, Ch-T, Pinkel, R., Klymak, J., Hsu, M. K., Chen, H. W. & Villanoy, C. 2006 Nonlinear internal waves from the Luzon Strait. EOS 87, 449–451.Google Scholar
Maxworthy, T. 1979 A note on the internal solitary waves produced by tidal flow over a three-dimensional ridge. J. Geophys. Res. 84, 338–346.Google Scholar
Melville, W. K. & Helfrich, K. R. 1987 Transcritical two-layer flow over topography. J. Fluid Mech. 178, 31–52.Google Scholar
Orr, M. H. & Mignerey, P. C. 2003 Nonlinear internal waves in the South China Sea: observation of the conversion of depression internal waves to elevation internal waves. J. Geophys. Res. 108(C3), 3064.Google Scholar
Ramp, S. R., Tang, T. Y., Duda, T. F., Lynch, J. F., Liu, A. K., Chiu, C. S., Bahr, F. L., Kim, H. R. & Yang, Y. J. 2004 Internal solitons in the northeastern South China Sea. Part I. Sources and deep water propagation. IEEE J. Ocean. Engng 29, 1157–1181.Google Scholar
Redekopp, L. G. & You, Z. 1995 Passage through resonance for the forced Korteweg–de Vries equation. Phys. Rev. Lett. 74, 5158–6161.Google Scholar
Scotti, A., Beardsley, R. C. & Butman, B. 2007 Generation and propagation of nonlinear internal waves in Massachusetts Bay. J. Geophys. Res. 112, C10001.Google Scholar
Scotti, A., Beardsley, R. C., Butman, B. & Pineda, J. 2008 Shoaling of nonlinear internal waves in Massachusetts Bay. J. Geophys. Res. 113, C08031.Google Scholar
Stashchuk, N. & Vlasenko, V. I. 2007 Numerical modelling of stratified tidal flow over a fjord sill. Ocean Dyn. 57, 325–338.Google Scholar
Stastna, M. & Peltier, W. R. 2004 Upstream-propagating solitary waves and forced internal-wave breaking in stratified flow over a sill. Proc. R. Soc. Lond. A 460, 3159–3190.Google Scholar
Stastna, M. & Peltier, W. R. 2005 On the resonant generation of large-amplitude internal solitary and solitary-like waves. J. Fluid Mech. 543, 267–292.Google Scholar
Vlasenko, V. I., Guo, C. & Stashchuk, N. 2012 On the mechanism of A-type and B-type internal solitary wave generation in the northern South China Sea. Deep-Sea Res. I 69, 100–112.Google Scholar
Vlasenko, V. I., Stashchuk, N., Guo, C. & Chen, X. 2010 Multimodal structure of baroclinic tides in the South China Sea. Nonlinear Process. Geophys. 17, 529–543.Google Scholar
Warn-Varnas, A., Hawkins, J., Lamb, K. G., Piacsek, S., Chin-Bing, S., King, D. & Burgos, G 2010 Solitary wave generation dynamics at Luzon Strait. Ocean Model. 31, 9–27.Google Scholar
Williamson, J. H. 1980 Low-storage Runge–Kutta schemes. J. Comput. Phys. 35, 48–56.Google Scholar
Zhao, Z. & Alford, M. H. 2006 Source and propagation of internal solitary waves in the northeastern South China Sea. J. Geophys. Res. 111, C11012.Google Scholar