Published online by Cambridge University Press: 10 August 2017
In this work, we analyse the internal shear layer structures generated by the libration of an axisymmetric object in an unbounded fluid rotating at a rotation rate 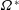 $\unicode[STIX]{x1D6FA}^{\ast }$ using direct numerical simulation and small Ekman number asymptotic analysis. We consider weak libration amplitude and libration frequency
$\unicode[STIX]{x1D6FA}^{\ast }$ using direct numerical simulation and small Ekman number asymptotic analysis. We consider weak libration amplitude and libration frequency 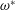 $\unicode[STIX]{x1D714}^{\ast }$ within the inertial wave interval
$\unicode[STIX]{x1D714}^{\ast }$ within the inertial wave interval 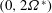 $(0,2\unicode[STIX]{x1D6FA}^{\ast })$ such that the fluid dynamics is mainly described by a linear axisymmetric harmonic solution. The internal shear layer structures appear along the characteristic cones of angle
$(0,2\unicode[STIX]{x1D6FA}^{\ast })$ such that the fluid dynamics is mainly described by a linear axisymmetric harmonic solution. The internal shear layer structures appear along the characteristic cones of angle 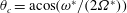 $\unicode[STIX]{x1D703}_{c}=\text{acos}(\unicode[STIX]{x1D714}^{\ast }/(2\unicode[STIX]{x1D6FA}^{\ast }))$ which are tangent to the librating object at so-called critical latitudes. These layers correspond to thin viscous regions where the singularities of the inviscid solution are smoothed. We assume that the velocity field in these layers is described by the class of similarity solutions introduced by Moore & Saffman (Phil. Trans. R. Soc. Lond. A, vol. 264, 1969, pp. 597–634). These solutions are characterized by two parameters only: a real parameter
$\unicode[STIX]{x1D703}_{c}=\text{acos}(\unicode[STIX]{x1D714}^{\ast }/(2\unicode[STIX]{x1D6FA}^{\ast }))$ which are tangent to the librating object at so-called critical latitudes. These layers correspond to thin viscous regions where the singularities of the inviscid solution are smoothed. We assume that the velocity field in these layers is described by the class of similarity solutions introduced by Moore & Saffman (Phil. Trans. R. Soc. Lond. A, vol. 264, 1969, pp. 597–634). These solutions are characterized by two parameters only: a real parameter 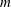 $m$, which measures the strength of the underlying singularity, and a complex amplitude coefficient
$m$, which measures the strength of the underlying singularity, and a complex amplitude coefficient 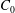 $C_{0}$. We first analyse the case of a disk for which a general asymptotic solution for small Ekman numbers is known when the disk is in a solid plane. We demonstrate that the numerical solutions obtained for a free disk and for a disk in a solid plane are both well described by the asymptotic solution and by its similarity form within the internal shear layers. For the disk, we obtain a parameter
$C_{0}$. We first analyse the case of a disk for which a general asymptotic solution for small Ekman numbers is known when the disk is in a solid plane. We demonstrate that the numerical solutions obtained for a free disk and for a disk in a solid plane are both well described by the asymptotic solution and by its similarity form within the internal shear layers. For the disk, we obtain a parameter 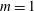 $m=1$ corresponding to a Dirac source at the edge of the disk and a coefficient
$m=1$ corresponding to a Dirac source at the edge of the disk and a coefficient 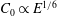 $C_{0}\propto E^{1/6}$ where
$C_{0}\propto E^{1/6}$ where 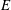 $E$ is the Ekman number. The case of a smoothed librating object such as a spheroid is found to be different. By asymptotically matching the boundary layer solution to similarity solutions close to a critical latitude on the surface, we show that the adequate parameter
$E$ is the Ekman number. The case of a smoothed librating object such as a spheroid is found to be different. By asymptotically matching the boundary layer solution to similarity solutions close to a critical latitude on the surface, we show that the adequate parameter 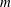 $m$ for the similarity solution is
$m$ for the similarity solution is 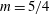 $m=5/4$, leading to a coefficient
$m=5/4$, leading to a coefficient 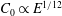 $C_{0}\propto E^{1/12}$, that is larger than for the case of a disk for small Ekman numbers. A simple general expression for
$C_{0}\propto E^{1/12}$, that is larger than for the case of a disk for small Ekman numbers. A simple general expression for 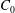 $C_{0}$ valid for any axisymmetric object is obtained as a function of the local curvature radius at the critical latitude in agreement with this change of scaling. This result is tested and validated against direct numerical simulations.
$C_{0}$ valid for any axisymmetric object is obtained as a function of the local curvature radius at the critical latitude in agreement with this change of scaling. This result is tested and validated against direct numerical simulations.