Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-28T22:00:01.816Z Has data issue: false hasContentIssue false
  • English
  • Français

The intermittency boundary in stratified plane Couette flow

Published online by Cambridge University Press:  18 September 2015

Enrico Deusebio ,
C. P. Caulfield  and
J. R. Taylor
Enrico Deusebio
Affiliation:
Department of Applied Mathematics and Theoretical Physics, University of Cambridge, Centre for Mathematical Sciences, Wilberforce Road, Cambridge CB3 0WA, UK
C. P. Caulfield
Affiliation:
Department of Applied Mathematics and Theoretical Physics, University of Cambridge, Centre for Mathematical Sciences, Wilberforce Road, Cambridge CB3 0WA, UK BP Institute, University of Cambridge, Madingley Road, Cambridge CB3 0EZ, UK
J. R. Taylor*
Affiliation:
Department of Applied Mathematics and Theoretical Physics, University of Cambridge, Centre for Mathematical Sciences, Wilberforce Road, Cambridge CB3 0WA, UK
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We study stratified turbulence in plane Couette flow using direct numerical simulations. Two external dimensionless parameters control the dynamics, the Reynolds number 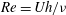$\mathit{Re}=Uh/{\it\nu}$ and the bulk Richardson number 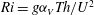$\mathit{Ri}=g{\it\alpha}_{V}Th/U^{2}$, where 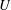$U$ and 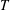$T$ are half the velocity and temperature difference between the two walls respectively, 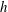$h$ is the half channel depth, ${\it\nu}$ is the kinematic viscosity and 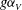$g{\it\alpha}_{V}$ is the buoyancy parameter. We focus on spatio-temporal intermittency due to stratification and we explore the boundary between fully developed turbulence and intermittent flow in the 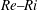$\mathit{Re}{-}\mathit{Ri}$ plane. The structures populating the intermittent flow regime show coexistence between laminar and turbulent patches, and we demonstrate that there are qualitative differences between the previously studied low-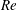$\mathit{Re}$ low-$\mathit{Ri}$ intermittent regime and the high-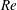$\mathit{Re}$ high-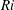$\mathit{Ri}$ intermittent regime. At low-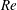$\mathit{Re}$ low-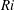$\mathit{Ri}$, turbulent regions span the entire gap, whereas at high-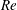$\mathit{Re}$ high-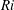$\mathit{Ri}$, turbulence is confined vertically with complex dynamics arising from interacting turbulent layers. Consistent with a previous investigation of Flores & Riley (Boundary-Layer Meteorol., vol. 129 (2), 2010, pp. 241–259), we present evidence suggesting that intermittency in the asymptotic regime of high-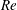$\mathit{Re}$ Couette flows appears for 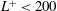$L^{+}<200$, where 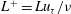$L^{+}=Lu_{{\it\tau}}/{\it\nu}$, with 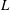$L$ being the Monin–Obukhov length scale, 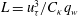$L=u_{{\it\tau}}^{3}/C_{{\it\kappa}}q_{w}$, 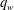$q_{w}$ the wall heat flux, 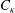$C_{{\it\kappa}}$ the von Kármán constant and 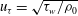$u_{{\it\tau}}=\sqrt{{\it\tau}_{w}/{\it\rho}_{0}}$ the friction velocity determined from the wall shear stress 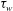${\it\tau}_{w}$, where 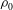${\it\rho}_{0}$ is the constant background density. We also consider the mixing as quantified by various versions of the flux Richardson number 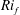$\mathit{Ri}_{f}$, defined as the ratio of the conversion rate from kinetic to potential energy to the turbulent kinetic energy injection rate due to shear. We investigate how laminar and turbulent regions separately contribute to the overall mixing. Remarkably, we find that although fluctuations are greatly suppressed in the laminar regions, 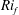$\mathit{Ri}_{f}$ does not change significantly compared with its value in turbulent regions. As we observe a tight coupling between the mean temperature and velocity fields, we demonstrate that both Monin–Obukhov self-similarity theory (Monin & Obukhov, Contrib. Geophys. Inst. Acad. Sci. USSR, vol. 151, 1954, pp. 163–187) and the explicit algebraic model of Lazeroms et al. (J. Fluid Mech., vol. 723, 2013, pp. 91–125) predict the mean profiles well. We thus use these models to trace out the boundary between fully developed turbulence and intermittency in the 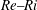$\mathit{Re}{-}\mathit{Ri}$ plane.

JFM classification

Turbulent Flows: Intermittency Turbulent Flows: Stratified turbulence Turbulent Flows: Turbulent Flows
Type
Papers
Information
Journal of Fluid Mechanics , Volume 781 , 25 October 2015 , pp. 298 - 329
Check for updates
Copyright
© 2015 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Ansorge, C. & Mellado, J. P. 2014 Global intermittency and collapsing turbulence in the stratified planetary boundary layer. Boundary-Layer Meteorol. 153 (1), 89–116.CrossRefGoogle Scholar
Armenio, V. & Sarkar, S. 2002 An investigation of stably stratified turbulent channel flow using large-eddy simulation. J. Fluid Mech. 459, 1–42.CrossRefGoogle Scholar
Barkley, D. & Tuckerman, L. S. 2005 Computational study of turbulent laminar patterns in Couette flow. Phys. Rev. Lett. 94 (1), 014502.CrossRefGoogle ScholarPubMed
Barkley, D. & Tuckerman, L. S. 2007 Mean flow of turbulent–laminar patterns in plane Couette flow. J. Fluid Mech. 576, 109–137.Google Scholar
Bewley, T. R.2010 Numerical renaissance: simulation, optimization, and control. Renaissance, San Diego, Calif. (Available at http://numerical-renaissance.com).Google Scholar
Billant, P. & Chomaz, J.-M. 2001 Self-similarity of strongly stratified inviscid flows. Phys. Fluids 13 (6), 1645–1651.CrossRefGoogle Scholar
Brethouwer, G., Billant, P., Lindborg, E. & Chomaz, J.-M. 2007 Scaling analysis and simulation of strongly stratified turbulent flows. J. Fluid Mech. 585, 343–368.Google Scholar
Brethouwer, G., Duguet, Y. & Schlatter, P. 2012 Turbulent–laminar coexistence in wall flows with Coriolis, buoyancy or Lorentz forces. J. Fluid Mech. 704, 137–172.Google Scholar
Businger, J., Wyngaard, J. C., Izumi, Y. & Bradley, E. F. 1971 Flux-profile relationships in the atmospheric surface layer. J. Atmos. Sci. 28 (2), 181–189.Google Scholar
Cenedese, C. & Adduce, C. 2008 Mixing in a density-driven current flowing down a slope in a rotating fluid. J. Fluid Mech. 604, 369–388.CrossRefGoogle Scholar
Chung, D. & Matheou, G. 2012 Direct numerical simulation of stationary homogeneous stratified sheared turbulence. J. Fluid Mech. 696 (410), 434.Google Scholar
Coles, D. 1965 Transition in circular Couette flow. J. Fluid Mech. 21 (03), 385–425.Google Scholar
Corrsin, S. & Kistler, A. L.1955 Free-stream boundaries of turbulent flows. NACA Tech. Rep. 1244.Google Scholar
Deusebio, E., Brethouwer, G., Schlatter, P. & Lindborg, E. 2014 A numerical study of the unstratified and stratified Ekman layer. J. Fluid Mech. 755, 672–704.Google Scholar
Doering, C. R. & Constantin, P. 1992 Energy dissipation in shear driven turbulence. Phys. Rev. Lett. 69 (11), 1648.Google Scholar
Duguet, Y. & Schlatter, P. 2013 Oblique laminar–turbulent interfaces in plane shear flows. Phys. Rev. Lett. 110 (3), 034502.Google Scholar
Duguet, Y., Schlatter, P. & Henningson, D. S. 2010 Formation of turbulent patterns near the onset of transition in plane Couette flow. J. Fluid Mech. 650, 119.Google Scholar
Eaves, T. S. & Caulfield, C. P. 2015 Disruption of SSP/VWI states by a stable stratification. J. Fluid Mech. (submitted).Google Scholar
Flores, O. & Jiménez, J. 2010 Hierarchy of minimal flow units in the logarithmic layer. Phys. Fluids 22 (7), 071704.Google Scholar
Flores, O. & Riley, J. J. 2010 Analysis of turbulence collapse in stably stratified surface layers using direct numerical simulation. Boundary-Layer Meteorol. 129 (2), 241–259.Google Scholar
García-Villalba, M. & del Álamo, J. C. 2011 Turbulence modification by stable stratification in channel flow. Phys. Fluids 23 (4), 045104.Google Scholar
García-Villalba, M., Azagra, E. & Uhlmann, M. 2011 A numerical study of turbulent stably-stratified plane Couette flow. In High Performance Computing in Science and Engineering’10, pp. 251–261. Springer.Google Scholar
Grachev, A. A., Fairall, C. W., Persson, P. O. G., Andreas, E. L. & Guest, P. S. 2005 Stable boundary-layer scaling regimes: the SHEBA data. Boundary-Layer Meteorol. 116 (2), 201–235.Google Scholar
Hamilton, J. H., Kim, J. & Waleffe, F. 1995 Regeneration mechanisms of near-wall turbulence structures. J. Fluid Mech. 287, 317–348.Google Scholar
Holford, J. M. & Linden, P. F. 1999 Turbulent mixing in a stratified fluid. Dyn. Atmos. Oceans 30 (2), 173–198.Google Scholar
Howard, L. N. 1961 Note on a paper of John W. Miles. J. Fluid Mech. 10 (4), 509–512.Google Scholar
Ivey, G. N., Winters, K. B. & Koseff, J. R. 2008 Density stratification, turbulence, but how much mixing? Annu. Rev. Fluid Mech. 40 (1), 169.Google Scholar
Jiménez, J. & Moin, P. 1991 The minimal flow unit in near-wall turbulence. J. Fluid Mech. 225, 213–240.Google Scholar
Jiménez, J. & Pinelli, A. 1999 The autonomous cycle of near-wall turbulence. J. Fluid Mech. 389, 335–359.Google Scholar
Kaimal, J. C., Wyngaard, J. C., Haugen, D. A., Coté, O. R., Izumi, Y., Caughey, S. J. & Readings, C. J. 1976 Turbulence structure in the convective boundary layer. J. Atmos. Sci. 33 (11), 2152–2169.Google Scholar
Karimpour, F. & Venayagamoorthy, S. K. 2015 On turbulent mixing in stably stratified wall-bounded flows. Phys. Fluids 27 (4), 046603.Google Scholar
Kim, J., Moin, P. & Moser, R. 1987 Turbulence statistics in fully developed channel flow at low Reynolds number. J. Fluid Mech. 177, 133–166.Google Scholar
Kondo, J., Kanechika, O. & Yasuda, N. 1978 Heat and momentum transfers under strong stability in the atmospheric surface layer. J. Atmos. Sci. 35 (6), 1012–1021.Google Scholar
Launder, B. E. 1975 On the effects of a gravitational field on the turbulent transport of heat and momentum. J. Fluid Mech. 67 (03), 569–581.Google Scholar
Lazeroms, W. M. J., Brethouwer, G., Wallin, S. & Johansson, A. V. 2013 An explicit algebraic Reynolds-stress and scalar-flux model for stably stratified flows. J. Fluid Mech. 723, 91–125.Google Scholar
Lazeroms, W. M. J., Brethouwer, G., Wallin, S. & Johansson, A. V. 2015 Efficient treatment of the nonlinear features in algebraic Reynolds-stress and heat-flux models for stratified and convective flows. Intl J. Heat Fluid Flow 53 (0), 15–28.CrossRefGoogle Scholar
Lindborg, E. 2006 The energy cascade in a strongly stratified fluid. J. Fluid Mech. 550, 207–242.Google Scholar
Linden, P. F. 1979 Mixing in stratified fluids. Geophys. Astrophys. Fluid Dyn. 13 (1), 3–23.Google Scholar
Mahrt, L., Sun, J., Blumen, W., Delany, T. & Oncley, S. 1998 Nocturnal boundary-layer regimes. Boundary-Layer Meteorol. 88 (2), 255–278.CrossRefGoogle Scholar
Mashayek, A., Caulfield, C. P. & Peltier, W. R. 2013 Time-dependent, non-monotonic mixing in stratified turbulent shear flows: implications for oceanographic estimates of buoyancy flux. J. Fluid Mech. 736, 570–593.Google Scholar
Menter, F. R.1992 Improved two-equation $k$ – ${\it\omega}$ turbulence models for aerodynamic flows. NASA STI/Recon Technical Report 93, 22809.Google Scholar
Miles, J. W. 1961 On the stability of heterogeneous shear flows. J. Fluid Mech. 10 (4), 496–508.Google Scholar
Moin, P. & Mahesh, K. 1998 Direct numerical simulation: a tool in turbulence research. Annu. Rev. Fluid Mech. 30 (1), 539–578.CrossRefGoogle Scholar
Monin, A. S. & Obukhov, A. M. 1954 Basic laws of turbulent mixing in the surface layer of the atmosphere. Contrib. Geophys. Inst. Acad. Sci. USSR 151, 163–187.Google Scholar
Nieuwstadt, F. T. M. 1984 The turbulent structure of the stable, nocturnal boundary layer. J. Atmos. Sci. 41 (14), 2202–2216.Google Scholar
Nieuwstadt, F. T. M. 2005 Direct numerical simulation of stable channel flow at large stability. Boundary-Layer Meteorol. 116, 277–299.Google Scholar
Obukhov, A. M. 1971 Turbulence in an atmosphere with a non-uniform temperature. Boundary-Layer Meteorol. 2 (1), 7–29.Google Scholar
Oglethorpe, R. L. F., Caulfield, C. P. & Woods, A. W. 2013 Spontaneous layering in stratified turbulent Taylor–Couette flow. J. Fluid Mech. 721, R3.Google Scholar
Olvera, D. & Kerswell, R. R.2014 Coherent structures in stratified plane Couette flows. In 67th Annual Meeting of the APS Division of Fluid Dynamics, Bull. Amer. Phys. Soc. 59 (20) San Francisco, California.Google Scholar
Örlü, R. & Schlatter, P. 2011 On the fluctuating wall-shear stress in zero pressure-gradient turbulent boundary layer flows. Phys. Fluids 23 (2), 021704.Google Scholar
Osborn, T. R. 1980 Estimates of the local rate of vertical diffusion from dissipation measurements. J. Phys. Oceanogr. 10 (1), 83–89.Google Scholar
Park, Y. G., Whitehead, J. A. & Gnanadeskian, A. 1994 Turbulent mixing in stratified fluids: layer formation and energetics. J. Fluid Mech. 279, 279–311.Google Scholar
Phillips, O. M. 1972 Turbulence in a strongly stratified fluid – is it unstable? In Deep-Sea Res., vol. 19, pp. 79–81. Elsevier.Google Scholar
Pope, S. B. 1975 A more general effective-viscosity hypothesis. J. Fluid Mech. 72 (02), 331–340.Google Scholar
Pope, S. B. 2000 Turbulent Flows. Cambridge University Press.Google Scholar
Prigent, A., Grégoire, G., Chaté, H., Dauchot, O. & van Saarloos, W. 2002 Large-scale finite-wavelength modulation within turbulent shear flows. Phys. Rev. Lett. 89 (1), 014501.CrossRefGoogle ScholarPubMed
Rodi, W.1976 A new algebraic relation for calculating the Reynolds stresses. In Gesellschaft Angewandte Mathematik und Mechanik Workshop, Paris, France, vol. 56, p. 219.Google Scholar
Rorai, C., Mininni, P. D. & Pouquet, A. 2014 Turbulence comes in bursts in stably stratified flows. Phys. Rev. E 89 (4), 043002.Google Scholar
Ruddick, B. R., McDougall, T. J. & Turner, J. S. 1989 The formation of layers in a uniformly stirred density gradient. Deep-Sea Res. A 36 (4), 597–609.Google Scholar
Salehipour, H. & Peltier, W. R. 2015 Diapycnal diffusivity, turbulent Prandtl number and mixing efficiency in Boussinesq stratified turbulence. J. Fluid Mech. 775, 464–500.Google Scholar
Smyth, W. D., Moum, J. N. & Caldwell, D. R. 2001 The efficiency of mixing in turbulent patches: inferences from direct simulations and microstructure observations. J. Phys. Oceanogr. 31 (8), 1969–1992.Google Scholar
Tang, W., Caulfield, C. P. & Kerswell, R. R. 2009 A prediction for the optimal stratification for turbulent mixing. J. Fluid Mech. 634, 487–497.Google Scholar
Taylor, J. R. 2008 Numerical Simulations of the Stratified Oceanic Bottom Boundary Layer. ProQuest.Google Scholar
Taylor, J. R. & Sarkar, S. 2007 Internal gravity waves generated by a turbulent bottom Ekman layer. J. Fluid Mech. 590, 331–354.Google Scholar
Turner, J. S. 1979 Buoyancy Effects in Fluids. Cambridge University Press.Google Scholar
Wells, M., Cenedese, C. & Caulfield, C. P. 2010 The relationship between flux coefficient and entrainment ratio in density currents. J. Phys. Oceanogr. 40 (12), 2713–2727.Google Scholar
van de Wiel, B. J. H., Moene, A. F. & Jonker, H. J. J. 2012 The cessation of continuous turbulence as precursor of the very stable nocturnal boundary layer. J. Atmos. Sci. 69 (11), 3097–3115.CrossRefGoogle Scholar
van de Wiel, B. J. H., Ronda, R. J., Moene, A. F., Bruin, H. A. R. De. & Holtslag, A. A. M. 2002 Intermittent turbulence and oscillations in the stable boundary layer over land. Part I. A bulk model. J. Atmos. Sci. 59 (5), 942–958.Google Scholar
Wunsch, C. & Ferrari, R. 2004 Vertical mixing, energy, and the general circulation of the oceans. Annu. Rev. Fluid Mech. 36, 281–314.Google Scholar
Wyngaard, J. C. 2010 Turbulence in the atmosphere. In Turbulence in the Atmosphere, vol. 1. Cambridge University Press.Google Scholar
Zilitinkevich, S. S., Elperin, T., Kleeorin, N., Rogachevskii, I., Esau, I., Mauritsen, T. & Miles, M. W. 2008 Turbulence energetics in stably stratified geophysical flows: strong and weak mixing regimes. Q. J. R. Meteorol. Soc. 134 (633), 793–799.Google Scholar