Hostname: page-component-586b7cd67f-2brh9 Total loading time: 0 Render date: 2024-11-23T09:17:06.076Z Has data issue: false hasContentIssue false
  • English
  • Français

Interference effects of three consecutive wall-mounted cubes placed in deep turbulent boundary layer

Published online by Cambridge University Press:  01 September 2014

Hee Chang Lim  and
Masaaki Ohba
Hee Chang Lim*
Affiliation:
School of Mechanical Engineering, Pusan National University, 2, Busandaehak-ro 63beon-gil, Geumjeong-gu, Busan 609-735, South Korea
Masaaki Ohba
Affiliation:
Department of Architecture, Faculty of Engineering, Tokyo Institute of Polytechnics, Atsugi, Kanagawa 243-02/3, Japan
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

In this study we undertook various calculations of the turbulent flow around a building in close proximity to neighbouring obstacles, with the aim of gaining an understanding of the velocity and the surface-pressure variations with respect to the azimuth angle of wind direction and the gap distance between the obstacles. This paper presents the effects of flow interference among consecutive cubes for azimuth angles of 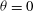$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}\theta = 0$, 15, 30, and 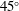$45^{\circ }$ and gap distances of 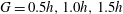$G = 0.5{h}, 1.0{h}, 1.5{h}$, and 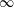$\infty $ (i.e. a single cube), where 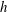$h$ is the cube height, placed in a turbulent boundary layer. A transient detached eddy simulation (DES) was carried out to calculate the highly complicated flow domain around the three wall-mounted cubes to observe the fluctuating pressure, which substantially contributes to the suction pressure when there is separation and reattachment around the leading and trailing edges of the cubes. In addition, the results indicate that an increasing azimuth angle increases the pressure variation on the centre cube of the three parallel-aligned cubes. The mean pressure variation can even change from negative to positive on the side face. Owing to interference effects, the mean pressure coefficient of the centre cube of the three parallel-aligned cubes was generally lower than the coefficient of the single cube and tended to increase depending on the gap distance. Furthermore, when the three consecutive cubes are in a tandem arrangement, the gap distance has little influence on the first cube but results in significant interference effects on the second and third cubes.

JFM classification

Aerodynamics: Flow-structure interactions Wakes/Jets: Separated flows Turbulent Flows: Turbulent boundary layers
Type
Papers
Information
Journal of Fluid Mechanics , Volume 756 , 10 October 2014 , pp. 165 - 190
Copyright
© 2014 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Arie, M., Kiya, M., Moriya, M. & Mori, H. 1983 Pressure fluctuations on the surface of two cylinders in tandem arrangement. Trans. ASME J. Fluids Engng 105, 161–167.CrossRefGoogle Scholar
Australian Standards 1989 SAA loading code Part 2: Wind loads. AS1170.2-1989.Google Scholar
Bailey, P. A. & Kwok, K. C. S. 1985 Interference excitation of twin tall buildings. J. Wind Engng Ind. Aerodyn. 21, 323–338.CrossRefGoogle Scholar
Bearman, P. W. & Wadcock, A. J. 1973 The interaction between a pair of circular cylinders normal to a stream. J. Fluid Mech. 61, 499–511.CrossRefGoogle Scholar
Castro, I. P. & Robins, A. G. 1977 The flow around a surface mounted cube in uniform and turbulent streams. J. Fluid Mech. 79, 307–335.CrossRefGoogle Scholar
Gu, D. & Lim, H. C.2012 Effects of aspect ratio and wind direction on flow characteristics around rectangular obstacles. In 10th UK Conference on Wind Engineering, Southampton, 10–12 September, pp. 163–166.Google Scholar
Hui, Y., Tamura, Y. & Yoshida, A. 2012 Mutual interference effects between two high-rise buildings models with different shapes on local peak pressure coefficients. J. Wind Engng Ind. Aerodyn. 104–106, 98–108.CrossRefGoogle Scholar
Hui, Y., Yoshida, A. & Tamura, Y. 2013 Interference effects between two rectangular-section high-rise buildings on local peak pressure coefficients. J. Wind Engng Ind. Aerodyn. 37, 120–133.Google Scholar
Jeong, T. Y. & Lim, H. C. 2008 Study on the generation of turbulent boundary layer in wind tunnel and the effect of aspect ratio of a rectangular obstacle. Trans. Korean Soc. Mech. Engng 32, 791–799.Google Scholar
Khanduri, A. C., Stathopoulos, T. & Bedard, C. 1998 Wind-induced interference effects on buildings-a review of the state-of-the-art. Engng Struct. 20, 617–630.CrossRefGoogle Scholar
Kim, H. J. & Durbin, P. A. 1988 Investigation of the flow between a pair of circular cylinders in the flopping regime. J. Fluid Mech. 196, 431–448.CrossRefGoogle Scholar
Kim, W., Tamura, Y. & Yoshida, A. 2011 Interference effects on local peak pressures between two buildings. J. Wind Engng Ind. Aerodyn. 99, 584–600.CrossRefGoogle Scholar
Kitagawa, T. & Ohta, H. 2008 Numerical investigation on flow around circular cylinders in tandem arrangement at a subcritical Reynolds number. J. Fluids Struct. 24, 680–699.CrossRefGoogle Scholar
Lim, H. C., Castro, I. P. & Hoxey, R. P. 2007 Bluff bodies in deep turbulent boundary layer: Reynolds number issues. J. Fluid Mech. 571, 97–118.CrossRefGoogle Scholar
Lim, H. C., Thomas, T. G. & Castro, I. P. 2009 Flow around a cube in a turbulent boundary layer: Les and experiment. J. Wind Engng Ind. Aerodyn. 97, 96–109.CrossRefGoogle Scholar
Lozano-Duran, A. & Jimenez, J. 2014 Effect of the computational domain on direct simulations of turbulent channels up to ${R}e_{\tau }=4200$ . Phys. Fluids 26, 011702.CrossRefGoogle Scholar
Martinuzzi, R. & Havel, B. 2000 Turbulent flow around two interfering surface-mounted cubic obstacles in tandem arrangement. Trans. ASME J. Fluids Engng 122, 24–31.CrossRefGoogle Scholar
Maskell, E. C. 1963 A Theory of the Blockage Effects on Bluff Bodies and Stalled Wings in a Closed Wind Tunnel. ARC R&M.Google Scholar
Mercker, E., Cooper, K. R., Fischer, O. & Wiedemann, J. 2005 The influence of a horizontal pressure distribution on aerodynamic drag in open and closed wind tunnels. SAE Trans. 114, 921–938.Google Scholar
Nozawa, K. & Tamura, T. 2002 Large eddy simulation of the flow around a low-rise building immersed in a rough-wall turbulent boundary layer. J. Wind Engng Ind. Aerodyn. 90, 1151–1162.CrossRefGoogle Scholar
Ricciardelli, F. & Vickery, B. J. 1998 The aerodynamic characteristics of twin column. Wind Struct. 1, 225–241.CrossRefGoogle Scholar
Richards, P. J., Hoxey, R. P. & Short, L. J. 2001 Wind pressure on a 6m cube. J. Wind Engng Ind. Aerodyn. 89, 1553–1564.CrossRefGoogle Scholar
Sakamoto, H. & Haniu, H. 1988 Effect of free-stream turbulence on characteristics of fluctuating forces acting on two square prisms in tandem arrangement. Trans. ASME J. Fluids Engng 110, 140–146.CrossRefGoogle Scholar
Salim, S. M. & Cheah, S. C. 2009 Wall $y^+$ strategy for dealing with wall-bounded turbulent flows. In Proceedings of the International MultiConference of Engineers and Computer Scientists, IMECS 2009, Hong Kong (ed. Ao, S. I., Castillo, O., Douglas, C., Feng, D. D. & Lee, J.-A.). Newswood Limited.Google Scholar
Saunders, J. W. & Melbourne, W. H. 1979 Buffeting effects of upstream buildings. In Proceedings of the Fifth International Conference on Wind Engineering, Fort Collins, Colorado, pp. 593–606. Pergamon Press.Google Scholar
Shah, K. B. & Ferziger, J. H. 1997 A fluid mechanician’s view of wind engineering: large-eddy simulation of flow past a cubical obstacle. J. Wind Engng Ind. Aerodyn. 67–68, 211–224.CrossRefGoogle Scholar
Squires, K. D. 2004 Detached-Eddy Simulation: Current Status and Perspectives. Springer.Google Scholar
Sumner, D., Price, S. J. & Paidoussis, M. P.1998 Investigation of side-by-side circular cylinders in steady cross-flow by particle image velocimetry. In Proceedings 1998 ASME Fluids Engineering, Division Summer Meeting, vol. 1 (ed. American Society of Mechanical Engineers), p. 37. ASME.Google Scholar
Sumner, D., Price, S. J. & Paidoussis, M. P. 1999 Tandem cylinders in impulsively started flow. J. Fluids Struct. 13, 955–965.CrossRefGoogle Scholar
Sumner, D., Richards, M. D. & Akosile, O. O. 2005 Two staggered circular cylinders of equal diameter in cross-flow. J. Fluids Struct. 20, 255–276.CrossRefGoogle Scholar
Tang, U. F. & Kwok, K. C. S. 2004 Interference excitation mechanisms on a 3DOF aeroelastic CAARC building model. J. Wind Engng Ind. Aerodyn. 92, 1299–1314.CrossRefGoogle Scholar
Thepmongkorn, S., Wood, G. S. & Kwok, K. C. S. 2002 Interference effects on wind-induced coupled motion of a tall building. J. Wind Engng Ind. Aerodyn. 90, 1807–1815.CrossRefGoogle Scholar
Thool, K. P., Ashok, K. A. & Anupam, C. 2013 Effect of interference on wind loads on tall buildings. J. Acad. Indus. Res. 1 (12), 758–760.Google Scholar
Tieleman, H. W. & Akins, R. E. 1996 The effect of incident turbulence on the surface pressures of surface-mounted prisms. J. Fluids Struct. 10, 367–393.CrossRefGoogle Scholar
To, A. P. & Lam, K. M. 2003 Wind-induced interference effects on a group of buildings. In 11th International Conference on Wind Engineering, Texas Tech University, Lubbock, TX, vol. 1 (ed. Smith, D. A. & Letchford, C. W.), pp. 2405–2410. IAWE.Google Scholar
Williamson, C. H. K. 1985 Evolution of a single wake behind a pair of bluff bodies. Trans. ASME J. Fluids Engng 159, 1–18.Google Scholar
Xie, Z. T. & Castro, I. P. 2008 Efficient generation of inflow conditions for large-eddy simulations of street-scale flows. J. Flow Turb. Combus. 81, 449–470.CrossRefGoogle Scholar
Xie, Z. N. & Gu, M. 2004 Mean interference effects among tall building. Engng Struct. 26, 1173–1183.CrossRefGoogle Scholar
Xie, Z. N. & Gu, M. 2007 Simplified formulas for evaluation of wind-induced interference effects among three tall building. J. Wind Engng Ind. Aerodyn. 95, 31–52.CrossRefGoogle Scholar
Yakhot, A., Anor, T., Liu, H. & Nikitin, N. 2006 Direct numerical simulation of turbulent flow around a wall-mounted cube: spatio-temporal evolution of large-scale vortices. J. Fluid Mech. 566, 1–9.CrossRefGoogle Scholar
Zdravkovich, M. M. 1977 Review of flow interference between two circular cylinders in various arrangements. Trans. ASME J. Fluids Engng 99, 618–633.CrossRefGoogle Scholar
Zdravkovich, M. M. 1987 The effects of interference between circular cylinders in cross flow. J. Fluids Struct. 1, 239–261.CrossRefGoogle Scholar
Zhang, W. J. & Kwok, K. C. S. 1994 Aeroelastic torsional behaviour of tall buildings in wakes. J. Wind Engng Ind. Aerodyn. 51, 229–248.CrossRefGoogle Scholar