Published online by Cambridge University Press: 16 March 2023
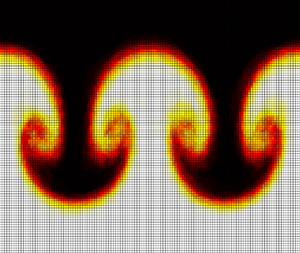
We derive interface models for three-dimensional Rayleigh–Taylor instability (RTI), making use of a novel asymptotic expansion in the non-locality of the fluid flow. These interface models are derived for the purpose of studying universal features associated with RTI such as the Froude number in single-mode RTI, the predicted quadratic growth of the interface amplitude under multi-mode random perturbations, the optimal (viscous) mixing rates induced by the RTI and the self-similarity of horizontally averaged density profiles and the remarkable stabilization of the mixing layer growth rate which arises for the three-fluid two-interface heavy–light–heavy configuration, in which the addition of a third fluid bulk slows the growth of the mixing layer to a linear rate. Our interface models can capture the formation of small-scale structures induced by severe interface roll-up, reproduce experimental data in a number of different regimes and study the effects of multiple interface interactions even as the interface separation distance becomes exceedingly small. Compared with traditional numerical schemes used to study such phenomena, our models provide a computational speed-up of at least two orders of magnitude.