Hostname: page-component-586b7cd67f-t8hqh Total loading time: 0 Render date: 2024-11-26T11:43:28.808Z Has data issue: false hasContentIssue false
  • English
  • Français

Interactions of a streamwise-oriented vortex with a finite wing

Published online by Cambridge University Press:  24 February 2015

D. J. Garmann  and
M. R. Visbal
D. J. Garmann*
Affiliation:
Air Force Research Laboratory, Wright–Patterson AFB, OH 45433, USA
M. R. Visbal
Affiliation:
Air Force Research Laboratory, Wright–Patterson AFB, OH 45433, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

A canonical study is developed to investigate the unsteady interactions of a streamwise-oriented vortex impinging upon a finite surface using high-fidelity simulation. As a model problem, an analytically defined vortex superimposed on a free stream is convected towards an aspect-ratio-six (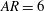$\mathit{AR}=6$) plate oriented at an angle of 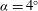${\it\alpha}=4^{\circ }$ and Reynolds number of 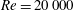$\mathit{Re}=20\,000$ in order to characterize the unsteady modes of interaction resulting from different spanwise positions of the incoming vortex. Outboard, tip-aligned and inboard positioning are shown to produce three distinct flow regimes: when the vortex is positioned outboard of, but in close proximity to, the wingtip, it pairs with the tip vortex to form a dipole that propels itself away from the plate through mutual induction, and also leads to an enhancement of the tip vortex. When the incoming vortex is aligned with the wingtip, the tip vortex is initially strengthened by the proximity of the incident vortex, but both structures attenuate into the wake as instabilities arise in the pair’s feeding sheets from the entrainment of opposite-signed vorticity into either structure. Finally, when the incident vortex is positioned inboard of the wingtip, the vortex bifurcates in the time-mean sense with portions convecting above and below the wing, and the tip vortex is mostly suppressed. The time-mean bifurcation is actually a result of an unsteady spiralling instability in the vortex core that reorients the vortex as it impacts the leading edge, pinches off, and alternately attaches to either side of the wing. The increased effective angle of attack inboard of impingement enhances the three-dimensional recirculation region created by the separated boundary layer off the leading edge which draws fluid from the incident vortex inboard and diminishes its impact on the outboard section of the wing. The slight but remaining downwash present outboard of impingement reduces the effective angle of attack in that region, resulting in a small separation bubble on either side of the wing in the time-mean solution, effectively unloading the tip outboard of impingement and suppressing the tip vortex. All incident vortex positions provide substantial increases in the wing’s lift-to-drag ratio; however, significant sustained rolling moments also result. As the vortex is brought inboard, the rolling moment diminishes and eventually switches sign as the reduced outboard loading balances the augmented sectional lift inboard of impingement.

JFM classification

Vortex Flows: Vortex dynamics Vortex Flows: Vortex Flows Vortex Flows: Vortex interactions
Type
Papers
Information
Journal of Fluid Mechanics , Volume 767 , 25 March 2015 , pp. 782 - 810
Check for updates
Copyright
© Cambridge University Press 2015. This is a work of the U.S. Government and is not subject to copyright protection in the United States. 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Alpert, P. 1981 Implicit filtering in conjunction with explicit filtering. J. Comput. Phys. 44 (1), 212–219.Google Scholar
Barnes, C. J., Visbal, M. R. & Gordnier, R. E. 2015 Analysis of streamwise-oriented vortex interactions for two wings in close proximity. Phys. Fluids 27 (015103).CrossRefGoogle Scholar
Batchelor, G. 1964 Axial flow in trailing line vortices. J. Fluid Mech. 20 (4), 645–658.CrossRefGoogle Scholar
Beam, R. & Warming, R. 1978 An implicit factored scheme for the compressible Navier–Stokes equations. AIAA J. 16 (4), 393–402.Google Scholar
Beukenberg, M. & Hummel, D.1990 Aerodynamics, performance and control of airplanes in formation flight. In Proceedings of the 17th Congress of the International Council of the Aeronautical Sciences, Vol. 2, pp. 1777–1794.Google Scholar
Choi, H. & Moin, P. 1994 Effects of the computational time step on numerical solutions of turbulent flow. J. Comput. Phys. 113 (1), 1–4.Google Scholar
Crow, S. C. 1970 Stability theory of a pair of training vortices. AIAA J. 8, 2172–2179.Google Scholar
Gaitonde, D. & Visbal, M.1998 High-order schemes for Navier–Stokes equations: algorithm and implementation into FDL3DI. Tech. Rep. AFRL-VA-WP-TR-1998-3060. Air Force Research Laboratory, Wright–Patterson AFB.CrossRefGoogle Scholar
Gaitonde, D. & Visbal, M.1999 Further development of a Navier–Stokes solution procedure based on higher-order formulas. AIAA Paper 99-0557. AIAA.CrossRefGoogle Scholar
Garmann, D. J. & Visbal, M. R.2014 Interaction of a streamwise-oriented vortex with a wing. AIAA Paper 2014-1282. AIAA.Google Scholar
Garmann, D., Visbal, M. & Orkwis, P. 2013 Comparative study of implicit and subgrid-scale model large-eddy simulation techniques for low-Reynolds number airfoil applications. Intl J. Numer. Meth. Fluids 71 (12), 1546–1565.CrossRefGoogle Scholar
Georgiadis, N. J., Rizzetta, D. P. & Fureby, C. 2010 Large-eddy simulation: current capabilities, recommended practices, and future research. AIAA J. 48 (8), 1772–1784.Google Scholar
Gordnier, R. E. & Visbal, M. R. 1999 Numerical simulation of the impingement of streamwise vortex on a plate. Intl J. Comput. Fluid Dyn. 12 (1), 49–66.Google Scholar
Gursul, I. & Xie, W. 2001 Interaction of vortex breakdown with an oscillating fin. AIAA J. 39 (3), 438–446.Google Scholar
Heyes, A. L., Jones, R. F. & Smith, D. A. R.2004 Wandering of wing-tip vortices. In 12th International Symposium on Application of Laser Techniques to Fluid Mechanics. Lisbon, Portugal.Google Scholar
Hummel, D. 1983 Aerodynamic aspects of formation flight in birds. J. Theor. Biol. 104 (3), 321–347.Google Scholar
Hummel, D. 1995 Formation flight as an energy-saving mechanism. Isr. J. Zool. 41 (3), 261–278.Google Scholar
Inasawa, A., Mori, F. & Asai, M. 2012 Detailed observations of interactions of wingtip vortices in close-formation flight. J. Aircraft 49 (1), 206–213.Google Scholar
Jacquin, L., Fabre, D. & Geffroy, P.2001 The properties of a transport aircraft wake in the extended near field: an experimental study. AIAA Paper 2001-1038. AIAA.CrossRefGoogle Scholar
Jacquin, L. & Pantano, C. 2002 On the persistence of trailing vortices. J. Fluid Mech. 471, 159–168.Google Scholar
Jameson, A., Schmidt, W. & Turkel, E.1981 Numerical solutions of the Euler equations by finite volume methods using Runge–Kutta time stepping schemes. AIAA Paper 1981-1259. AIAA.Google Scholar
Kless, J., Aftosmis, M. J., Ning, S. A. & Nemec, M. 2013 Inviscid analysis of extended-formation flight. AIAA J. 51 (7), 1703–1715.Google Scholar
Lambert, C. & Gursul, I. 2004 Characteristics of fin buffeting over delta wings. J. Fluids Struct. 19 (3), 307–319.Google Scholar
Leibovich, S. & Stewartson, K. 1983 A sufficient condition for the instability of columnar vortices. J. Fluid Mech. 126, 335–356.Google Scholar
Lele, S. 1992 Compact finite difference schemes with spectral-like resolution. J. Comput. Phys. 103 (1), 16–42.Google Scholar
Lissaman, P. B. S. & Shollenberger, C. A. 1970 Formation flight of birds. Science 168 (3934), 1003–1005.Google Scholar
Matthew, J., Lechner, R., Foysi, H., Sesterhenn, J. & Friedrich, R. 2003 An explicit filtering method for LES of compressible flows. Phys. Fluids 15 (8), 2279–2289.CrossRefGoogle Scholar
Ning, S. A., Flanzer, T. C. & Kroo, I. M.2010 Aerodynamic performance of extended formation flight. AIAA Paper 2010-1240. AIAA.Google Scholar
Pulliam, T. 1986 Artificial dissipation models for the Euler equations. AIAA J. 24 (12), 1931–1940.Google Scholar
Pulliam, T. & Chaussee, D. 1981 A diagonal form of an implicit approximate-factorization algorithm. J. Comput. Phys. 17 (10), 347–363.Google Scholar
Richez, A., Le Pape, A., Costes, M. & Gavériaux, R.2012 Zonal detatched-eddy simulation (ZDES) of the three-dimensional stalled flow around a finite span wing. AIAA Paper 2012-3281. AIAA.Google Scholar
Rizzetta, D. P., Visbal, M. R. & Morgan, P. E.2008 A high-order compact finite-difference scheme for large-eddy simulation of active flow control (invited). AIAA Paper 2008-526. AIAA.Google Scholar
Rockwell, D. 1998 Vortex–body interactions. Annu. Rev. Fluid Mech. 30, 199–229.Google Scholar
Sherer, S. & Scott, J. 2005 High-order compact finite-difference methods on general overset grids. J. Comput. Phys. 210 (2), 459–496.Google Scholar
Slotnick, J. P., Clark, R. W., Friedman, D. M., Yadlin, Y., Yeh, D. T., Carr, J. E., Czech, M. J. & Bieniawski, S. W.2014 Computational aerodynamic analysis for the formation flight for aerodynamic benefit program. AIAA Paper 2014-1458. AIAA.Google Scholar
Steger, J., Dougherty, F. & Benek, J. 1983 A Chimera grid scheme. In Advances in Grid Generation (ed. Ghia, K. & Ghia, U.), vol. 5, pp. 59–69. American Society of Mechanical Engineers.Google Scholar
Stolz, S. & Adams, N. 1999 An approximate deconvolution procedure for large-eddy simulation. Phys. Fluids 11 (7), 1699–1701.Google Scholar
Visbal, M. R. & Gaitonde, D. V. 1999 High-order accurate methods for complex unsteady subsonic flows. AIAA J. 37 (10), 1231–1239.CrossRefGoogle Scholar
Visbal, M. & Garmann, D. 2012 Flow structure above stationary and oscillating low-aspect-ratio wings. In Proceedings of the ASME 2012 Fluids Engineering Division Summer Meeting, pp. 1593–1605. American Society of Mechanical Engineers.Google Scholar
Visbal, M. & Gordnier, R.2003 On the structure of the shear layer emanating from a swept leading edge at angle of attack. AIAA Paper 2003–4016. AIAA.Google Scholar
Visbal, M. R., Morgan, P. E. & Rizzetta, D. P.2003 An implicit LES approach based on high-order compact differencing and filtering schemes. AIAA Paper 2003–4098. AIAA.Google Scholar
Visbal, M. R. & Rizzetta, D. P. 2002 Large-eddy simulation on curvilinear grids using compact differencing and filtering schemes. Trans. ASME J. Fluids Engng 124, 836–847.CrossRefGoogle Scholar
Zanotti, A., Ermacora, M., Campanardi, G. & Gibertini, G. 2014 Stereo particle image velocimetry measurements of perpendicular blade–vortex interaction over an oscillating airfoil. Exp. Fluids 55 (9).Google Scholar