Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Amir, Mohammad
Nikora, Vladimir I.
and
Stewart, Mark T.
2014.
Pressure forces on sediment particles in turbulent open-channel flow: a laboratory study.
Journal of Fluid Mechanics,
Vol. 757,
Issue. ,
p.
458.
Sukhodolov, Alexander N.
2015.
Field-based research in fluvial hydraulics: potential, paradigms and challenges.
Journal of Hydraulic Research,
Vol. 53,
Issue. 1,
p.
1.
Aberle, Jochen
and
Järvelä, Juha
2015.
Rivers – Physical, Fluvial and Environmental Processes.
p.
519.
Gibbins, Chris
2015.
Rivers – Physical, Fluvial and Environmental Processes.
p.
479.
Quinlan, Emma
Gibbins, Chris
Malcolm, Iain
Batalla, Ramon
Vericat, Damia
and
Hastie, Lee
2015.
A review of the physical habitat requirements and research priorities needed to underpin conservation of the endangered freshwater pearl mussel Margaritifera margaritifera.
Aquatic Conservation: Marine and Freshwater Ecosystems,
Vol. 25,
Issue. 1,
p.
107.
de Lima, Paulo H. S.
Janzen, Johannes G.
and
Nepf, Heidi M.
2015.
Flow patterns around two neighboring patches of emergent vegetation and possible implications for deposition and vegetation growth.
Environmental Fluid Mechanics,
Vol. 15,
Issue. 4,
p.
881.
Thomas, Robert E.
and
McLelland, Stuart J.
2015.
The impact of macroalgae on mean and turbulent flow fields.
Journal of Hydrodynamics,
Vol. 27,
Issue. 3,
p.
427.
Kubrak, Elżbieta
Kubrak, Janusz
and
Kiczko, Adam
2015.
Experimental Investigation of Kinetic Energy and Momentum Coefficients in Regular Channels with Stiff and Flexible Elements Simulating Submerged Vegetation.
Acta Geophysica,
Vol. 63,
Issue. 5,
p.
1405.
Barkdoll, Brian D.
Kantor, Candice M.
Wesseldyke, Eric S.
and
Ghimire, Santosh R.
2016.
Stormwater Low-Impact Development: A Call to Arms for Hydraulic Engineers.
Journal of Hydraulic Engineering,
Vol. 142,
Issue. 8,
Barsu, Sylvie
Doppler, Delphine
Jerome, J. John Soundar
Rivière, Nicolas
and
Lance, Michel
2016.
Drag measurements in laterally confined 2D canopies: Reconfiguration and sheltering effect.
Physics of Fluids,
Vol. 28,
Issue. 10,
Amir, Mohammad
Nikora, Vladimir
and
Witz, Matthew
2017.
A novel experimental technique and its application to study the effects of particle density and flow submergence on bed particle saltation.
Journal of Hydraulic Research,
Vol. 55,
Issue. 1,
p.
101.
Cameron, S. M.
Nikora, V. I.
and
Stewart, M. T.
2017.
Very-large-scale motions in rough-bed open-channel flow.
Journal of Fluid Mechanics,
Vol. 814,
Issue. ,
p.
416.
Detert, Martin
Johnson, Erika D.
and
Weitbrecht, Volker
2017.
Proof‐of‐concept for low‐cost and non‐contact synoptic airborne river flow measurements.
International Journal of Remote Sensing,
Vol. 38,
Issue. 8-10,
p.
2780.
2017.
Experimental Hydraulics, Vol 1.
p.
237.
Rojas Arques, Santiago
Rubinato, Matteo
Nichols, Andrew
and
Shucksmith, James D.
2018.
Cost effective measuring technique to simultaneously quantify 2D velocity fields and depth-averaged solute concentrations in shallow water flows.
Flow Measurement and Instrumentation,
Vol. 64,
Issue. ,
p.
213.
Boothroyd, Richard J.
Hardy, Richard J.
Warburton, Jeff
and
Marjoribanks, Timothy I.
2018.
The importance of riparian plant orientation in river flow: implications for flow structures and drag.
Journal of Ecohydraulics,
Vol. 3,
Issue. 2,
p.
108.
Vettori, Davide
and
Nikora, Vladimir
2018.
Flow–seaweed interactions: a laboratory study using blade models.
Environmental Fluid Mechanics,
Vol. 18,
Issue. 3,
p.
611.
Young, David L
McFall, Brian C
and
Bryant, Duncan B
2018.
Bubble image velocimetry with a field-deployable acoustic camera.
Measurement Science and Technology,
Vol. 29,
Issue. 12,
p.
125302.
Cornacchia, Loreta
Folkard, Andrew
Davies, Grieg
Grabowski, Robert C.
van de Koppel, Johan
van der Wal, Daphne
Wharton, Geraldene
Puijalon, Sara
and
Bouma, Tjeerd J.
2019.
Plants face the flow in V formation: A study of plant patch alignment in streams.
Limnology and Oceanography,
Vol. 64,
Issue. 3,
p.
1087.
Przyborowski, Łukasz
Łoboda, Anna Maria
and
Bialik, Robert Józef
2019.
Effect of two distinct patches of Myriophyllum species on downstream turbulence in a natural river.
Acta Geophysica,
Vol. 67,
Issue. 3,
p.
987.
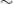 ${\sim }$0.5 m deep) rivers was developed and deployed in the Urie River, Scotland, to study the interactions between turbulent flow and a Ranunculus penicillatus plant patch in its native environment. Statistical moments of the velocity field were calculated utilizing a new method of reducing the contribution of measurement noise, based on the measurement redundancy inherent in the stereoscopic PIV method. Reynolds normal and shear stresses, their budget terms, and higher-order moments of the velocity probability distribution in the wake of the plant patch were found to be dominated by the presence of a free shear layer induced by the plant drag. Plant motion, estimated from the PIV images, was characterized by travelling waves that propagate along the plant with a velocity similar to the eddy convection velocity, suggesting a direct coupling between turbulence and the plant motion. The characteristic frequency of the plant velocity fluctuations (
${\sim }$0.5 m deep) rivers was developed and deployed in the Urie River, Scotland, to study the interactions between turbulent flow and a Ranunculus penicillatus plant patch in its native environment. Statistical moments of the velocity field were calculated utilizing a new method of reducing the contribution of measurement noise, based on the measurement redundancy inherent in the stereoscopic PIV method. Reynolds normal and shear stresses, their budget terms, and higher-order moments of the velocity probability distribution in the wake of the plant patch were found to be dominated by the presence of a free shear layer induced by the plant drag. Plant motion, estimated from the PIV images, was characterized by travelling waves that propagate along the plant with a velocity similar to the eddy convection velocity, suggesting a direct coupling between turbulence and the plant motion. The characteristic frequency of the plant velocity fluctuations (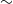 ${\sim }$1 Hz) may suggest that the plant motion is dominated by large eddies with scale similar to the flow depth or plant length. Plant and fluid velocity fluctuations were, in contrast, found to be strongly correlated only over a narrow (
${\sim }$1 Hz) may suggest that the plant motion is dominated by large eddies with scale similar to the flow depth or plant length. Plant and fluid velocity fluctuations were, in contrast, found to be strongly correlated only over a narrow (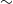 ${\sim }$30 mm) elevation range above the top of the plant, supporting a contribution of the shear layer turbulence to the plant motion. Many aspects of flow–aquatic plant interactions remain to be clarified, and the newly developed stereoscopic field PIV system should prove valuable in future studies.
${\sim }$30 mm) elevation range above the top of the plant, supporting a contribution of the shear layer turbulence to the plant motion. Many aspects of flow–aquatic plant interactions remain to be clarified, and the newly developed stereoscopic field PIV system should prove valuable in future studies.