Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-28T22:00:00.645Z Has data issue: false hasContentIssue false
  • English
  • Français

Interaction of two oscillating bubbles rising in a thin-gap cell: vertical entrainment and interaction with vortices

Published online by Cambridge University Press:  06 February 2020

Audrey Filella ,
Patricia Ern Open the ORCID record for Patricia Ern [Opens in a new window]  and
Veronique Roig Open the ORCID record for Veronique Roig [Opens in a new window]
Audrey Filella
Affiliation:
Institut de Mécanique des Fluides de Toulouse, IMFT, Université de Toulouse, CNRS - Toulouse, France
Patricia Ern*
Affiliation:
Institut de Mécanique des Fluides de Toulouse, IMFT, Université de Toulouse, CNRS - Toulouse, France
Veronique Roig
Affiliation:
Institut de Mécanique des Fluides de Toulouse, IMFT, Université de Toulouse, CNRS - Toulouse, France
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

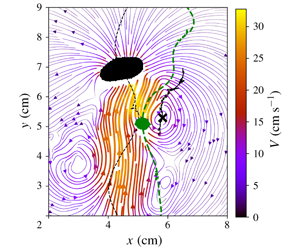
We present an exploratory study of the hydrodynamical interaction between two bubbles rising at high Reynolds numbers in a thin-gap cell. When they are isolated, the bubbles exhibit oscillatory motions and develop an unsteady wake with periodic release of vortices. Experiments combine bubble tracking and measurements of the liquid velocity field through volumetric time-resolved particle image velocimetry. This enabled us to analyse the kinematics of the bubbles during their interaction in relationship with the liquid flow field induced by their motion and governing their behaviour. We first investigate how the kinematics of a bubble, already submitted to the intrinsic instability of its path and wake, is modified by the interaction, i.e. by the presence of a liquid flow field generated by the companion bubble. Two main effects are highlighted in association with (i) the role of the ascending flow generated by the leading bubble, and of its spatial evolution, leading to a slowly varying vertical entrainment of the trailing bubble, and (ii) the role of the vortices released by the leading bubble inducing strong localized horizontal deviations on a bubble in line or in oblique positioning. In the latter case, two major scenarios are identified: deviations of the trailing bubble towards the wake centre line (centring in the wake) or away from it (ejection from the wake). We also show that a regular succession of ejections and re-alignments events may take place (cyclic alternation of ejections and centrings). The analysis is built on the knowledge of the behaviour of isolated bubbles, which is used as the basis for comparison to characterize the effect of the interaction, for the modelling of the vertical entrainment, and for the definition of a criteria on a dimensionless parameter characterizing the ability of a vortex to drive the bubble motion. In turn, we investigate the effect of a bubble passage in the liquid flow field generated by the companion bubble, highlighting the destruction or reinforcement of vortices. We show in particular that both effects can occur without a significant impact on the bubble kinematics.

JFM classification

Drops and Bubbles: Bubble dynamics Vortex Flows: Vortex dynamics Wakes/Jets: Wakes
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 888 , 10 April 2020 , A13
Copyright
© The Author(s), 2020. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bhaga, D. & Weber, M. E. 1980 In-line interaction of a pair of bubbles in a viscous liquid. Chem. Engng Sci. 35 (12), 2467–2474.CrossRefGoogle Scholar
Brosse, N. & Ern, P. 2014 Interaction of two axisymmetric bodies falling in tandem at moderate Reynolds numbers. J. Fluid Mech. 757, 208–230.CrossRefGoogle Scholar
Chen, R. H., Tian, W. X., Su, G. H., Qiu, S. Z., Ishiwatari, Y. & Oka, Y. 2010 Numerical investigation on coalescence of bubble pairs rising in a stagnant liquid. Chem. Engng Sci. (66), 5055–5063.Google Scholar
Cheng, M., Hua, J. & Lou, J. 2010 Simulation of bubble–bubble interaction using a lattice Boltzmann method. Comput. Fluids (39), 260–270.CrossRefGoogle Scholar
Crabtree, J. R. & Bridgwater, J. 1971 Bubble coalescence in viscous liquids. Chem. Engng Sci. 26 (6), 839–851.CrossRefGoogle Scholar
Duineveld, P. C. 1998 Bouncing and coalescence of bubble pairs rising at high Reynolds number in pure water or aqueous surfactant solutions. Appl. Sci. Res. 58, 409–439.CrossRefGoogle Scholar
Filella, A., Ern, P. & Roig, V. 2015 Oscillatory motion and wake of a bubble rising in a thin-gap cell. J. Fluid Mech. 778, 60–88.CrossRefGoogle Scholar
Gumulya, M., Utikar, R. P., Evans, G. M., Joshi, J. B. & Pareek, V. 2017 Interaction of bubbles rising inline in quiescent liquid. Chem. Engng Sci. 166, 1–10.CrossRefGoogle Scholar
Hallez, Y. & Legendre, D. 2011 Interaction between two spherical bubbles rising in a viscous liquid. J. Fluid Mech. 673, 406–431.CrossRefGoogle Scholar
Harper, J. F. 1997 Bubbles rising in line: why is the first approximation so bad? J. Fluid Mech. 351, 289–300.CrossRefGoogle Scholar
Hosokawa, S. & Tomiyama, A. 2006 Effects of bubble wake on coalescence between planar bubbles. J. Fluid Sci. Technol. 1 (2), 94–104.CrossRefGoogle Scholar
Huisman, S. G., Ern, P. & Roig, V. 2012 Interaction and coalescence of large bubbles rising in a thin gap. Phys. Rev. E 85 (2), 027302.Google Scholar
Katz, J. & Meneveau, C. 1996 Wake-induced relative motion of bubbles rising in line. Intl J. Multiphase Flow 22 (2), 239–258.CrossRefGoogle Scholar
Kok, J. B. W. 1993a Dynamics of a pair of gas bubbles moving through liquid. i: theory. Eur. J. Mech. (B Fluids) 12 (4), 515–540.Google Scholar
Kok, J. B. W. 1993b Dynamics of a pair of gas bubbles moving through liquid. II: experiment. Eur. J. Mech. (B Fluids) 12 (4), 541–560.Google Scholar
Komasawa, I., Otake, T. & Kamojima, M. 1980 Wake behavior and its effect on interaction between spherical-cap bubbles. J. Chem. Engng Japan 13 (2), 103–109.CrossRefGoogle Scholar
Kusuno, H. & Sanada, T. 2015 Experimental investigation of the motion of a pair of bubbles at intermediate Reynolds numbers. Multiphase Sci. Technol. 27 (1), 55–66.CrossRefGoogle Scholar
Legendre, D., Magnaudet, J. & Mougin, G. 2003 Hydrodynamic interactions between two spherical bubbles rising side by side in a viscous liquid. J. Fluid Mech. 497, 133–166.CrossRefGoogle Scholar
Magnaudet, J. & Eames, I. 2000 The motion of high-Reynolds-number bubbles in inhomogeneous flows. Annu. Rev. Fluid Mech. 32 (1), 659–708.CrossRefGoogle Scholar
Mougin, G. & Magnaudet, J. 2001 Path instability of a rising bubble. Phys. Rev. Lett. 88 (1), 014502.CrossRefGoogle ScholarPubMed
Mougin, G. & Magnaudet, J. 2006 Wake-induced forces and torques on a zigzagging/spiralling bubble. J. Fluid Mech. 567, 185–194.CrossRefGoogle Scholar
Narayanan, S., Goosens, L. H. J. & Kossen, N. W. F. 1974 Coalescence of two bubbles rising in line at low Reynolds numbers. Chem. Engng Sci. 29, 2071–2082.CrossRefGoogle Scholar
Roig, V., Roudet, M., Risso, F. & Billet, A.-M. 2012 Dynamics of a high-Reynolds-number bubble rising within a thin gap. J. Fluid Mech. 707, 444–466.CrossRefGoogle Scholar
Sanada, T., Sato, A., Shirota, M. & Watanabe, M. 2009 Motion and coalescence of a pair of bubbles rising side by side. Chem. Engng Sci. 64 (11), 2659–2671.CrossRefGoogle Scholar
Sanada, T., Watanabe, M. & Fukano, T. 2006 Interaction and coalescence of bubbles in stagnant liquid. Multiphase Sci. Technol. 18 (2), 155–174.CrossRefGoogle Scholar
Sene, K. J., Hunt, J. C. R. & Thomas, N. H. 1994 The role of coherent structures in bubble transport by turbulent shear flows. J. Fluid Mech. 259, 219–240.CrossRefGoogle Scholar
Smolianski, A., Haari, H. & Luukka, P. 2005 Vortex shedding behind a rising bubble and two-bubble coalescence: a numerical approach. Appl. Math. Model. 29 (7), 15–632.CrossRefGoogle Scholar
Tripathi, M. K., Premlata, A. R., Sahu, K. C. & Govindarajan, R. 2017 Two initially spherical bubbles rising in quiescent liquid. Phys. Rev. Fluids 2, 073601.CrossRefGoogle Scholar
Watanabe, M. & Sanada, T. 2006 In-line motion of a pair of bubbles in a viscous liquid. JSME Intl J. 49 (2), 410–418.CrossRefGoogle Scholar
van Wijngaarden, L. 1993 The mean rise velocity of pairwise-interacting bubbles in liquid. J. Fluid Mech. 251, 55–78.CrossRefGoogle Scholar
Yu, Z., Yang, H. & Fan, L. S. 2011 Numerical simulation of bubble interactions using an adaptive lattice Boltzmann method. Chem. Engng Sci. 66, 3441–3451.CrossRefGoogle Scholar
Yuan, H. & Prosperetti, A. 1994 On the in-line motion of two spherical bubbles in a viscous fluid. J. Fluid Mech. 278, 325–349.CrossRefGoogle Scholar