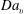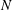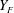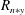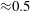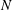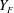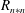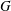1 Introduction
1.1 Motivation and background
Droplet dispersion, vaporization and fuel–air mixing are crucial stages in combustion of liquid fuel sprays in many industrial applications, such as internal combustion engines, gas turbines and rocket engines, and their understanding is central to optimal performance of these devices and for reduction of pollutant emissions. The droplet vaporization rate is the controlling factor for combustion, since vaporization can be the slowest process determining the overall burning rate (Sirignano Reference Sirignano1999). The carrier flow turbulence significantly influences the evaporation process in sprays, either by directly modifying mass and heat transfer or indirectly through droplet dispersion. While the dispersion of droplets can strongly affect droplet vaporization rate, interestingly, strong evaporation may cause time-varying response of the same droplets to carrier-phase velocity fluctuations affecting dispersion. Thus, the mutually coupled phenomena of droplet evaporation, carrier-phase turbulence and macro-scale droplet dispersion govern the micro-scale fuel–air mixing in an evaporating liquid fuel spray. Although there are additional parameters influencing droplet evaporation in complex spray combustion processes, comprehending non-reacting and evaporating flows constitutes a first step. Hence, the understanding of the physics of the interaction between droplet and vapour phases in a polydispersed evaporating spray is the goal of the present paper.
The dispersion of droplets or particles embedded in turbulent flows is a major research field in the two-phase flow community. The studies concerning non-evaporating droplets have focused mainly on the modulation of carrier-phase turbulence by particles (Squires & Eaton Reference Squires and Eaton1990; Boivin, Simonin & Squires Reference Boivin, Simonin and Squires1998; Sundaram & Collins Reference Sundaram and Collins1999; Ferrante & Elghobashi Reference Ferrante and Elghobashi2003; Sahu, Hardalupas & Taylor Reference Sahu, Hardalupas and Taylor2014a
, among others) and/or particle dispersion resulting in preferential accumulation of particles or clustering (Wang & Maxey Reference Wang and Maxey1993; Fessler, Kulick & Eaton Reference Fessler, Kulick and Eaton1994; Wood, Hwang & Eaton Reference Wood, Hwang and Eaton2005; Monchaux, Bourgoin & Cartellier Reference Monchaux, Bourgoin and Cartellier2012; Sahu, Hardalupas & Taylor Reference Sahu, Hardalupas and Taylor2016, among others). Studies concerning droplet evaporation in turbulent flows are mostly based on two-phase simulations (for example, Reveillon & Vervisch Reference Reveillon and Vervisch2000; Colin & Benkenida Reference Colin and Benkenida2003; Patel et al.
Reference Patel, Kirtas, Sankaran and Menon2007; Reveillon & Demoulin Reference Reveillon and Demoulin2007; Apte, Mahesh & Moin Reference Apte, Mahesh and Moin2009; Xia & Luo Reference Xia and Luo2009; Jones, Lyra & Marquis Reference Jones, Lyra and Marquis2010, to name a few). Relatively few experimental studies of evaporative sprays have been documented (for instance, Yule Reference Yule1983; Sommerfeld & Qui Reference Sommerfeld and Qui1998; Nijdam, Starner & Langrish Reference Nijdam, Starner and Langrish2004; Chen, Starner & Masri Reference Chen, Starner and Masri2006; Cochet et al.
Reference Cochet, Bazile, Ferret and Cazin2009). Although the above studies significantly improved our understanding of droplet evaporation and mixing, the influence of turbulent droplet dispersion on droplet evaporation is not well understood, which is mainly due to availability of only limited experimental data to evaluate the assumptions of theoretical models and resulting simulations. In the literature, data on dispersed phase properties (size, velocity etc.), droplet dispersion due to turbulence and mean vapour mass fraction are available mostly for evaporating-droplet-laden turbulent jets and, to a lesser extent, for sprays. However, the link between the spatial distribution of the source of vapour and the fluctuations of vapour mass fraction and its consequence on droplet evaporation have been rarely considered, although it is highly relevant to modelling droplet evaporation in turbulent flows. One of the main input parameters of any non-premixed turbulent combustion model (for instance, Reynolds-averaged Navier–Stokes (RANS) calculations or large eddy simulation (LES)) is the mixture fraction variable (
![]() $Z$
), such that the properties of mixing are characterized with the mean, variance and dissipation rate of the mixture fraction. However, due to the local sources of fuel during droplet vaporization,
$Z$
), such that the properties of mixing are characterized with the mean, variance and dissipation rate of the mixture fraction. However, due to the local sources of fuel during droplet vaporization,
![]() $Z$
is not a conserved scalar, which results in additional unclosed source terms in the transport equations for the mean and variance of
$Z$
is not a conserved scalar, which results in additional unclosed source terms in the transport equations for the mean and variance of
![]() $Z$
(Reveillon & Vervisch Reference Reveillon and Vervisch2000), summarized as follows:
$Z$
(Reveillon & Vervisch Reference Reveillon and Vervisch2000), summarized as follows:
Here, the upper-case and lower-case letters refer respectively to instantaneous and fluctuating quantities for gas velocity (
![]() $U_{g}$
) and vapour mixture fraction (
$U_{g}$
) and vapour mixture fraction (
![]() $Z$
). The
$Z$
). The
![]() $i$
refers to the component of the Cartesian reference system. The overbar denotes time averaging.
$i$
refers to the component of the Cartesian reference system. The overbar denotes time averaging.
![]() $\unicode[STIX]{x1D70C}$
and
$\unicode[STIX]{x1D70C}$
and
![]() $D_{v}$
are the air density and mass diffusivity of fuel vapour in air. The term
$D_{v}$
are the air density and mass diffusivity of fuel vapour in air. The term
![]() $\unicode[STIX]{x1D70C}\overline{\dot{M_{v}}}$
is the Eulerian vaporization rate, which is defined over a control volume (
$\unicode[STIX]{x1D70C}\overline{\dot{M_{v}}}$
is the Eulerian vaporization rate, which is defined over a control volume (
![]() ${\mathcal{V}}$
) corresponding to the ‘subgrid’ description for the spray, and given by
${\mathcal{V}}$
) corresponding to the ‘subgrid’ description for the spray, and given by
where
![]() $N(D)$
is the droplet number density and
$N(D)$
is the droplet number density and
![]() ${\dot{m}}_{v}(D)$
is the droplet evaporation rate of size
${\dot{m}}_{v}(D)$
is the droplet evaporation rate of size
![]() $D$
, and the summation refers to all droplets in a control volume
$D$
, and the summation refers to all droplets in a control volume
![]() ${\mathcal{V}}$
. The terms containing correlations between fluctuations of mixture fraction and Eulerian vaporization rate and gas-phase velocity must be experimentally determined. For a non-reacting and evaporating spray, such correlation terms can be interpreted as the relation between vapour mass fraction, droplet number density and gas velocity, and have significance not only in modelling but also for quantifying the role of instantaneous droplet clustering on droplet evaporation, as explained later. Moreover, for polydispersed sprays, those correlation terms should be determined conditional on droplet size. However, experimental reports on such quantities are non-existent.
${\mathcal{V}}$
. The terms containing correlations between fluctuations of mixture fraction and Eulerian vaporization rate and gas-phase velocity must be experimentally determined. For a non-reacting and evaporating spray, such correlation terms can be interpreted as the relation between vapour mass fraction, droplet number density and gas velocity, and have significance not only in modelling but also for quantifying the role of instantaneous droplet clustering on droplet evaporation, as explained later. Moreover, for polydispersed sprays, those correlation terms should be determined conditional on droplet size. However, experimental reports on such quantities are non-existent.
It should be noted that in order to solve equations (1.1) and (1.2), the evaporation rate of individual droplets appearing in (1.3) is commonly modelled according to the classical
![]() $d^{2}$
-law (the square of the droplet diameter varies linearly with time (Spalding Reference Spalding1951)) or its variants (Miller, Harstad & Bellan Reference Miller, Harstad and Bellan1998). This simple model considers diffusion-controlled evaporation of a single isolated droplet. The effect of forced convection is usually accounted for using the correlations by Ranz & Marshall (Reference Ranz and Marshall1998). However, one of the key assumptions of the model is that the liquid properties at the droplet surface (regression rate, temperature, species concentration) change at rates much slower than those of the gas-phase transport processes. As per the
$d^{2}$
-law (the square of the droplet diameter varies linearly with time (Spalding Reference Spalding1951)) or its variants (Miller, Harstad & Bellan Reference Miller, Harstad and Bellan1998). This simple model considers diffusion-controlled evaporation of a single isolated droplet. The effect of forced convection is usually accounted for using the correlations by Ranz & Marshall (Reference Ranz and Marshall1998). However, one of the key assumptions of the model is that the liquid properties at the droplet surface (regression rate, temperature, species concentration) change at rates much slower than those of the gas-phase transport processes. As per the
![]() $d^{2}$
-law, the evaporation rate of a droplet in a turbulent flow field is expressed as
$d^{2}$
-law, the evaporation rate of a droplet in a turbulent flow field is expressed as
where
![]() $Sh$
and
$Sh$
and
![]() $B$
are the convective Sherwood number and the Spalding transfer number, respectively. The transfer number is expressed as
$B$
are the convective Sherwood number and the Spalding transfer number, respectively. The transfer number is expressed as
![]() $B=(Y_{s}-Y_{\infty })/(1-Y_{s})$
, where
$B=(Y_{s}-Y_{\infty })/(1-Y_{s})$
, where
![]() $Y_{s}$
is the vapour mass fraction at the droplet surface, which is usually assumed to be at saturation state corresponding to droplet temperature, and
$Y_{s}$
is the vapour mass fraction at the droplet surface, which is usually assumed to be at saturation state corresponding to droplet temperature, and
![]() $Y_{\infty }$
is the vapour mass fraction far away from the droplet. However, the appropriate location (with respect to the droplet surface) for defining
$Y_{\infty }$
is the vapour mass fraction far away from the droplet. However, the appropriate location (with respect to the droplet surface) for defining
![]() $Y_{\infty }$
is debatable and usually
$Y_{\infty }$
is debatable and usually
![]() $Y_{\infty }$
is considered to be a constant or sometimes ‘zero’. In reality the mass fraction of vapour away from a droplet need not be ‘zero’ and it may be even a time-varying quantity. However, many simulations consider a constant value for
$Y_{\infty }$
is considered to be a constant or sometimes ‘zero’. In reality the mass fraction of vapour away from a droplet need not be ‘zero’ and it may be even a time-varying quantity. However, many simulations consider a constant value for
![]() $B$
. Also, the droplet vaporization rate is strongly affected due to the presence of neighbouring droplets and so may not be accurately described by the
$B$
. Also, the droplet vaporization rate is strongly affected due to the presence of neighbouring droplets and so may not be accurately described by the
![]() $d^{2}$
-law, i.e. the regression rate of the droplet surface may vary nonlinearly with time. For instance, in their experiments studying the evaporation and mixing processes in a dense spray plume, Rivas & Villermaux (Reference Rivas and Villermaux2016) and Villermaux et al. (Reference Villermaux, Moutte, Amielh and Meunier2017) demonstrated that the lifetime of an individual droplet embedded in a cloud of droplets is much larger than predicted by the conventional
$d^{2}$
-law, i.e. the regression rate of the droplet surface may vary nonlinearly with time. For instance, in their experiments studying the evaporation and mixing processes in a dense spray plume, Rivas & Villermaux (Reference Rivas and Villermaux2016) and Villermaux et al. (Reference Villermaux, Moutte, Amielh and Meunier2017) demonstrated that the lifetime of an individual droplet embedded in a cloud of droplets is much larger than predicted by the conventional
![]() $d^{2}$
-law for a single drop evaporating in a quiescent environment. In a turbulent spray, due to the wide range of the droplet size distribution in sprays, different dynamic behaviour of droplet dispersion and interaction with the surrounding gas leads to formation of instantaneous clusters of droplets in sprays (Zimmer et al.
Reference Zimmer, Domann, Hardalupas and Ikeda2003; Lian, Charalampous & Hardalupas Reference Lian, Charalampous and Hardalupas2013). Droplet clustering can lead to substantial increase in the instantaneous local droplet concentration above the mean value, which causes the inter-droplet spacing to become sufficiently small so that interaction between neighbouring droplets prevents the penetration of oxidizer. Consequently, a fuel-rich mixture is formed in which droplets neither evaporate nor burn individually, but rather in a group. Chiu & coworkers (Chiu & Liu Reference Chiu and Liu1977; Chiu, Kim & Croke Reference Chiu, Kim and Croke1982; Chiu & Kim Reference Chiu and Kim1983) characterized this phenomenon by the group combustion number,
$d^{2}$
-law for a single drop evaporating in a quiescent environment. In a turbulent spray, due to the wide range of the droplet size distribution in sprays, different dynamic behaviour of droplet dispersion and interaction with the surrounding gas leads to formation of instantaneous clusters of droplets in sprays (Zimmer et al.
Reference Zimmer, Domann, Hardalupas and Ikeda2003; Lian, Charalampous & Hardalupas Reference Lian, Charalampous and Hardalupas2013). Droplet clustering can lead to substantial increase in the instantaneous local droplet concentration above the mean value, which causes the inter-droplet spacing to become sufficiently small so that interaction between neighbouring droplets prevents the penetration of oxidizer. Consequently, a fuel-rich mixture is formed in which droplets neither evaporate nor burn individually, but rather in a group. Chiu & coworkers (Chiu & Liu Reference Chiu and Liu1977; Chiu, Kim & Croke Reference Chiu, Kim and Croke1982; Chiu & Kim Reference Chiu and Kim1983) characterized this phenomenon by the group combustion number,
![]() $G$
, which represents the ratio between the characteristic droplet evaporation rate and the molecular inward diffusion rate of oxygen. The magnitude of
$G$
, which represents the ratio between the characteristic droplet evaporation rate and the molecular inward diffusion rate of oxygen. The magnitude of
![]() $G$
has been shown to have a profound effect on flame location and distributions of temperature, fuel vapour and oxygen. However, the experimental quantification of the magnitude of
$G$
has been shown to have a profound effect on flame location and distributions of temperature, fuel vapour and oxygen. However, the experimental quantification of the magnitude of
![]() $G$
is limited in the literature (see Akamatsu et al.
Reference Akamatsu, Mizutani, Katsuki, Tsushima and Cho1996; Chen & Gomez Reference Chen and Gomez1997; Sornek & Dobashi Reference Sornek and Dobashi2000). In (1.4), the Sherwood number depends on the Reynolds number (
$G$
is limited in the literature (see Akamatsu et al.
Reference Akamatsu, Mizutani, Katsuki, Tsushima and Cho1996; Chen & Gomez Reference Chen and Gomez1997; Sornek & Dobashi Reference Sornek and Dobashi2000). In (1.4), the Sherwood number depends on the Reynolds number (
![]() $Re$
) of the droplet such that
$Re$
) of the droplet such that
![]() $Re=\unicode[STIX]{x1D70C}|U_{g}-U|D/\unicode[STIX]{x1D707}$
, where
$Re=\unicode[STIX]{x1D70C}|U_{g}-U|D/\unicode[STIX]{x1D707}$
, where
![]() $\unicode[STIX]{x1D707}$
is the dynamic viscosity of air.
$\unicode[STIX]{x1D707}$
is the dynamic viscosity of air.
![]() $U_{g}-U$
is the instantaneous local droplet–gas slip velocity, which, although it markedly influences the droplet evaporation rate, has been seldom addressed in the past. Important issues, such as alignment of instantaneous vapour clouds with droplet clusters and the role of slip velocity on the correlation between droplets and neighbouring vapour mass fraction, remain to be addressed.
$U_{g}-U$
is the instantaneous local droplet–gas slip velocity, which, although it markedly influences the droplet evaporation rate, has been seldom addressed in the past. Important issues, such as alignment of instantaneous vapour clouds with droplet clusters and the role of slip velocity on the correlation between droplets and neighbouring vapour mass fraction, remain to be addressed.
The above discussion suggests the critical role of experiments to evaluate models for evaporative sprays and also to further explore the two-phase interaction mechanisms. However, the lack of experimental data in this area can be attributed to the challenges encountered in measurement of the dispersed and vapour phases in evaporative sprays. Also, both phases must be simultaneously measured, as required for the quantification of the correlation terms (as described before) and their relation to the local group combustion number. Considering the complexities involved in spray combustion, usually idealized sprays are studied to minimize the coupling between the different effects and to provide parametric results. In this paper, we consider an acetone spray evaporating under ambient atmospheric and non-reacting conditions. Even this apparently simplified configuration poses tough challenges for simultaneous measurements of droplet and vapour phases. In the past, the phase Doppler anemometer (PDA) has been used extensively to measure the dispersed phase (for instance, Hardalupas, Taylor & Whitelaw Reference Hardalupas, Taylor and Whitelaw1990; Hardalupas, Taylor & Whitelaw Reference Hardalupas, Taylor and Whitelaw1994; Sornek, Dobashi & Hirano Reference Sornek, Dobashi and Hirano2000; Nijdam et al. Reference Nijdam, Starner and Langrish2004; Chen et al. Reference Chen, Starner and Masri2006), while planar laser induced fluorescence (PLIF) is usually used for droplet vapour concentration measurements (Bazile & Stepowski Reference Bazile and Stepowski1995; Ritchie & Seitzman Reference Ritchie and Seitzman2001; Cochet et al. Reference Cochet, Bazile, Ferret and Cazin2009). However, for a single particle counter type instrument like the PDA, measurement of instantaneous inter-droplet distance and droplet number density is not straightforward, and also, correlating the single point information of droplet properties with planar measurement of vapour concentration by PLIF is complicated (e.g. Ferrand, Bazile & Boree Reference Ferrand, Bazile and Boree2001). In the present work we use a novel approach of combining the ILIDS (interferometric laser imaging for droplet sizing) and PLIF techniques, as developed by Sahu, Hardalupas & Taylor (Reference Sahu, Hardalupas and Taylor2014b ), for simultaneous droplet and vapour-phase measurements in evaporative sprays. While ILIDS provides instantaneous planar measurements of spatial distributions of individual droplet size, velocity and number density in the spray, the instantaneous vapour mass fraction around the droplets is simultaneously measured by PLIF.
1.2 Scope of the present paper
In this paper we attempt to address some questions of fundamental importance: Can we correlate the instantaneous local vapour mass fraction within a fuel spray to the droplet number density at that instant? What factors influence this correlation? Earlier studies on isolated droplet evaporation suggest that the air turbulence always increases the droplet evaporation rate. Should this be true for droplets in sprays as well? How does preferential segregation of droplets due to clustering affect their evaporation rate? Is there a way to quantify this effect? Accordingly, the objectives of the paper are to (i) quantify the interaction between droplet and vapour phases in a spray and investigate the role of droplet–gas slip velocity and gas phase turbulence on droplet evaporation, (ii) investigate the consequence of droplet dispersion (due to interaction with the surrounding turbulent air flow) on droplet evaporation, (iii) study the effect of droplet cloud formation due to turbulence in sprays on droplet evaporation, in comparison to isolated droplet evaporation, and quantify the group evaporation number and its fluctuations at different radial locations within the spray. The droplet and vapour phases are simultaneously characterized by application of the combined ILIDS and PLIF techniques to an evaporating acetone spray. The measurement region is situated 350 mm below the atomizer, where strong interaction of the droplets with the entrained air flow is expected and the memory of the liquid break-up processes during the atomization is no longer influential. The measurement areas correspond to four different radial locations beginning from the spray axis. Apart from presenting the results, including basic statistical quantities (e.g. mean and standard deviation of droplet size, velocity and vapour mass fraction), the correlations between vapour mass fraction and droplet number density and droplet velocity are presented conditional on droplet size classes for the first time. Measurement of such statistics is vital for further understanding of the underlying physics of the two-phase interaction mechanisms, and also useful for developing models for the unclosed terms in (1.1) and (1.2). The instantaneous group evaporation number (
![]() $G$
) of the droplets is quantified from the measurements, and its link with the above correlations is established to understand the prevailing modes of group evaporation in the spray. The next section (§ 2) describes the experimental arrangement and measurement techniques used in this study. The results are presented in § 3. The mean and fluctuating characteristics of the two phases are presented in § 3.2 and the results of the measurements of specified spatial correlations are discussed in § 3.3, together with the measured group evaporation number. A summary of the main findings can be found in § 4.
$G$
) of the droplets is quantified from the measurements, and its link with the above correlations is established to understand the prevailing modes of group evaporation in the spray. The next section (§ 2) describes the experimental arrangement and measurement techniques used in this study. The results are presented in § 3. The mean and fluctuating characteristics of the two phases are presented in § 3.2 and the results of the measurements of specified spatial correlations are discussed in § 3.3, together with the measured group evaporation number. A summary of the main findings can be found in § 4.
2 Experimental arrangement
The principle of combining the optical arrangements of ILIDS with PLIF has been described by Sahu et al. (Reference Sahu, Hardalupas and Taylor2014b ). They also demonstrated the application of the combined technique to two-phase measurements in an evaporating polydispersed spray. A brief summary is presented here for completeness.
The ILIDS technique is based on detecting the reflected and the first-order refracted light scattered from a droplet illuminated by a laser sheet, which, at a specific forward scattering angle, interfere to produce equally spaced parallel fringes on a defocused plane (Glover, Skippon & Boyle Reference Glover, Skippon and Boyle1995). The characteristic interferogram is observed with a far-field arrangement of receiving optics (Kawaguchi, Akasaka & Maeda Reference Kawaguchi, Akasaka and Maeda2002). The number of fringes present in each of the recorded fringe patterns is proportional to the droplet diameter. The droplet velocity is obtained by tracking the same droplet on two sequential ILIDS images, captured with a small and finite time interval. For the purpose of characterizing simultaneously vapour distribution around individual droplets using the PLIF technique, both phases are imaged on the focused plane. With this optical system, a droplet is imaged as a rectangular region with a superimposed fringe pattern on the ILIDS camera and the corresponding liquid fluorescence appears on the PLIF image, which also contains the fluorescence from droplet vapour. The droplet positions obtained through ILIDS can be used to detect the corresponding droplets on the PLIF image so that the droplet size/velocity (from ILIDS) is associated with the droplet positions on the PLIF image. The contribution of liquid fluorescence due to droplets is filtered out from the PLIF image and the resulting image is processed to obtain vapour concentration. Thus, simultaneous planar measurement of both droplet and vapour phases in evaporative sprays is achieved.
2.1 Flow and optical arrangement
Experiments are conducted with an air-assist internal mixing type nozzle (Spraying System Co. 1/4J series) producing a solid cone spray at ambient conditions, as shown in figure 1. Liquid acetone, pressurized at 1.2 bar in a pressure vessel, was fed to the nozzle through stainless steel tubes. Both air and water streams enter the injector from opposite sides, which mix within a fluid cap before being ejected from a single hole of size 1.2 mm. The flow rates of liquid acetone and air were controlled by the respective rotameters and were set to 0.03 and 15
![]() $\text{l}~\text{min}^{-1}$
, respectively. Due to the high vapour pressure of pure acetone, the liquid droplets begin to evaporate soon after injection, while interacting with the ambient air. Hence, it is simple to recreate the high evaporation rates of fuel spray without complicated heating arrangements. Also, there is no need to seed an additive into the liquid to track the vapour phase. The fluorescence signal from acetone has low dependence on the ambient pressure and temperature. This choice of fluorescent marker allows for adaptability to various operating conditions and helps to avoid the complex correction in the evaluation of the vapour concentration from the magnitude of the measured fluorescent signal (Thurber et al.
Reference Thurber, Grisch, Kirby, Votsmeier and Hanson1998). The two-phase measurements were performed 350 mm downstream of the nozzle exit (figure 1
a), which represents an axial station at around 250 times the atomizer nozzle diameter. In this way, significant evaporation has occurred and vapour–air mixing is expected to be higher than at the near nozzle region. The corresponding width of the spray at this location was approximately 100 mm. Four radial measurement locations were considered, beginning from the nozzle axis towards the outer spray at
$\text{l}~\text{min}^{-1}$
, respectively. Due to the high vapour pressure of pure acetone, the liquid droplets begin to evaporate soon after injection, while interacting with the ambient air. Hence, it is simple to recreate the high evaporation rates of fuel spray without complicated heating arrangements. Also, there is no need to seed an additive into the liquid to track the vapour phase. The fluorescence signal from acetone has low dependence on the ambient pressure and temperature. This choice of fluorescent marker allows for adaptability to various operating conditions and helps to avoid the complex correction in the evaluation of the vapour concentration from the magnitude of the measured fluorescent signal (Thurber et al.
Reference Thurber, Grisch, Kirby, Votsmeier and Hanson1998). The two-phase measurements were performed 350 mm downstream of the nozzle exit (figure 1
a), which represents an axial station at around 250 times the atomizer nozzle diameter. In this way, significant evaporation has occurred and vapour–air mixing is expected to be higher than at the near nozzle region. The corresponding width of the spray at this location was approximately 100 mm. Four radial measurement locations were considered, beginning from the nozzle axis towards the outer spray at
![]() $R=0$
, 15, 30 and 45 mm, where
$R=0$
, 15, 30 and 45 mm, where
![]() $R$
refers to the beginning of the measurement area measured from the nozzle axis. More details of the experimental arrangement can be found in Sahu (Reference Sahu2011) and Sahu et al. (Reference Sahu, Hardalupas and Taylor2014b
).
$R$
refers to the beginning of the measurement area measured from the nozzle axis. More details of the experimental arrangement can be found in Sahu (Reference Sahu2011) and Sahu et al. (Reference Sahu, Hardalupas and Taylor2014b
).

Figure 1. Schematic of the experimental arrangement and laser instrumentation: (a) elevation view and (b) plan view.
We note that we have considered alternative approaches for the injection of the liquid phase such as mono-sized droplet injection using an in-house droplet generator (Pergamalis Reference Pergamalis2002). However, such an approach has some disadvantages, as described in the following. (i) Usually, mono-disperse droplet generators tend to generate droplets with sizes much larger in comparison to the average droplet size in a typical spray for combustion applications. Such droplet sizes result in long evaporation times and the droplets must have long residence times in a flow, in order to observe a significant change of the droplet diameter due to evaporation. This means that the entrained air flow within the mono-dispersed droplet stream will dilute the small amount of vapour quickly and the interaction between air flow and droplets is limited to individual droplet evaporation. (ii) When such droplets travel over longer distances they start colliding and generating new droplet sizes. The initial narrow size range of the mono-sized droplets becomes wider at different parts of the flow and it is difficult to evaluate the origin of the droplet sizes and the contribution of the droplet evaporation to the measured droplet sizes (Orain & Hardalupas Reference Orain and Hardalupas2014). (iii) In an evaporative spray, a local vapour concentration distribution can surround larger droplets and affect the physics of evaporation. This would not be present if mono-disperse droplet streams were used. Therefore, given our past experience with various types of experiments with mono-dispersed droplet generators and after careful consideration, we decided to use a commercial atomizer which produces a polydispersed droplet size distribution that is typical to injectors used in several combustion applications, and can be quantified without evaporation, and we use this as a reference to evaluate the evolution of the evaporation rate in the spray. However, it is also noted that, earlier, droplet evaporation experiments in sprays with nearly mono-sized droplets (around
![]() $10~\unicode[STIX]{x03BC}\text{m}$
) have been reported (for instance, see Rivas & Villermaux Reference Rivas and Villermaux2016). Use of such sprays has some advantages, since it allows for well-defined boundary conditions for droplet sizes to assist comparison with spray simulations. However, this work is limited to very small droplet sizes, which follow the fluid flow turbulence fairly well, and therefore do not include effects related to the formation of droplet clusters due to interaction with flow turbulence and simultaneous variations due to droplet size. This forms the emphasis of the current research, which extends the above study to polydispersed sprays.
$10~\unicode[STIX]{x03BC}\text{m}$
) have been reported (for instance, see Rivas & Villermaux Reference Rivas and Villermaux2016). Use of such sprays has some advantages, since it allows for well-defined boundary conditions for droplet sizes to assist comparison with spray simulations. However, this work is limited to very small droplet sizes, which follow the fluid flow turbulence fairly well, and therefore do not include effects related to the formation of droplet clusters due to interaction with flow turbulence and simultaneous variations due to droplet size. This forms the emphasis of the current research, which extends the above study to polydispersed sprays.
The optical arrangement of the combined technique is shown in figure 1(b). For measurements by ILIDS, the flow field is illuminated by a frequency-doubled, double pulse Nd:YAG laser (120
![]() $\text{mJ}~\text{pulse}^{-1}$
at wavelength
$\text{mJ}~\text{pulse}^{-1}$
at wavelength
![]() $\unicode[STIX]{x1D706}=532$
nm; beam diameter 5 mm; 5 ns pulse width; New Wave Research), denoted as Laser 1. For PLIF measurement, acetone droplets and vapour were excited by a fourth harmonic generator, single-pulse Nd:YAG laser (100
$\unicode[STIX]{x1D706}=532$
nm; beam diameter 5 mm; 5 ns pulse width; New Wave Research), denoted as Laser 1. For PLIF measurement, acetone droplets and vapour were excited by a fourth harmonic generator, single-pulse Nd:YAG laser (100
![]() $\text{mJ}~\text{pulse}^{-1}$
at
$\text{mJ}~\text{pulse}^{-1}$
at
![]() $\unicode[STIX]{x1D706}=266$
nm; beam diameter 10 mm; 5 ns pulse width; Continuum), denoted as Laser 2. Using a pair of concave and convex cylindrical lenses (
$\unicode[STIX]{x1D706}=266$
nm; beam diameter 10 mm; 5 ns pulse width; Continuum), denoted as Laser 2. Using a pair of concave and convex cylindrical lenses (
![]() $f=-25$
and
$f=-25$
and
![]() $+75$
mm), the green laser beam was expanded to 15 mm in the vertical direction. Then, the two beams were combined using a beam combiner (
$+75$
mm), the green laser beam was expanded to 15 mm in the vertical direction. Then, the two beams were combined using a beam combiner (
![]() $25\times 36~\text{mm}$
; 95 % transmittance for green light and 99.9 % reflectance for UV). Utmost care was taken to ensure both beam axes were collinear and parallel to the optical bench. Both laser sheets were focused at the measurement region using a cylindrical convex lens (fused silica;
$25\times 36~\text{mm}$
; 95 % transmittance for green light and 99.9 % reflectance for UV). Utmost care was taken to ensure both beam axes were collinear and parallel to the optical bench. Both laser sheets were focused at the measurement region using a cylindrical convex lens (fused silica;
![]() $f=+400$
mm). The dimensions (height and waist) of the laser sheets at the measurement location were approximately 15 and 1 mm for
$f=+400$
mm). The dimensions (height and waist) of the laser sheets at the measurement location were approximately 15 and 1 mm for
![]() $\unicode[STIX]{x1D706}=532$
nm beam and 10 and 1 mm for the
$\unicode[STIX]{x1D706}=532$
nm beam and 10 and 1 mm for the
![]() $\unicode[STIX]{x1D706}=266$
nm beam, respectively. Acetone absorbs the UV light at 266 nm and emits fluorescence which has a spectrum in the range 350–550 nm with the peak around 435 nm, while the droplets scatter light at 532 nm without absorbing it. The wavelengths of fluorescent and scattered light are separated by using appropriate optical filters.
$\unicode[STIX]{x1D706}=266$
nm beam, respectively. Acetone absorbs the UV light at 266 nm and emits fluorescence which has a spectrum in the range 350–550 nm with the peak around 435 nm, while the droplets scatter light at 532 nm without absorbing it. The wavelengths of fluorescent and scattered light are separated by using appropriate optical filters.
The scattered light was collected through Lens 1 (135 mm; f/2.8 Nikon lens) along with a suitable band-pass optical filter (532 nm; 3 nm bandwidth) to restrict the fluorescence signal from the droplets at wavelength around 435 nm. The images were captured through Camera 1 (PCO; Sensicam QE, 12 bit,
![]() $1040\times 1376~\text{pixels}^{2}$
), set at an angle of
$1040\times 1376~\text{pixels}^{2}$
), set at an angle of
![]() $\unicode[STIX]{x1D703}=70^{\circ }$
, which is the optimum forward scattering angle for a refractive index of 1.35 (acetone in air) for sizing of acetone droplets by ILIDS with vertically polarized light. The Scheimpflug condition was maintained to ensure uniform defocusing at Camera 1. The defocusing was achieved by a pair of cylindrical lenses (
$\unicode[STIX]{x1D703}=70^{\circ }$
, which is the optimum forward scattering angle for a refractive index of 1.35 (acetone in air) for sizing of acetone droplets by ILIDS with vertically polarized light. The Scheimpflug condition was maintained to ensure uniform defocusing at Camera 1. The defocusing was achieved by a pair of cylindrical lenses (
![]() $+50$
and
$+50$
and
![]() $-50$
mm focal length). A rectangular aperture (
$-50$
mm focal length). A rectangular aperture (
![]() $4\times 40~\text{mm}^{2}$
) was placed right in front of the collecting lens of Camera 1 to adjust the collecting angle and enhance the depth of focus. The collecting angle (
$4\times 40~\text{mm}^{2}$
) was placed right in front of the collecting lens of Camera 1 to adjust the collecting angle and enhance the depth of focus. The collecting angle (
![]() $\unicode[STIX]{x1D6FC}$
) was set to
$\unicode[STIX]{x1D6FC}$
) was set to
![]() $7.15^{\circ }$
, centred around the main angle of camera orientation, resulting in resolution of 4.70
$7.15^{\circ }$
, centred around the main angle of camera orientation, resulting in resolution of 4.70
![]() $\unicode[STIX]{x03BC}\text{m}~\text{fringe}^{-1}$
for the ILIDS system. The depth of focus for the ILIDS setting was approximately 0.2 mm which is much smaller than the laser sheet thickness: however, for the ILIDS technique, the droplet images are defocused anyway. The fluorescent intensities were collected through Lens 2 (105 mm
$\unicode[STIX]{x03BC}\text{m}~\text{fringe}^{-1}$
for the ILIDS system. The depth of focus for the ILIDS setting was approximately 0.2 mm which is much smaller than the laser sheet thickness: however, for the ILIDS technique, the droplet images are defocused anyway. The fluorescent intensities were collected through Lens 2 (105 mm
![]() $f/4$
Nikon lens) with a suitable band-pass filter (260–490 nm) to restrict the scattered light from droplets at 532 nm. The lens, being made of BK7 glass, could absorb the scattered UV light at 266 nm. The fluorescent light was imaged by Camera 2 (PCO; Sensicam QE, 12 bit,
$f/4$
Nikon lens) with a suitable band-pass filter (260–490 nm) to restrict the scattered light from droplets at 532 nm. The lens, being made of BK7 glass, could absorb the scattered UV light at 266 nm. The fluorescent light was imaged by Camera 2 (PCO; Sensicam QE, 12 bit,
![]() $1040\times 1376~\text{pixels}^{2}$
), coupled to a gated intensifier (IRO image intensifier with PCO; LaVision). Because of the unavailability of a suitable Scheimpflug mount for Camera 2, the Scheimpflug condition could not be incorporated. So, Camera 2 could not be aligned at the same scattering angle
$1040\times 1376~\text{pixels}^{2}$
), coupled to a gated intensifier (IRO image intensifier with PCO; LaVision). Because of the unavailability of a suitable Scheimpflug mount for Camera 2, the Scheimpflug condition could not be incorporated. So, Camera 2 could not be aligned at the same scattering angle
![]() $\unicode[STIX]{x1D703}$
similar to Camera 1. Thus, as shown in figure 1, Camera 2 was placed at a right angle to the laser sheet, on the same side of the laser sheet as Camera 1. The depth of focus was approximately 0.9 mm for the PLIF camera setting, which is slightly less than the thickness of the laser sheet (1 mm). The lasers, cameras and intensifier were synchronously operated using LaVision DaVis software and a digital delay generator (DG 535; Stanford Research Systems). The triggering and timing of Camera 1 and Camera 2 (via the intensifier) were made synchronous with the respective laser pulses, so that the PLIF image was captured at the same time as the first of the two ILIDS images. For both cameras, the field of view was approximately
$\unicode[STIX]{x1D703}$
similar to Camera 1. Thus, as shown in figure 1, Camera 2 was placed at a right angle to the laser sheet, on the same side of the laser sheet as Camera 1. The depth of focus was approximately 0.9 mm for the PLIF camera setting, which is slightly less than the thickness of the laser sheet (1 mm). The lasers, cameras and intensifier were synchronously operated using LaVision DaVis software and a digital delay generator (DG 535; Stanford Research Systems). The triggering and timing of Camera 1 and Camera 2 (via the intensifier) were made synchronous with the respective laser pulses, so that the PLIF image was captured at the same time as the first of the two ILIDS images. For both cameras, the field of view was approximately
![]() $8\times 12~\text{mm}^{2}$
, with magnification of approximately 0.7 in both horizontal and vertical directions. For each measurement location, 2000 image pairs were captured through each of the cameras. The repetition rate of the laser was set to 5 Hz, so that the acquired images remained statistically independent.
$8\times 12~\text{mm}^{2}$
, with magnification of approximately 0.7 in both horizontal and vertical directions. For each measurement location, 2000 image pairs were captured through each of the cameras. The repetition rate of the laser was set to 5 Hz, so that the acquired images remained statistically independent.
In order to examine the effect of evaporation on droplet properties, comparison with a non-evaporative spray was essential. Hence, experiments were performed with a water spray under the same operating conditions of liquid and air flow rates, and at the same measurement locations as for the acetone spray. Although at the ambient temperature of
![]() $15\,^{\circ }\text{C}$
the surface tension of water is approximately three times greater than that of acetone, for the considered experimental regime in the spray, the droplet size can be considered to be independent of the surface tension due to the high value of Weber number at the nozzle exit.
$15\,^{\circ }\text{C}$
the surface tension of water is approximately three times greater than that of acetone, for the considered experimental regime in the spray, the droplet size can be considered to be independent of the surface tension due to the high value of Weber number at the nozzle exit.
A three-dimensional traversing frame mechanism was used to mount the whole optical assembly including the laser, laser sheet optics, cameras and lenses. This was mechanically isolated from the rig, which consists of an aluminium frame containing an air assist nozzle producing a solid cone spray. Measurements at various locations in the spray could be obtained by traversing the frame mechanism to the desired positions.
At any given measurement location, the notations ‘
![]() $x$
’ and ‘
$x$
’ and ‘
![]() $y$
’ refer to the local axial and radial directions respectively, both lying in the plane of the laser sheet. The upper-case letters denote an instantaneous quantity, while lower-case letters denote the corresponding instantaneous fluctuations from the average. For instance, instantaneous velocities in the ‘
$y$
’ refer to the local axial and radial directions respectively, both lying in the plane of the laser sheet. The upper-case letters denote an instantaneous quantity, while lower-case letters denote the corresponding instantaneous fluctuations from the average. For instance, instantaneous velocities in the ‘
![]() $x$
’ and ‘
$x$
’ and ‘
![]() $y$
’ directions are denoted by ‘
$y$
’ directions are denoted by ‘
![]() $U$
’ and ‘
$U$
’ and ‘
![]() $V$
’ and velocity fluctuations by ‘
$V$
’ and velocity fluctuations by ‘
![]() $u$
’ and ‘
$u$
’ and ‘
![]() $v$
’ respectively. Similarly, ‘
$v$
’ respectively. Similarly, ‘
![]() $Y$
’ and ‘
$Y$
’ and ‘
![]() $y$
’ refer to the instantaneous vapour mass fraction and its fluctuations, respectively. An ‘overbar’ over any quantity indicates time-averaging and the subscript ‘
$y$
’ refer to the instantaneous vapour mass fraction and its fluctuations, respectively. An ‘overbar’ over any quantity indicates time-averaging and the subscript ‘
![]() $r$
’ denotes the root mean square (r.m.s.) of that quantity.
$r$
’ denotes the root mean square (r.m.s.) of that quantity.
2.2 Image processing
The algorithm for image processing is illustrated for a pair of ILIDS and PIV images in figure 2. The details can be found in Sahu et al. (Reference Sahu, Hardalupas and Taylor2014b ).

Figure 2. Illustration of the image processing details of the combined ILIDS and PLIF technique. In the plot of simultaneous droplet size and velocity, and contours of vapour mass fraction, the circles represent droplets and the associated bold vectors represent droplet velocity. The scales for the droplet size and contour plots are different.
The image processing procedure for droplet size and velocity measurements by ILIDS is elaborated in Sahu (Reference Sahu2011). For the present case, since the scattering intensity of the vapour is much smaller than that of the droplets, the effect of the vapour was to create a low-intensity background noise on the defocused ILIDS image, which was not significant. The minimum measurable droplet size by ILIDS was 15
![]() $\unicode[STIX]{x03BC}\text{m}$
, which is obtained as a trade-off between the object distance of the collecting lens and size of the measurement area.
$\unicode[STIX]{x03BC}\text{m}$
, which is obtained as a trade-off between the object distance of the collecting lens and size of the measurement area.
The PLIF image contains fluorescence from the liquid droplets as well as the vapour phase. To suppress the high-frequency signal (noise) in the PLIF image, the intensity values were binned with a bin size of
![]() $4\times 4~\text{pixel}^{2}$
, thus resulting in a spatial resolution of
$4\times 4~\text{pixel}^{2}$
, thus resulting in a spatial resolution of
![]() $36~\unicode[STIX]{x03BC}\text{m}~\text{pixel}^{-1}$
. In order to obtain the vapour concentration from the PLIF images, first the contributions from the liquid phase had to be eliminated. For this purpose, usually a cut-off threshold based on intensity is used to distinguish the two phases. However, this approach was not suitable in the present work because the droplet size distribution was dominated by small droplets (15–20
$36~\unicode[STIX]{x03BC}\text{m}~\text{pixel}^{-1}$
. In order to obtain the vapour concentration from the PLIF images, first the contributions from the liquid phase had to be eliminated. For this purpose, usually a cut-off threshold based on intensity is used to distinguish the two phases. However, this approach was not suitable in the present work because the droplet size distribution was dominated by small droplets (15–20
![]() $\unicode[STIX]{x03BC}\text{m}$
) which caused the intensity distributions from droplets and vapour phase to overlap to a greater extent. Instead, the droplets were identified and phase discrimination was achieved by applying a one-dimensional continuous wavelet transformation (CWT) to each vertical column of the image, a method which was found to minimize cross-talk between the two phases. A circular region around the centre of each identified droplet was filtered out of the image by setting corresponding pixel intensity values to ‘zero’ (figure 2). The diameter of the circular regions was based on the negative peaks of CWT spectrum around the droplet centre. In this way the overestimation of vapour mass fraction close to droplet surface due to ‘droplet halation effect’ (Castanet et al.
Reference Castanet, Lavieille, Lebouche and Lemoine2003; Orain, Mercier & Grisch Reference Orain, Mercier and Grisch2006; Sahu et al.
Reference Sahu, Hardalupas and Taylor2014b
) could be eliminated although vapour measurement was only possible three to four droplet diameters away from the centre of a droplet. The mass loss due to masking can be in principle found by measuring the mass flow rate of liquid and vapour across the spray at the measurement location of 35 cm downstream of the injector exit and subtracting that from the inlet mass flow rate of the liquid at the injector exit. However, this is difficult to achieve due to uncertainty in the absolute value of the mass flow rate measurement from the experiment. In the ILIDS technique not all droplets in an image are validated. Hence, the measured droplet number density is lower than the actual value. The velocity of the vapour was assumed to be the same as that of the gas flow, which in turn was assumed to be equal to the velocity of the small droplets. Thus, the combined uncertainty in absolute mass flow rate measurement of liquid and vapour would obscure the estimation of small mass loss due to the masking. However, we estimated the mass loss by accounting for the average number of droplets identified on the PLIF image, the masked area around each droplet (for a given droplet the diameter of the mask was approximately four times the droplet diameter), and assuming the vapour mass fraction within the masked area corresponded to a vapour phase equal to the average vapour mass fraction. The ratio of vapour mass contained within the mask to the overall vapour mass fraction was found to be approximately 1 %.
$\unicode[STIX]{x03BC}\text{m}$
) which caused the intensity distributions from droplets and vapour phase to overlap to a greater extent. Instead, the droplets were identified and phase discrimination was achieved by applying a one-dimensional continuous wavelet transformation (CWT) to each vertical column of the image, a method which was found to minimize cross-talk between the two phases. A circular region around the centre of each identified droplet was filtered out of the image by setting corresponding pixel intensity values to ‘zero’ (figure 2). The diameter of the circular regions was based on the negative peaks of CWT spectrum around the droplet centre. In this way the overestimation of vapour mass fraction close to droplet surface due to ‘droplet halation effect’ (Castanet et al.
Reference Castanet, Lavieille, Lebouche and Lemoine2003; Orain, Mercier & Grisch Reference Orain, Mercier and Grisch2006; Sahu et al.
Reference Sahu, Hardalupas and Taylor2014b
) could be eliminated although vapour measurement was only possible three to four droplet diameters away from the centre of a droplet. The mass loss due to masking can be in principle found by measuring the mass flow rate of liquid and vapour across the spray at the measurement location of 35 cm downstream of the injector exit and subtracting that from the inlet mass flow rate of the liquid at the injector exit. However, this is difficult to achieve due to uncertainty in the absolute value of the mass flow rate measurement from the experiment. In the ILIDS technique not all droplets in an image are validated. Hence, the measured droplet number density is lower than the actual value. The velocity of the vapour was assumed to be the same as that of the gas flow, which in turn was assumed to be equal to the velocity of the small droplets. Thus, the combined uncertainty in absolute mass flow rate measurement of liquid and vapour would obscure the estimation of small mass loss due to the masking. However, we estimated the mass loss by accounting for the average number of droplets identified on the PLIF image, the masked area around each droplet (for a given droplet the diameter of the mask was approximately four times the droplet diameter), and assuming the vapour mass fraction within the masked area corresponded to a vapour phase equal to the average vapour mass fraction. The ratio of vapour mass contained within the mask to the overall vapour mass fraction was found to be approximately 1 %.
For quantitative evaluation of vapour concentration in the droplet-filtered PLIF image, the raw fluorescence images were corrected for background luminosity and variations in the laser sheet intensity profile, and finally the fluorescent intensity was converted to vapour concentration using a systematic calibration with the saturated vapour concentration (due to liquid acetone partially filled in a cuvette with its lid securely fixed at the top) corresponding to an ambient temperature of
![]() $15\,^{\circ }\text{C}$
. The acetone vapour mass fraction was computed from the vapour concentration values by assuming ideal gas behaviour of the vapour–air mixture. Since the absorption of laser energy due to droplets and vapour was low (3–15 % at different radial locations
$15\,^{\circ }\text{C}$
. The acetone vapour mass fraction was computed from the vapour concentration values by assuming ideal gas behaviour of the vapour–air mixture. Since the absorption of laser energy due to droplets and vapour was low (3–15 % at different radial locations
![]() $R=0$
to 45 mm with the larger absorption corresponding to inner radial locations) at the considered measurement locations, the corresponding corrections were not taken into account in the vapour mass fraction estimation. Also, since the fluorescence lifetime of acetone vapour is very short (around 2.4 ns) and, at atmospheric pressure, the fluorescence remains almost unaffected by quenching (Thurber & Hanson Reference Thurber and Hanson1999), the quenching correction for processing the acetone LIF images was not necessary. A similar approach has been taken earlier by other researchers, for example, Bazile & Stepowski (Reference Bazile and Stepowski1995).
$R=0$
to 45 mm with the larger absorption corresponding to inner radial locations) at the considered measurement locations, the corresponding corrections were not taken into account in the vapour mass fraction estimation. Also, since the fluorescence lifetime of acetone vapour is very short (around 2.4 ns) and, at atmospheric pressure, the fluorescence remains almost unaffected by quenching (Thurber & Hanson Reference Thurber and Hanson1999), the quenching correction for processing the acetone LIF images was not necessary. A similar approach has been taken earlier by other researchers, for example, Bazile & Stepowski (Reference Bazile and Stepowski1995).
In order to identify the same droplet on ILIDS and PLIF images, the positions of the centre of the detected droplets in both images were, respectively, projected on to the object plane (plane of laser sheet) using the calibration constants, and the right pairs of droplet fringe pattern and the corresponding droplet fluorescence were searched. For this purpose, the position of the droplet centres by ILIDS was corrected for ‘centre discrepancy’ originating because of the defocusing performed in the ILIDS technique (Hardalupas et al. Reference Hardalupas, Sahu, Taylor and Zarogoulidis2010). We adopt a method similar to Hardalupas et al. (Reference Hardalupas, Sahu, Taylor and Zarogoulidis2010) to quantify and minimize the positioning error. Finally, droplet size/velocity from ILIDS were assigned to the position of the same droplets on the PLIF image. Thus, simultaneous two-phase measurements were obtained in the evaporative spray. Figure 2 shows an example of instantaneous contour plots of acetone vapour mass fraction superimposed with size and velocity vectors of the droplets measured simultaneously with the combined techniques.
We should mention here that the droplet concentration or number density measurements in the spray were obtained using the ILIDS images. It is not possible to validate all the droplets which appear on the ILIDS image (due to the criteria imposed by image processing). However, in any instantaneous image the validation procedure of the image processing did not reject preferentially some droplet sizes. Therefore, the relative droplet number counts of different size classes remain the same compared to the case when all droplets in an image were considered. The droplet concentration was measured by counting the number of detected droplets in the ILIDS image, which correspond to a volume of
![]() $8\times 12\times 1~\text{mm}^{3}$
in the present case (thickness of the laser
$8\times 12\times 1~\text{mm}^{3}$
in the present case (thickness of the laser
![]() $\text{sheet}=1$
mm).
$\text{sheet}=1$
mm).
Before discussing the results relevant to the study of the interaction between the droplet and vapour phases, the basic statistics for each phases are presented separately for reference purposes. Some of these results are as expected, for example, radial variation of mean droplet number density, mean droplet velocity, vapour mass fraction etc., as should be the case in a flow with appropriate initial conditions. However, quantitative differences exist between the results for water and acetone sprays, radial variation of fluctuations of different quantities etc., which are not easily anticipated. Similarly, although the droplet–gas slip velocity is expected to be higher for droplets of larger size class, the probability of the normalized slip velocity quantifies the significance of the slip velocity with respect to mean droplet velocity. The identification of the presence of droplet clustering in the spray and the quantification of its magnitude based on statistical descriptions are also not easily anticipated and are not commonly considered in the numerical modelling of evaporating sprays. We have selected a typical spray that is common in many applications, including combustion, and we have characterized it in order to be able to use this information as a reference.

Figure 3. Probability of droplet size for the acetone and the water sprays at the radial locations (a)
![]() $R=0$
mm and (b)
$R=0$
mm and (b)
![]() $R=45$
mm.
$R=45$
mm.

Figure 4. (a) Comparison of probability of the three droplet size classes, and (b) variation of droplet SMD for different measurement locations for the acetone and the water sprays.
3 Results and discussion
3.1 Droplet size
Figure 3 shows the probability of the droplet size distribution at locations
![]() $R=0$
(central spray) and 45 mm (spray edge) for the acetone and the water sprays. Similar size distributions of droplets (15–100
$R=0$
(central spray) and 45 mm (spray edge) for the acetone and the water sprays. Similar size distributions of droplets (15–100
![]() $\unicode[STIX]{x03BC}\text{m}$
) were observed at the other measurement locations. The statistical analysis is presented for three different droplet size classes, namely, 15–30
$\unicode[STIX]{x03BC}\text{m}$
) were observed at the other measurement locations. The statistical analysis is presented for three different droplet size classes, namely, 15–30
![]() $\unicode[STIX]{x03BC}\text{m}$
, 30–45
$\unicode[STIX]{x03BC}\text{m}$
, 30–45
![]() $\unicode[STIX]{x03BC}\text{m}$
and 45–60
$\unicode[STIX]{x03BC}\text{m}$
and 45–60
![]() $\unicode[STIX]{x03BC}\text{m}$
. A width of each size class of
$\unicode[STIX]{x03BC}\text{m}$
. A width of each size class of
![]() $\unicode[STIX]{x0394}D=15~\unicode[STIX]{x03BC}\text{m}$
was selected as a compromise between higher statistical uncertainty (with smaller
$\unicode[STIX]{x0394}D=15~\unicode[STIX]{x03BC}\text{m}$
was selected as a compromise between higher statistical uncertainty (with smaller
![]() $\unicode[STIX]{x0394}D$
) and obtaining size-averaged information (with larger
$\unicode[STIX]{x0394}D$
) and obtaining size-averaged information (with larger
![]() $\unicode[STIX]{x0394}D$
). Figure 4(a) compares the probability of the three droplet size classes at different measurement locations for both sprays. It can be observed that the small droplets of size 15–30
$\unicode[STIX]{x0394}D$
). Figure 4(a) compares the probability of the three droplet size classes at different measurement locations for both sprays. It can be observed that the small droplets of size 15–30
![]() $\unicode[STIX]{x03BC}\text{m}$
dominate the droplet size distribution for all locations in the spray. For the water spray, the probability of 15–30
$\unicode[STIX]{x03BC}\text{m}$
dominate the droplet size distribution for all locations in the spray. For the water spray, the probability of 15–30
![]() $\unicode[STIX]{x03BC}\text{m}$
droplets increases slightly away from the spray axis due to radial transport of the smaller droplets, although the probability of other size classes remains almost invariant at different spray locations. The Sauter mean diameter (SMD) was selected as a representative diameter to evaluate the behaviour of the size distribution:
$\unicode[STIX]{x03BC}\text{m}$
droplets increases slightly away from the spray axis due to radial transport of the smaller droplets, although the probability of other size classes remains almost invariant at different spray locations. The Sauter mean diameter (SMD) was selected as a representative diameter to evaluate the behaviour of the size distribution:
 $$\begin{eqnarray}\text{SMD}=\frac{\displaystyle \mathop{\sum }_{i=1}^{n_{T}}D_{i}^{3}}{\displaystyle \mathop{\sum }_{i=1}^{n_{T}}D_{i}^{2}},\end{eqnarray}$$
$$\begin{eqnarray}\text{SMD}=\frac{\displaystyle \mathop{\sum }_{i=1}^{n_{T}}D_{i}^{3}}{\displaystyle \mathop{\sum }_{i=1}^{n_{T}}D_{i}^{2}},\end{eqnarray}$$
where ‘
![]() $D_{i}$
’ represents diameter of ‘
$D_{i}$
’ represents diameter of ‘
![]() $i$
’th identified droplet in an ILIDS image and
$i$
’th identified droplet in an ILIDS image and
![]() $n_{T}$
is the total droplet number count for all images. The SMD provides the ratio of the liquid volume over the surface area of the droplets, which is important for evaporation. Considering the accuracy of the droplet size measurement for the present case (approximately
$n_{T}$
is the total droplet number count for all images. The SMD provides the ratio of the liquid volume over the surface area of the droplets, which is important for evaporation. Considering the accuracy of the droplet size measurement for the present case (approximately
![]() $\pm 3~\unicode[STIX]{x03BC}\text{m}$
), the SMD is considered to be constant across the water spray at the measurement plane of 350 mm from the nozzle exit, as shown in figure 4(b). From figure 3(a), it can be observed that near the central location of the acetone spray, the probability of larger droplets (
$\pm 3~\unicode[STIX]{x03BC}\text{m}$
), the SMD is considered to be constant across the water spray at the measurement plane of 350 mm from the nozzle exit, as shown in figure 4(b). From figure 3(a), it can be observed that near the central location of the acetone spray, the probability of larger droplets (
![]() ${\geqslant}45~\unicode[STIX]{x03BC}\text{m}$
) is almost the same as that for water droplets and, while the probability of droplets of approximately 30
${\geqslant}45~\unicode[STIX]{x03BC}\text{m}$
) is almost the same as that for water droplets and, while the probability of droplets of approximately 30
![]() $\unicode[STIX]{x03BC}\text{m}$
reduces, more smaller droplets of approximately 20
$\unicode[STIX]{x03BC}\text{m}$
reduces, more smaller droplets of approximately 20
![]() $\unicode[STIX]{x03BC}\text{m}$
appear in comparison to the water spray. Hence, the SMDs of the two sprays are nearly same at the location
$\unicode[STIX]{x03BC}\text{m}$
appear in comparison to the water spray. Hence, the SMDs of the two sprays are nearly same at the location
![]() $R=0$
mm. However, away from the spray axis, the probability of 15–30
$R=0$
mm. However, away from the spray axis, the probability of 15–30
![]() $\unicode[STIX]{x03BC}\text{m}$
droplets increases in comparison to the water spray, while that of larger droplet size classes decreases (see figure 3
b), thus the SMD is smaller towards the edge of the spray. This is attributed to evaporation of acetone droplets since radial transport of smaller droplets away from the spray axis is not more significant in the evaporative spray owing to much smaller droplet radial velocity in comparison to the water spray.
$\unicode[STIX]{x03BC}\text{m}$
droplets increases in comparison to the water spray, while that of larger droplet size classes decreases (see figure 3
b), thus the SMD is smaller towards the edge of the spray. This is attributed to evaporation of acetone droplets since radial transport of smaller droplets away from the spray axis is not more significant in the evaporative spray owing to much smaller droplet radial velocity in comparison to the water spray.
It should be noted that comparison of SMD between acetone and water sprays is not sufficient to draw conclusions on the extent of evaporation at any measurement location. This is because, the SMD is determined by the droplet probability distribution, which may not be altered due to evaporation as, for example, droplets in the central spray region have nearly the same probability as the three droplet size classes for water and acetone sprays (figure 4 a). However, the overall reduction of SMD for the acetone spray in figure 4(b) is, as expected, caused by droplet evaporation. The extent of evaporation at any measurement location depends on two factors, namely the droplet evaporation rate and the number density of droplets. The evaporation rate of a droplet in turn depends on the droplet size, velocity and vapour mass fraction around the droplet, although the latter may be significantly influenced by the number of neighbouring droplets present. Thus, knowledge of droplet number density, droplet velocity and vapour mass fraction are also essential, and are presented below.
3.2 Mean and fluctuations of properties of droplet and vapour phases
3.2.1 Droplet number density

Figure 5. (a) Normalized mean droplet number density; (b) intensity of fluctuations of droplet number density for the three droplet size classes at different measurement locations for the acetone and the water sprays.
Figure 5(a) shows the average droplet number density,
![]() $\overline{N}$
, of the considered drop size classes at different measurement locations for both the acetone and water sprays.
$\overline{N}$
, of the considered drop size classes at different measurement locations for both the acetone and water sprays.
![]() $\overline{N}$
is normalized by the corresponding value for evaporative spray at
$\overline{N}$
is normalized by the corresponding value for evaporative spray at
![]() $R=0$
mm. The uncertainty of
$R=0$
mm. The uncertainty of
![]() $\overline{N}$
was approximately
$\overline{N}$
was approximately
![]() $\pm 4\,\%$
at a 95 % confidence interval. The average number density decreases towards the spray edge. The radial gradient of
$\pm 4\,\%$
at a 95 % confidence interval. The average number density decreases towards the spray edge. The radial gradient of
![]() $\overline{N}$
across the spray is always higher for the water spray, while evaporation reduces the gradient considerably for the acetone spray. Also, in the case of the acetone spray, due to droplet evaporation, significant reduction in the number of 15–30
$\overline{N}$
across the spray is always higher for the water spray, while evaporation reduces the gradient considerably for the acetone spray. Also, in the case of the acetone spray, due to droplet evaporation, significant reduction in the number of 15–30
![]() $\unicode[STIX]{x03BC}\text{m}$
droplets (by approximately 2–3 times) in the central spray region (
$\unicode[STIX]{x03BC}\text{m}$
droplets (by approximately 2–3 times) in the central spray region (
![]() $R=0$
mm) can be observed in comparison to the water spray. So, the vapour mass fraction is expected to be higher in this region, though the number density of droplets of other size classes reduces proportionately such that their probability remains the same for both sprays. The intensity of fluctuations of droplet number density (ratio of r.m.s. of droplet number density fluctuations to the mean value,
$R=0$
mm) can be observed in comparison to the water spray. So, the vapour mass fraction is expected to be higher in this region, though the number density of droplets of other size classes reduces proportionately such that their probability remains the same for both sprays. The intensity of fluctuations of droplet number density (ratio of r.m.s. of droplet number density fluctuations to the mean value,
![]() $n_{r}/\overline{N}$
) is shown in figure 5(b). The statistical uncertainty of
$n_{r}/\overline{N}$
) is shown in figure 5(b). The statistical uncertainty of
![]() $n_{r}$
was approximately
$n_{r}$
was approximately
![]() $\pm 9\,\%$
with 95 % confidence interval. It should be noted that for a non-evaporating spray (the water spray in the present case), the fluctuations of droplet number density are due to droplet dispersion, which can lead to preferential accumulation of droplets and formation of droplet clusters as a consequence of interaction with the carrier phase (e.g. Monchaux et al.
Reference Monchaux, Bourgoin and Cartellier2012). However, for an evaporating spray (the acetone spray) the number density fluctuations are additionally governed by droplet evaporation (i.e. the rates at which droplets of a particular intermediate size class evaporate to become smaller droplets and larger droplets evaporate to become droplets of that intermediate size class resulting in, respectively, decrease and increase in droplet number density of that intermediate size class). It can be observed in figure 5(b) that the fluctuations (relative to mean) are higher for the larger droplets, and increase towards the edge of the spray, in contrast to trends in variations of the mean values (figure 5
a). Also, importantly, evaporation causes increased fluctuations of droplet number density at all measurement locations within the spray. Near the spray edge these fluctuations can even be higher than their corresponding mean values.
$\pm 9\,\%$
with 95 % confidence interval. It should be noted that for a non-evaporating spray (the water spray in the present case), the fluctuations of droplet number density are due to droplet dispersion, which can lead to preferential accumulation of droplets and formation of droplet clusters as a consequence of interaction with the carrier phase (e.g. Monchaux et al.
Reference Monchaux, Bourgoin and Cartellier2012). However, for an evaporating spray (the acetone spray) the number density fluctuations are additionally governed by droplet evaporation (i.e. the rates at which droplets of a particular intermediate size class evaporate to become smaller droplets and larger droplets evaporate to become droplets of that intermediate size class resulting in, respectively, decrease and increase in droplet number density of that intermediate size class). It can be observed in figure 5(b) that the fluctuations (relative to mean) are higher for the larger droplets, and increase towards the edge of the spray, in contrast to trends in variations of the mean values (figure 5
a). Also, importantly, evaporation causes increased fluctuations of droplet number density at all measurement locations within the spray. Near the spray edge these fluctuations can even be higher than their corresponding mean values.
3.2.2 Droplet velocity
Figure 6 shows the vector plots of the average droplet velocity of 15–30
![]() $\unicode[STIX]{x03BC}\text{m}$
droplets for the acetone spray, which indicate that the droplet velocity is mostly axial and with a downward direction (away from the nozzle), and its magnitude decreases away from the spray centre. The mean droplet velocity is observed to be almost spatially invariant within each measurement region. The same is true for droplet velocity fluctuations. Similar trends were observed for water droplets, so are not presented here. For the reason mentioned above, the spatially averaged velocity of droplets (of any size class) across each measurement area (i.e.
$\unicode[STIX]{x03BC}\text{m}$
droplets for the acetone spray, which indicate that the droplet velocity is mostly axial and with a downward direction (away from the nozzle), and its magnitude decreases away from the spray centre. The mean droplet velocity is observed to be almost spatially invariant within each measurement region. The same is true for droplet velocity fluctuations. Similar trends were observed for water droplets, so are not presented here. For the reason mentioned above, the spatially averaged velocity of droplets (of any size class) across each measurement area (i.e.
![]() $8\times 12~\text{mm}^{2}$
) is considered to be representative of individual droplet velocity of that size class. Figure 7(a,b) compares respectively the spatially averaged mean axial velocity (
$8\times 12~\text{mm}^{2}$
) is considered to be representative of individual droplet velocity of that size class. Figure 7(a,b) compares respectively the spatially averaged mean axial velocity (
![]() $\overline{U}$
) and intensity of axial velocity fluctuations (
$\overline{U}$
) and intensity of axial velocity fluctuations (
![]() $u_{r}/\overline{U}$
) for droplets of the considered size class for acetone and water sprays. The uncertainties (with 95 % confidence interval) of
$u_{r}/\overline{U}$
) for droplets of the considered size class for acetone and water sprays. The uncertainties (with 95 % confidence interval) of
![]() $\overline{U}$
and
$\overline{U}$
and
![]() $u_{r}$
were approximately
$u_{r}$
were approximately
![]() $\pm 1\,\%$
and
$\pm 1\,\%$
and
![]() $\pm 15\,\%$
respectively. Although no significant difference is present in the mean velocity between the droplet size classes, the droplet velocity is consistently higher for larger droplet size classes. It is observed that evaporation caused the mean and fluctuations of droplet velocity to become more uniform across the spray radial profile. This requires some explanation, which is provided below.
$\pm 15\,\%$
respectively. Although no significant difference is present in the mean velocity between the droplet size classes, the droplet velocity is consistently higher for larger droplet size classes. It is observed that evaporation caused the mean and fluctuations of droplet velocity to become more uniform across the spray radial profile. This requires some explanation, which is provided below.

Figure 6. Vector plots of mean droplet velocity for acetone droplets of size class of 15–30
![]() $\unicode[STIX]{x03BC}\text{m}$
at different measurement locations.
$\unicode[STIX]{x03BC}\text{m}$
at different measurement locations.

Figure 7. (a) Mean droplet velocity and (b) intensity of fluctuations of droplet velocity at different measurement locations for acetone and water droplets for the three droplet size classes.
In comparison to the water droplets, the mean velocity of acetone droplets appears to be smaller near the spray axis and higher towards the spray edge (by approximately 10 %). However, it can be shown to a first approximation that evaporation is expected to always cause reduction of droplet velocity. From (1.4), the rate of change of size of a droplet can be expressed as
Since the droplet Reynolds number (based on its mean velocity) is low (
![]() ${\approx}0.2$
), assuming Stokes’ drag law for a single droplet, and considering the effect of evaporation on droplet drag (Spalding Reference Spalding1951),
${\approx}0.2$
), assuming Stokes’ drag law for a single droplet, and considering the effect of evaporation on droplet drag (Spalding Reference Spalding1951),
From the above equations it can be shown that
Assuming that for a given measurement location the transfer number
![]() $B$
and the gas velocity
$B$
and the gas velocity
![]() $U_{g}$
are constants within the measurement volume, and since
$U_{g}$
are constants within the measurement volume, and since
![]() $Sh\rightarrow 2$
as
$Sh\rightarrow 2$
as
![]() $Re\rightarrow 0$
, integration of the above equation implies that droplet velocity reduces proportionately with droplet size. We consider the droplet size range of 15–30
$Re\rightarrow 0$
, integration of the above equation implies that droplet velocity reduces proportionately with droplet size. We consider the droplet size range of 15–30
![]() $\unicode[STIX]{x03BC}\text{m}$
as an example to explain the trends of figure 7(a). For the location at
$\unicode[STIX]{x03BC}\text{m}$
as an example to explain the trends of figure 7(a). For the location at
![]() $R=0$
mm, the velocity of 15–30
$R=0$
mm, the velocity of 15–30
![]() $\unicode[STIX]{x03BC}\text{m}$
acetone droplets, which before evaporation had a larger size (say 30–45
$\unicode[STIX]{x03BC}\text{m}$
acetone droplets, which before evaporation had a larger size (say 30–45
![]() $\unicode[STIX]{x03BC}\text{m}$
; this droplet size range is selected only to demonstrate our argument) with a larger velocity, is now smaller compared to water droplets of the same size. Equation (3.4) also shows that the rate
$\unicode[STIX]{x03BC}\text{m}$
; this droplet size range is selected only to demonstrate our argument) with a larger velocity, is now smaller compared to water droplets of the same size. Equation (3.4) also shows that the rate
![]() $\text{d}U/\text{d}D$
is smaller for larger
$\text{d}U/\text{d}D$
is smaller for larger
![]() $B$
. Since
$B$
. Since
![]() $B$
increases towards the spray edge (as the vapour mass fraction away from a droplet is smaller), the evaporation rate (
$B$
increases towards the spray edge (as the vapour mass fraction away from a droplet is smaller), the evaporation rate (
![]() $\text{d}D/\text{d}t$
) is higher but
$\text{d}D/\text{d}t$
) is higher but
![]() $\text{d}U/\text{d}D$
is smaller. Thus, for the location at
$\text{d}U/\text{d}D$
is smaller. Thus, for the location at
![]() $R=45$
mm, the velocity of 15–30
$R=45$
mm, the velocity of 15–30
![]() $\unicode[STIX]{x03BC}\text{m}$
acetone droplets, which used to be of even larger size (say 45–60
$\unicode[STIX]{x03BC}\text{m}$
acetone droplets, which used to be of even larger size (say 45–60
![]() $\unicode[STIX]{x03BC}\text{m}$
; again this droplet size range is selected only to demonstrate our argument) with an even larger velocity, is now larger compared to water droplets of the same size. The above discussion does not consider the response of the different droplet sizes to the induced mean airflow in the spray, which will be discussed below.
$\unicode[STIX]{x03BC}\text{m}$
; again this droplet size range is selected only to demonstrate our argument) with an even larger velocity, is now larger compared to water droplets of the same size. The above discussion does not consider the response of the different droplet sizes to the induced mean airflow in the spray, which will be discussed below.
For both sprays, the axial velocity fluctuations were smaller than the respective mean values at all measurement locations although they increased away from the spray centre, and were smaller for larger droplet size classes (figure 7
b). Also, fluctuations of droplet velocity were higher for the acetone droplets compared to water droplets for both axial directions (approximately 15 %) and radial direction (approximately 25 %). The anisotropy of the droplet velocity fluctuations, defined as the ratio of
![]() $u_{r}/v_{r}$
, was approximately 1.5–2 for all cases, and was slightly reduced away from the spray axis. These characteristics are according to expectations for a jet flow, which is approximately the flow behaviour induced by the spray.
$u_{r}/v_{r}$
, was approximately 1.5–2 for all cases, and was slightly reduced away from the spray axis. These characteristics are according to expectations for a jet flow, which is approximately the flow behaviour induced by the spray.

Figure 8. Probability of instantaneous droplet–gas slip velocity in the axial direction for 30–45
![]() $\unicode[STIX]{x03BC}\text{m}$
and 45–60
$\unicode[STIX]{x03BC}\text{m}$
and 45–60
![]() $\unicode[STIX]{x03BC}\text{m}$
droplet size classes for the acetone spray at the measurement location
$\unicode[STIX]{x03BC}\text{m}$
droplet size classes for the acetone spray at the measurement location
![]() $R=0$
mm.
$R=0$
mm.
The droplet–gas slip velocity is an important parameter, which not only influences droplet evaporation and drag (equations (3.2) and (3.3)) but also the correspondence between droplet properties and neighbouring vapour mass fraction. Therefore, the droplet slip velocity was determined by considering the instantaneous relative velocity of droplets with respect to gas velocity (approximated by the velocity of 15–30
![]() $\unicode[STIX]{x03BC}\text{m}$
droplets, which is justified by the Stokes number evaluation presented below) for the evaporative spray. The corresponding probability distributions for the 30–45
$\unicode[STIX]{x03BC}\text{m}$
droplets, which is justified by the Stokes number evaluation presented below) for the evaporative spray. The corresponding probability distributions for the 30–45
![]() $\unicode[STIX]{x03BC}\text{m}$
and 45–60
$\unicode[STIX]{x03BC}\text{m}$
and 45–60
![]() $\unicode[STIX]{x03BC}\text{m}$
droplet size classes are shown in figure 8 for the axial velocity component of the droplets. The slip velocity for a given droplet size class is normalized by the respective mean velocity of the droplet size class. It is observed that the mean droplet–gas slip velocity is close to zero, thus the droplet Reynolds number for droplets of all sizes is very small (
$\unicode[STIX]{x03BC}\text{m}$
droplet size classes are shown in figure 8 for the axial velocity component of the droplets. The slip velocity for a given droplet size class is normalized by the respective mean velocity of the droplet size class. It is observed that the mean droplet–gas slip velocity is close to zero, thus the droplet Reynolds number for droplets of all sizes is very small (
![]() $Re<1$
). However, the slip velocity of the droplets has both positive and negative sign, indicating that droplets may lead or lag the gas motion. This refers to fluctuations of slip velocity indicating the role of gas-phase turbulence. Therefore, the vapour evacuation due to convective effects (mean slip) is not expected to be significant in comparison to the turbulence effects. This highlights the differences in the droplet evaporation experiments based on isolated pendant droplets (typically in wind tunnels), where the convective effects are always dominant, and sprays. Nevertheless, as will be explained later, the instantaneous slip velocity is responsible for spatial disparity between the locations of droplets and vapour, which results in reduced correlation between the two phases.
$Re<1$
). However, the slip velocity of the droplets has both positive and negative sign, indicating that droplets may lead or lag the gas motion. This refers to fluctuations of slip velocity indicating the role of gas-phase turbulence. Therefore, the vapour evacuation due to convective effects (mean slip) is not expected to be significant in comparison to the turbulence effects. This highlights the differences in the droplet evaporation experiments based on isolated pendant droplets (typically in wind tunnels), where the convective effects are always dominant, and sprays. Nevertheless, as will be explained later, the instantaneous slip velocity is responsible for spatial disparity between the locations of droplets and vapour, which results in reduced correlation between the two phases.
Table 1. Estimated turbulent characteristics of the air flow in the acetone spray and corresponding droplet Stokes numbers for the 15–30
![]() $\unicode[STIX]{x03BC}\text{m}$
, 30–45
$\unicode[STIX]{x03BC}\text{m}$
, 30–45
![]() $\unicode[STIX]{x03BC}\text{m}$
and 45–60
$\unicode[STIX]{x03BC}\text{m}$
and 45–60
![]() $\unicode[STIX]{x03BC}\text{m}$
droplet size classes at the measurement locations
$\unicode[STIX]{x03BC}\text{m}$
droplet size classes at the measurement locations
![]() $R=0$
and 45 mm.
$R=0$
and 45 mm.

Table 1 shows the estimated turbulent characteristics of the air flow for the acetone spray at measurement locations
![]() $R=0$
mm and 45 mm. Since the air velocity around the droplets was not measured in our experiments, the gas velocity is assumed to be the same as the velocity of small droplets of size 15–30
$R=0$
mm and 45 mm. Since the air velocity around the droplets was not measured in our experiments, the gas velocity is assumed to be the same as the velocity of small droplets of size 15–30
![]() $\unicode[STIX]{x03BC}\text{m}$
. These droplets are expected to faithfully follow the gas flow since the measurement location is situated far downstream of the injector exit, and so the ‘ballistic’ motion of atomized droplets that strongly determines droplet motion near the atomizer (Hardalupas et al.
Reference Hardalupas, Taylor and Whitelaw1990) is attenuated. This is supported by the Stokes number analysis presented below. The integral length scale (
$\unicode[STIX]{x03BC}\text{m}$
. These droplets are expected to faithfully follow the gas flow since the measurement location is situated far downstream of the injector exit, and so the ‘ballistic’ motion of atomized droplets that strongly determines droplet motion near the atomizer (Hardalupas et al.
Reference Hardalupas, Taylor and Whitelaw1990) is attenuated. This is supported by the Stokes number analysis presented below. The integral length scale (
![]() $L$
) of the turbulent air flow is determined by measuring spatial velocity correlation coefficients between fluctuations of velocity of 15–35
$L$
) of the turbulent air flow is determined by measuring spatial velocity correlation coefficients between fluctuations of velocity of 15–35
![]() $\unicode[STIX]{x03BC}\text{m}$
droplets following the method described in Sahu et al. (Reference Sahu, Hardalupas and Taylor2014a
). The value of
$\unicode[STIX]{x03BC}\text{m}$
droplets following the method described in Sahu et al. (Reference Sahu, Hardalupas and Taylor2014a
). The value of
![]() $L$
at
$L$
at
![]() $R=0$
mm is approximately 13 mm, which is in agreement with the value of
$R=0$
mm is approximately 13 mm, which is in agreement with the value of
![]() $L$
estimated as
$L$
estimated as
![]() $1/5$
of the spray radius (
$1/5$
of the spray radius (
![]() ${\approx}10$
mm), as suggested by Tennekes & Lumley (Reference Tennekes and Lumley1972). The characteristic time scale of the entrained air flow by the spray (
${\approx}10$
mm), as suggested by Tennekes & Lumley (Reference Tennekes and Lumley1972). The characteristic time scale of the entrained air flow by the spray (
![]() $\unicode[STIX]{x1D70F}_{g}$
) is chosen as the ratio of the integral length scale to the axial r.m.s. velocity of the 15–30
$\unicode[STIX]{x1D70F}_{g}$
) is chosen as the ratio of the integral length scale to the axial r.m.s. velocity of the 15–30
![]() $\unicode[STIX]{x03BC}\text{m}$
droplets. The Stokes number (
$\unicode[STIX]{x03BC}\text{m}$
droplets. The Stokes number (
![]() $St$
) of a droplet size class is defined as the ratio of the droplet aerodynamic time constant or the ‘droplet relaxation time’ (
$St$
) of a droplet size class is defined as the ratio of the droplet aerodynamic time constant or the ‘droplet relaxation time’ (
![]() $\unicode[STIX]{x1D70F}_{d}$
) to an appropriate turbulence time scale of the flow. Based on the characteristic time of the entrained air flow by the spray, the Stokes number of the 15–30
$\unicode[STIX]{x1D70F}_{d}$
) to an appropriate turbulence time scale of the flow. Based on the characteristic time of the entrained air flow by the spray, the Stokes number of the 15–30
![]() $\unicode[STIX]{x03BC}\text{m}$
, 30–45
$\unicode[STIX]{x03BC}\text{m}$
, 30–45
![]() $\unicode[STIX]{x03BC}\text{m}$
and 45–60
$\unicode[STIX]{x03BC}\text{m}$
and 45–60
![]() $\unicode[STIX]{x03BC}\text{m}$
droplet size classes at the spray centre are estimated as
$\unicode[STIX]{x03BC}\text{m}$
droplet size classes at the spray centre are estimated as
![]() $St_{L}=0.05$
, 0.16 and 0.30, respectively. This means that while droplets of 15–30
$St_{L}=0.05$
, 0.16 and 0.30, respectively. This means that while droplets of 15–30
![]() $\unicode[STIX]{x03BC}\text{m}$
follow the gas motion, larger droplets show partial response to the large-scale eddies of the gas phase. The estimated values in table 1 were nearly the same for the water spray, hence are not presented here.
$\unicode[STIX]{x03BC}\text{m}$
follow the gas motion, larger droplets show partial response to the large-scale eddies of the gas phase. The estimated values in table 1 were nearly the same for the water spray, hence are not presented here.
Since the estimated
![]() $St_{L}$
for the smallest droplet size class is very low (
$St_{L}$
for the smallest droplet size class is very low (
![]() $=$
0.05), this justifies our assumption of those droplets following the air flow faithfully. Also, the fact that the droplet–gas slip velocity decreases significantly for all droplet sizes far downstream of the injector exit (see Gounder, Kourmatzis & Masri Reference Gounder, Kourmatzis and Masri2012; Sahu et al.
Reference Sahu, Hardalupas and Taylor2016) further supports the above assumption. However, in our earlier work (Sahu et al.
Reference Sahu, Hardalupas and Taylor2014a
) we have shown that the integral length scale of the droplet flow is smaller than that of the gas flow, and also, the gas velocity fluctuations are smaller than the droplet velocity fluctuations, though the differences are smaller for droplets of low Stokes number. Thus, the energy-containing eddy time scale is expected to be slightly overestimated, and the Stokes numbers are expected to be smaller than the estimated values presented in table 1. Nevertheless, we emphasize that the turbulent characteristics and Stokes numbers are good estimates in an order of magnitude sense.
$=$
0.05), this justifies our assumption of those droplets following the air flow faithfully. Also, the fact that the droplet–gas slip velocity decreases significantly for all droplet sizes far downstream of the injector exit (see Gounder, Kourmatzis & Masri Reference Gounder, Kourmatzis and Masri2012; Sahu et al.
Reference Sahu, Hardalupas and Taylor2016) further supports the above assumption. However, in our earlier work (Sahu et al.
Reference Sahu, Hardalupas and Taylor2014a
) we have shown that the integral length scale of the droplet flow is smaller than that of the gas flow, and also, the gas velocity fluctuations are smaller than the droplet velocity fluctuations, though the differences are smaller for droplets of low Stokes number. Thus, the energy-containing eddy time scale is expected to be slightly overestimated, and the Stokes numbers are expected to be smaller than the estimated values presented in table 1. Nevertheless, we emphasize that the turbulent characteristics and Stokes numbers are good estimates in an order of magnitude sense.
3.2.3 Vapour mass fraction
The contour plots of average vapour mass fraction (
![]() $\overline{Y}$
) are presented in figure 9. As compared to the saturated condition (
$\overline{Y}$
) are presented in figure 9. As compared to the saturated condition (
![]() $Y_{sat}=0.32$
at
$Y_{sat}=0.32$
at
![]() $15\,^{\circ }\text{C}$
), the mean vapour mass fraction was low (
$15\,^{\circ }\text{C}$
), the mean vapour mass fraction was low (
![]() ${\approx}5$
–15 % of the saturation value) throughout the measurement region. This corresponds to equivalence ratio of approximately 0.07–0.3 implying a lean mixture. Also, as expected,
${\approx}5$
–15 % of the saturation value) throughout the measurement region. This corresponds to equivalence ratio of approximately 0.07–0.3 implying a lean mixture. Also, as expected,
![]() $\overline{Y}$
reduces considerably for measurement locations towards the edge of the spray in accordance with the reduction of acetone droplet number density (compared to the water droplets), as presented in figure 5(a). This confirms that the assumption of neglecting laser energy absorption by the vapour in the vapour mass fraction evaluation from the PLIF measurements is valid. In general,
$\overline{Y}$
reduces considerably for measurement locations towards the edge of the spray in accordance with the reduction of acetone droplet number density (compared to the water droplets), as presented in figure 5(a). This confirms that the assumption of neglecting laser energy absorption by the vapour in the vapour mass fraction evaluation from the PLIF measurements is valid. In general,
![]() $\overline{Y}$
is expected to increase in the direction of mean flow downstream as the droplets continue to release vapour during their motion away from the nozzle exit. However, this effect is expected not to be significant in the present case, since the droplet evaporation time,
$\overline{Y}$
is expected to increase in the direction of mean flow downstream as the droplets continue to release vapour during their motion away from the nozzle exit. However, this effect is expected not to be significant in the present case, since the droplet evaporation time,
![]() $\unicode[STIX]{x1D70F}_{v}\approx 50$
–40 ms (obtained from (3.2) and based on droplet SMD, as explained later), is larger than the droplet residence time within the measurement window (
$\unicode[STIX]{x1D70F}_{v}\approx 50$
–40 ms (obtained from (3.2) and based on droplet SMD, as explained later), is larger than the droplet residence time within the measurement window (
![]() ${\approx}5$
–10 ms), where the limits of the time interval correspond to the spray centre and edge, respectively.
${\approx}5$
–10 ms), where the limits of the time interval correspond to the spray centre and edge, respectively.

Figure 9. Contour plots of mean mass fraction of acetone vapour at different measurement locations:
![]() $R$
$R$
![]() $=$
0 mm (a), 15 mm (b), 30 mm (c) and 45 mm (d) for the acetone spray.
$=$
0 mm (a), 15 mm (b), 30 mm (c) and 45 mm (d) for the acetone spray.

Figure 10. Radial profiles of (a) mean vapour mass fraction and (b) intensity of fluctuations of vapour mass fraction in the acetone spray.
For the rest of the paper, the spatial average of the vapour mass fraction within the measurement area of
![]() $8\times 12~\text{mm}^{2}$
across an ‘instantaneous’ realization is considered to be representative of the vapour mass fraction at that instant. This is done to allow estimation of the correlation between instantaneous vapour mass fraction, and droplet number density and velocity, which will be presented later. Also, this is justified since no notable spatial gradient of vapour concentration is observed in figure 9 for either axial or radial directions at each of the measurement locations. The average values of the instantaneous vapour mass fraction over all realizations is obtained and presented in figure 10 along with the corresponding normalized fluctuations of vapour mass fraction (
$8\times 12~\text{mm}^{2}$
across an ‘instantaneous’ realization is considered to be representative of the vapour mass fraction at that instant. This is done to allow estimation of the correlation between instantaneous vapour mass fraction, and droplet number density and velocity, which will be presented later. Also, this is justified since no notable spatial gradient of vapour concentration is observed in figure 9 for either axial or radial directions at each of the measurement locations. The average values of the instantaneous vapour mass fraction over all realizations is obtained and presented in figure 10 along with the corresponding normalized fluctuations of vapour mass fraction (
![]() $y_{r}/\overline{Y}$
). This is consistent with figure 9 and, as expected, the mean vapour mass fraction reduces away from the spray axis. However, the fluctuations (relative to the mean) increase away from the spray axis, as a consequence of the local fluctuations of droplet number density and velocity for which similar trends were observed (figure 5
b). In fact, near the spray boundary, the fluctuations of vapour mass fraction are of the same order as the mean value.
$y_{r}/\overline{Y}$
). This is consistent with figure 9 and, as expected, the mean vapour mass fraction reduces away from the spray axis. However, the fluctuations (relative to the mean) increase away from the spray axis, as a consequence of the local fluctuations of droplet number density and velocity for which similar trends were observed (figure 5
b). In fact, near the spray boundary, the fluctuations of vapour mass fraction are of the same order as the mean value.
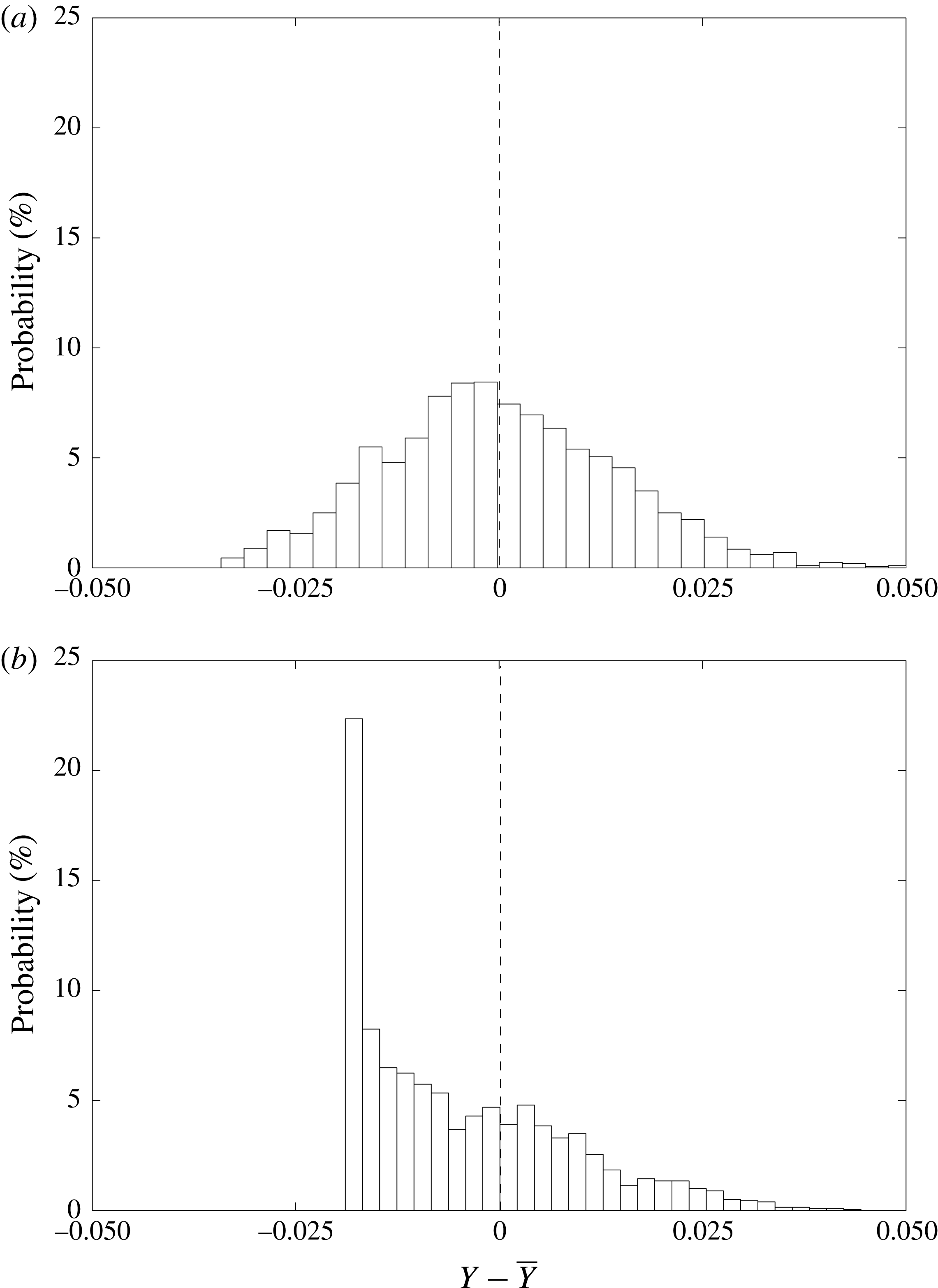
Figure 11. Probability distribution of fluctuations of vapour mass fraction at
![]() $R=0$
mm (a) and 45 mm (b).
$R=0$
mm (a) and 45 mm (b).
Figure 11 presents the probability distributions of the instantaneous vapour mass fraction within the acetone spray at the measurement locations
![]() $R=0$
mm and 45 mm respectively. These probability distributions signify temporal variations of vapour mass fraction around the droplets, hence the transfer number
$R=0$
mm and 45 mm respectively. These probability distributions signify temporal variations of vapour mass fraction around the droplets, hence the transfer number
![]() $B$
is expected also to be a time-varying parameter and therefore may not be assumed constant. While at the spray centre, the probability distribution function of the vapour mass fraction is approximately Gaussian, near the spray edge the probability function is positively skewed with a peak appearing at the minimum vapour mass fraction values (figure 11
b). This can be explained as follows. For measurement locations close to the spray edge (
$B$
is expected also to be a time-varying parameter and therefore may not be assumed constant. While at the spray centre, the probability distribution function of the vapour mass fraction is approximately Gaussian, near the spray edge the probability function is positively skewed with a peak appearing at the minimum vapour mass fraction values (figure 11
b). This can be explained as follows. For measurement locations close to the spray edge (
![]() $R=30$
and 45 mm), an instantaneous PLIF image may not contain any droplets. The vapour mass fraction in such cases was found to be very low and can be either due to vapour transported from elsewhere or background noise (even though a background noise image is subtracted from the measured LIF intensity, some shot-to-shot variation of laser energy is possible). Thus, the peak probability, corresponding to nearly zero vapour mass fraction, is attributed to the flow intermittency near the spray edge.
$R=30$
and 45 mm), an instantaneous PLIF image may not contain any droplets. The vapour mass fraction in such cases was found to be very low and can be either due to vapour transported from elsewhere or background noise (even though a background noise image is subtracted from the measured LIF intensity, some shot-to-shot variation of laser energy is possible). Thus, the peak probability, corresponding to nearly zero vapour mass fraction, is attributed to the flow intermittency near the spray edge.
3.3 Quantification of interaction between droplet and vapour phases
3.3.1 Correlation between droplet number density and vapour mass fraction
At first sight, it may appear that the momentum and inertia of the droplets can easily separate them from the vapour that they release due to evaporation, so that the measured droplets at any location in the flow are not responsible for the local vapour. However, it is important to note that the correlation between droplet and surrounding vapour depends on the droplet evaporation rate as well as the droplet Stokes number
![]() $St$
(in other words how well the droplets follow the surrounding gas flow) and density difference between the vapour and ambient gas. Although the density of acetone vapour is nearly twice that of the air, due to the very low vapour mass fraction (figure 9) the mixture density can be assumed to be the same as that of the air. For our experimental conditions, as mentioned before,
$St$
(in other words how well the droplets follow the surrounding gas flow) and density difference between the vapour and ambient gas. Although the density of acetone vapour is nearly twice that of the air, due to the very low vapour mass fraction (figure 9) the mixture density can be assumed to be the same as that of the air. For our experimental conditions, as mentioned before,
![]() $St_{L}\approx 0.1$
, which means medium and large droplet sizes partially follow the large scales of the air flow. This means the generated vapour is transported with the droplets. Hence, a certain level of correspondence between local droplets and surrounding vapour mass fraction is expected. This is confirmed in figure 12, which presents the scatter plot of the instantaneous droplet number density (
$St_{L}\approx 0.1$
, which means medium and large droplet sizes partially follow the large scales of the air flow. This means the generated vapour is transported with the droplets. Hence, a certain level of correspondence between local droplets and surrounding vapour mass fraction is expected. This is confirmed in figure 12, which presents the scatter plot of the instantaneous droplet number density (
![]() $N$
), measured by ILIDS, and the corresponding local vapour mass fraction, (
$N$
), measured by ILIDS, and the corresponding local vapour mass fraction, (
![]() $Y$
) measured by PLIF, for measurement locations at
$Y$
) measured by PLIF, for measurement locations at
![]() $R=0$
mm and 45 mm. The plots signify proportionate increase of acetone vapour (within the measurement region) with droplet number density in an average sense (as shown by the linear fit of the data). This linear dependence of the two quantities is expected if the droplets are far apart from each other, so that the total generated vapour is simply a multiple of the vapour released by single droplets: these characteristics indicate the relevance of the
$R=0$
mm and 45 mm. The plots signify proportionate increase of acetone vapour (within the measurement region) with droplet number density in an average sense (as shown by the linear fit of the data). This linear dependence of the two quantities is expected if the droplets are far apart from each other, so that the total generated vapour is simply a multiple of the vapour released by single droplets: these characteristics indicate the relevance of the
![]() $d^{2}$
-law for the modelling of droplet evaporation. However, considerable scatter is observed around the linear dependence of figure 12 for both number density
$d^{2}$
-law for the modelling of droplet evaporation. However, considerable scatter is observed around the linear dependence of figure 12 for both number density
![]() $N$
and vapour mass fraction
$N$
and vapour mass fraction
![]() $Y$
axes. The spreading along the
$Y$
axes. The spreading along the
![]() $N$
-axis (horizontal) indicates the presence of the same amount of vapour for different droplet numbers in the measurement region, while the spreading in the
$N$
-axis (horizontal) indicates the presence of the same amount of vapour for different droplet numbers in the measurement region, while the spreading in the
![]() $Y$
-axis (vertical) indicates variation of vapour mass fraction for the same number of droplets present in the measurement region. This can be attributed to dispersion of droplets due to interaction with carrier-phase turbulent flow, which leads to droplet clustering resulting in smaller inter-droplet spacing than the average, which consequently reduces the droplet evaporation rate which is then determined by the group evaporation of droplet clouds. On the other hand, scalar mixing of droplet vapour with the surrounding air results in local dissipation of vapour fluctuations. Hence, the scattering of the data can be attributed to competition between droplet dispersion and scalar mixing. It can also be observed in figure 12 that the extent of spreading for both
$Y$
-axis (vertical) indicates variation of vapour mass fraction for the same number of droplets present in the measurement region. This can be attributed to dispersion of droplets due to interaction with carrier-phase turbulent flow, which leads to droplet clustering resulting in smaller inter-droplet spacing than the average, which consequently reduces the droplet evaporation rate which is then determined by the group evaporation of droplet clouds. On the other hand, scalar mixing of droplet vapour with the surrounding air results in local dissipation of vapour fluctuations. Hence, the scattering of the data can be attributed to competition between droplet dispersion and scalar mixing. It can also be observed in figure 12 that the extent of spreading for both
![]() $N$
and
$N$
and
![]() $Y$
directions is reduced for the case of location
$Y$
directions is reduced for the case of location
![]() $R=45$
mm in comparison to the central spray location, and the slope of the linear fit is larger. This indicates that the group evaporation tendency of droplets reduces towards the spray boundary. It should be noted that the dependence between
$R=45$
mm in comparison to the central spray location, and the slope of the linear fit is larger. This indicates that the group evaporation tendency of droplets reduces towards the spray boundary. It should be noted that the dependence between
![]() $N$
and
$N$
and
![]() $Y$
, as presented above, is important for the evaluation of the Eulerian joint probability density function of mixture fraction and vapour source term, which can fully describe the unclosed source terms appearing in the transport equations of mixture fraction in (1.1) and (1.2) (Reveillon & Vervisch Reference Reveillon and Vervisch2000). Experimental evaluation of these terms is not available in the literature.
$Y$
, as presented above, is important for the evaluation of the Eulerian joint probability density function of mixture fraction and vapour source term, which can fully describe the unclosed source terms appearing in the transport equations of mixture fraction in (1.1) and (1.2) (Reveillon & Vervisch Reference Reveillon and Vervisch2000). Experimental evaluation of these terms is not available in the literature.

Figure 12. Scatter plot of instantaneous droplet number density and vapour mass fraction at
![]() $R=0$
mm (a) and 45 mm (b).
$R=0$
mm (a) and 45 mm (b).
The above discussion explained the need to evaluate the correlation between fluctuations of droplet number densities and vapour mass fraction
![]() $\overline{n\times y}$
from our measurements, which uniquely provides this ability. Since the definition of the mixture fraction in sprays (containing vapour sources) is not straightforward (Reveillon & Vervisch Reference Reveillon and Vervisch2000), we present
$\overline{n\times y}$
from our measurements, which uniquely provides this ability. Since the definition of the mixture fraction in sprays (containing vapour sources) is not straightforward (Reveillon & Vervisch Reference Reveillon and Vervisch2000), we present
![]() $\overline{n\times y}$
. The corresponding correlation coefficient, denoted as
$\overline{n\times y}$
. The corresponding correlation coefficient, denoted as
![]() $R_{n\ast y}$
, can be expressed for droplet size class
$R_{n\ast y}$
, can be expressed for droplet size class
![]() $D$
as
$D$
as
where
![]() $n_{r}$
and
$n_{r}$
and
![]() $y_{r}$
are the r.m.s. of the number density fluctuations for size class
$y_{r}$
are the r.m.s. of the number density fluctuations for size class
![]() $D$
and mass fraction fluctuations respectively.
$D$
and mass fraction fluctuations respectively.
![]() $R_{n\ast y}$
, evaluated for each droplet size class and for different measurement locations in the acetone spray, is presented in figure 13. The uncertainty in
$R_{n\ast y}$
, evaluated for each droplet size class and for different measurement locations in the acetone spray, is presented in figure 13. The uncertainty in
![]() $R_{n\ast y}$
was approximately
$R_{n\ast y}$
was approximately
![]() $\pm 0.05$
with 95 % confidence interval.
$\pm 0.05$
with 95 % confidence interval.

Figure 13. Correlation coefficient (
![]() $R_{n\ast y}$
) between fluctuations of number density (for different droplet size classes) and vapour mass fraction at different measurement locations in the acetone spray. The uncertainty in
$R_{n\ast y}$
) between fluctuations of number density (for different droplet size classes) and vapour mass fraction at different measurement locations in the acetone spray. The uncertainty in
![]() $R_{n\ast y}$
was approximately
$R_{n\ast y}$
was approximately
![]() $\pm 0.05$
with 95 % confidence interval.
$\pm 0.05$
with 95 % confidence interval.
It can be observed in figure 13 that the correlation is always positive, which means that positive/negative fluctuations of droplet number density results in higher/lower vapour mass fraction than the mean value at any instant in time. Also, the correlation is stronger away from the spray axis. This is in agreement with the scatter plots of figure 12, and the discussion thereafter. At any measurement location,
![]() $R_{n\ast y}$
varies inversely with droplet size. Even if the droplet evaporation rate is higher for larger droplets (see (1.4)), since the smaller droplet size class dominates the droplet size distribution, the respective contribution to vapour mass fraction from smaller droplet sizes is higher. For any droplet size class, it can be argued that the relative magnitude of
$R_{n\ast y}$
varies inversely with droplet size. Even if the droplet evaporation rate is higher for larger droplets (see (1.4)), since the smaller droplet size class dominates the droplet size distribution, the respective contribution to vapour mass fraction from smaller droplet sizes is higher. For any droplet size class, it can be argued that the relative magnitude of
![]() $R_{n\ast y}$
at different radial measurement locations suggests the mode of droplet evaporation: while larger values indicate individual droplet evaporation, smaller values of the correlation signify group evaporation.
$R_{n\ast y}$
at different radial measurement locations suggests the mode of droplet evaporation: while larger values indicate individual droplet evaporation, smaller values of the correlation signify group evaporation.

Figure 14. Correlation coefficient of the fluctuations of droplet number density and vapour mass fraction,
![]() $R_{n\ast y}$
, for different window sizes and measurement locations for droplet sizes of (a) 15–30
$R_{n\ast y}$
, for different window sizes and measurement locations for droplet sizes of (a) 15–30
![]() $\unicode[STIX]{x03BC}\text{m}$
, (b) 30–45
$\unicode[STIX]{x03BC}\text{m}$
, (b) 30–45
![]() $\unicode[STIX]{x03BC}\text{m}$
and (c) 45–60
$\unicode[STIX]{x03BC}\text{m}$
and (c) 45–60
![]() $\unicode[STIX]{x03BC}\text{m}$
.
$\unicode[STIX]{x03BC}\text{m}$
.
Due to their partial response to the gas motion, the droplets are associated with the slip velocity (see figure 8) such that the released vapour from droplets may lead or lag the droplet motion. In such a case, it is important to recall the effect of droplet–gas slip on the correlation
![]() $R_{n\ast y}$
, which, however, cannot be discerned from figure 13 since the current dimensions of the measurement area (
$R_{n\ast y}$
, which, however, cannot be discerned from figure 13 since the current dimensions of the measurement area (
![]() $8\times 12~\text{mm}^{2}$
) are of the order of the large-scale eddies of the carrier-phase flow. Hence,
$8\times 12~\text{mm}^{2}$
) are of the order of the large-scale eddies of the carrier-phase flow. Hence,
![]() $R_{n\ast y}$
was also calculated for smaller window sizes, one-half and one-quarter of the measurement window dimensions (i.e.
$R_{n\ast y}$
was also calculated for smaller window sizes, one-half and one-quarter of the measurement window dimensions (i.e.
![]() $4\times 6~\text{mm}^{2}$
and
$4\times 6~\text{mm}^{2}$
and
![]() $2\times 3~\text{mm}^{2}$
, respectively) for droplets of the three size classes. The statistical uncertainty of
$2\times 3~\text{mm}^{2}$
, respectively) for droplets of the three size classes. The statistical uncertainty of
![]() $R_{n\ast y}$
increases for smaller window size, and was found to be
$R_{n\ast y}$
increases for smaller window size, and was found to be
![]() $\pm 0.06$
and
$\pm 0.06$
and
![]() $\pm 0.15$
for the
$\pm 0.15$
for the
![]() $4\times 6~\text{mm}^{2}$
and
$4\times 6~\text{mm}^{2}$
and
![]() $2\times 3~\text{mm}^{2}$
windows respectively. Figure 14 shows the comparison of
$2\times 3~\text{mm}^{2}$
windows respectively. Figure 14 shows the comparison of
![]() $R_{n\ast y}$
for different measurement locations for the three window sizes. It can be observed that for any window size, the correlation is smaller for larger droplet size at all measurement locations, as observed before. Importantly, the magnitude of
$R_{n\ast y}$
for different measurement locations for the three window sizes. It can be observed that for any window size, the correlation is smaller for larger droplet size at all measurement locations, as observed before. Importantly, the magnitude of
![]() $R_{n\ast y}$
decreases for smaller window sizes (by approximately 30 % and 50 % for windows of
$R_{n\ast y}$
decreases for smaller window sizes (by approximately 30 % and 50 % for windows of
![]() $4\times 6~\text{mm}^{2}$
and
$4\times 6~\text{mm}^{2}$
and
![]() $2\times 3~\text{mm}^{2}$
, respectively), implying the role of droplet–gas slip, which results in spatial disparity between the location of droplets and vapour. Due to the larger statistical uncertainty for the smallest window size, the radial increase of
$2\times 3~\text{mm}^{2}$
, respectively), implying the role of droplet–gas slip, which results in spatial disparity between the location of droplets and vapour. Due to the larger statistical uncertainty for the smallest window size, the radial increase of
![]() $R_{n\ast y}$
cannot be observed, unlike for the other window sizes.
$R_{n\ast y}$
cannot be observed, unlike for the other window sizes.
3.3.2 Correlation between droplet velocity and vapour mass fraction
As mentioned earlier, since in our experiments small droplets (15–30
![]() $\unicode[STIX]{x03BC}\text{m}$
) can be assumed to follow fairly well the gas velocity fluctuations, the correlation between the 15–30
$\unicode[STIX]{x03BC}\text{m}$
) can be assumed to follow fairly well the gas velocity fluctuations, the correlation between the 15–30
![]() $\unicode[STIX]{x03BC}\text{m}$
droplet velocity and vapour mass fraction can elucidate the effects of gas turbulence on the droplet evaporation rate. Figure 15 presents the scatter plot between instantaneous fluctuations of droplet velocity and vapour mass fraction for both axial and radial velocity components of 15–30
$\unicode[STIX]{x03BC}\text{m}$
droplet velocity and vapour mass fraction can elucidate the effects of gas turbulence on the droplet evaporation rate. Figure 15 presents the scatter plot between instantaneous fluctuations of droplet velocity and vapour mass fraction for both axial and radial velocity components of 15–30
![]() $\unicode[STIX]{x03BC}\text{m}$
droplets for a measurement location at
$\unicode[STIX]{x03BC}\text{m}$
droplets for a measurement location at
![]() $R=0$
mm. It is interesting to observe that instantaneous fluctuations of droplet velocity are positively correlated to fluctuations of vapour mass fraction. This means increase/decrease of gas velocity fluctuations results in similar variation of the droplet evaporation rate. The correlation is much stronger for axial droplet velocity (figure 15
a) in comparison to the radial component (figure 15
b), which is expected since there is strong anisotropy at the spray centre.
$R=0$
mm. It is interesting to observe that instantaneous fluctuations of droplet velocity are positively correlated to fluctuations of vapour mass fraction. This means increase/decrease of gas velocity fluctuations results in similar variation of the droplet evaporation rate. The correlation is much stronger for axial droplet velocity (figure 15
a) in comparison to the radial component (figure 15
b), which is expected since there is strong anisotropy at the spray centre.

Figure 15. Scatter plot of fluctuations of velocity of 15–30
![]() $\unicode[STIX]{x03BC}\text{m}$
droplets (approximating the gas flow velocity fluctuations) and vapour mass fraction at
$\unicode[STIX]{x03BC}\text{m}$
droplets (approximating the gas flow velocity fluctuations) and vapour mass fraction at
![]() $R=0$
mm for (a) axial velocity and (b) radial velocity.
$R=0$
mm for (a) axial velocity and (b) radial velocity.
Next we calculate the normalized correlations for the considered droplet size classes and different measurement locations. The correlation coefficients, denoted as
![]() $R_{u\ast y}$
and
$R_{u\ast y}$
and
![]() $R_{v\ast y}$
, can be expressed for droplet size class
$R_{v\ast y}$
, can be expressed for droplet size class
![]() $D$
as
$D$
as
where
![]() $u_{r}$
and
$u_{r}$
and
![]() $v_{r}$
are the r.m.s. of axial and radial velocity fluctuations for size class
$v_{r}$
are the r.m.s. of axial and radial velocity fluctuations for size class
![]() $D$
. Figure 16 presents the results. The statistical uncertainty for the correlation coefficients was approximately
$D$
. Figure 16 presents the results. The statistical uncertainty for the correlation coefficients was approximately
![]() $\pm 0.05$
with 95 % confidence interval. Unlike the correlation between droplet number density and vapour mass fraction (
$\pm 0.05$
with 95 % confidence interval. Unlike the correlation between droplet number density and vapour mass fraction (
![]() $R_{n\ast y}$
) as presented earlier (figure 13), both
$R_{n\ast y}$
) as presented earlier (figure 13), both
![]() $R_{u\ast y}$
and
$R_{u\ast y}$
and
![]() $R_{v\ast y}$
are nearly independent of droplet size, since their
$R_{v\ast y}$
are nearly independent of droplet size, since their
![]() $St_{L}$
are not significantly different, although
$St_{L}$
are not significantly different, although
![]() $R_{v\ast y}$
reduces slightly with droplet size.
$R_{v\ast y}$
reduces slightly with droplet size.
![]() $R_{u\ast y}$
is nearly invariant (
$R_{u\ast y}$
is nearly invariant (
![]() ${\approx}0.6$
) across the spray and higher than
${\approx}0.6$
) across the spray and higher than
![]() $R_{v\ast y}$
for all measurement locations.
$R_{v\ast y}$
for all measurement locations.
![]() $R_{v\ast y}$
is nearly zero at the spray centre but increases towards the spray edge as radial transport of droplets becomes more important.
$R_{v\ast y}$
is nearly zero at the spray centre but increases towards the spray edge as radial transport of droplets becomes more important.

Figure 16. Correlation coefficient between fluctuations of droplet velocity and vapour mass fraction for different droplet size classes and measurement locations for (a) axial velocity and (b) radial velocity components.
Although in the past considerable research work has been reported concerning the effect of turbulence on evaporation rate of suspended droplets (for example, see Gökalp et al.
Reference Gökalp, Chauveau, Simon and Chesneau1992; Birouk et al.
Reference Birouk, Chauveau, Sarh, Quilgars and Gökalp1996; Birouk & Toth Reference Birouk and Toth2015), there is no general consensus yet on the role of air turbulence in a spray. According to Gökalp et al. (Reference Gökalp, Chauveau, Simon and Chesneau1992), a way to evaluate the role of turbulence in droplet evaporation is by considering the vaporization Damköhler number (
![]() $Da_{v}$
), which is the ratio of the time scale of turbulent eddies (
$Da_{v}$
), which is the ratio of the time scale of turbulent eddies (
![]() $\unicode[STIX]{x1D70F}_{g}$
) and droplet evaporation time (
$\unicode[STIX]{x1D70F}_{g}$
) and droplet evaporation time (
![]() $\unicode[STIX]{x1D70F}_{v}$
). For two droplets of different volatility but the same size subjected to the same turbulent flow field, smaller
$\unicode[STIX]{x1D70F}_{v}$
). For two droplets of different volatility but the same size subjected to the same turbulent flow field, smaller
![]() $Da_{v}$
implies a stronger influence of turbulence on droplet evaporation. A single droplet evaporation study by the same authors focused on very low values of
$Da_{v}$
implies a stronger influence of turbulence on droplet evaporation. A single droplet evaporation study by the same authors focused on very low values of
![]() $Da_{v}$
(
$Da_{v}$
(
![]() $\ll 1$
) due to their large initial droplet size (approximately 1 mm), which was of the same order as the integral length scale. However, this is not true in technical applications of sprays. For the present case,
$\ll 1$
) due to their large initial droplet size (approximately 1 mm), which was of the same order as the integral length scale. However, this is not true in technical applications of sprays. For the present case,
![]() $Da_{v}$
was calculated considering the characteristic time scale of energy-containing eddies of the gas flow turbulence (see table 1) and the theoretical droplet evaporation time, since in the present experiments the evaporation rate of individual droplets of the spray cannot be measured as this requires Lagrangian tracking of the droplets. The theoretical evaporation time of a droplet (whose initial size
$Da_{v}$
was calculated considering the characteristic time scale of energy-containing eddies of the gas flow turbulence (see table 1) and the theoretical droplet evaporation time, since in the present experiments the evaporation rate of individual droplets of the spray cannot be measured as this requires Lagrangian tracking of the droplets. The theoretical evaporation time of a droplet (whose initial size
![]() $D_{o}$
is equal to the measured SMD in our experiments) was calculated based on the
$D_{o}$
is equal to the measured SMD in our experiments) was calculated based on the
![]() $d^{2}$
-law according to (3.2):
$d^{2}$
-law according to (3.2):
where the evaporation constant
![]() $K_{v}=8(\unicode[STIX]{x1D70C}/\unicode[STIX]{x1D70C}_{l})D_{v}\ln (1+B)Sh$
. This leads to
$K_{v}=8(\unicode[STIX]{x1D70C}/\unicode[STIX]{x1D70C}_{l})D_{v}\ln (1+B)Sh$
. This leads to
![]() $Da_{v}\approx 0.4$
and 1.3 at locations
$Da_{v}\approx 0.4$
and 1.3 at locations
![]() $R=0$
mm and 45 mm, respectively, which means the evaporation time of isolated droplets is comparable to the large eddy time scale of the surrounding turbulent flow. Thus, the gas-phase turbulence can influence the droplet evaporation rate. In order to evaluate the role of turbulence on droplet evaporation one can also compare the Stefan velocity (
$R=0$
mm and 45 mm, respectively, which means the evaporation time of isolated droplets is comparable to the large eddy time scale of the surrounding turbulent flow. Thus, the gas-phase turbulence can influence the droplet evaporation rate. In order to evaluate the role of turbulence on droplet evaporation one can also compare the Stefan velocity (
![]() $v_{s}$
) and turbulent velocity fluctuations of the carrier-phase velocity (
$v_{s}$
) and turbulent velocity fluctuations of the carrier-phase velocity (
![]() $u_{r}$
). For an initial droplet size equal to the measured SMD, the Stefan velocity can be calculated as
$u_{r}$
). For an initial droplet size equal to the measured SMD, the Stefan velocity can be calculated as
The ratio
![]() $v_{s}/u_{r}$
was found to be approximately equal to 0.15 and 0.22 at
$v_{s}/u_{r}$
was found to be approximately equal to 0.15 and 0.22 at
![]() $R=0$
mm and 45 mm respectively, which values are less than the corresponding
$R=0$
mm and 45 mm respectively, which values are less than the corresponding
![]() $Da_{v}$
. However, it conveys the same information, as described above in the context of the
$Da_{v}$
. However, it conveys the same information, as described above in the context of the
![]() $Da_{v}$
, that the evaporation speed of the droplets is comparable to turbulent velocity fluctuations, and turbulence effects on the evaporation of the droplets are higher at the spray centre as
$Da_{v}$
, that the evaporation speed of the droplets is comparable to turbulent velocity fluctuations, and turbulence effects on the evaporation of the droplets are higher at the spray centre as
![]() $v_{s}/u_{r}$
is lower compared to that close to the spray edge. Here, we note that in sprays, unlike in single droplet evaporation studies, turbulence has an indirect effect on droplet evaporation through droplet dispersion leading to interaction between vapour from neighbouring droplets. The influence is more significant when droplets tend to form clusters due to their interaction with the flow turbulence, resulting in reduction of inter-droplet distance and therefore evaporation rate. Thus,
$v_{s}/u_{r}$
is lower compared to that close to the spray edge. Here, we note that in sprays, unlike in single droplet evaporation studies, turbulence has an indirect effect on droplet evaporation through droplet dispersion leading to interaction between vapour from neighbouring droplets. The influence is more significant when droplets tend to form clusters due to their interaction with the flow turbulence, resulting in reduction of inter-droplet distance and therefore evaporation rate. Thus,
![]() $\unicode[STIX]{x1D70F}_{v}$
increases and
$\unicode[STIX]{x1D70F}_{v}$
increases and
![]() $Da_{v}$
is smaller. This explains the strong correlations observed in the above figures.
$Da_{v}$
is smaller. This explains the strong correlations observed in the above figures.
In summary, the droplet–vapour correlations presented above provide useful information regarding the interaction between the two phases in sprays. However, the question remains as to what factors govern the correlation between local vapour mass fraction and droplet properties: Should this be due to local evaporation, mixing or advection from upstream? We attempt to explain this below. In our experiments the residence time of droplets within a measurement window is approximately 5–10 ms, while the droplet evaporation time is typically 40–50 ms, as predicted by the convection corrected
![]() $d^{2}$
-law. The actual droplet evaporation time may be somewhat higher due to droplet clustering resulting in evaporation of the droplet cloud rather than individual droplets. In addition, the time scale of vapour diffusion across the measurement area is much larger (approximately 1 s). Hence, the correlation between instantaneous droplet number density and the local evaporation of droplets and/or mixing must be very weak. On the other hand, since the density difference between vapour and air is not significant and the droplet Stokes number (based on the large eddy scale) is small, the vapour around droplets is carried along with the carrier air flow. Hence, the instantaneous correlation between the droplet number density and velocity with surrounding local vapour concentration is attributed to advection of vapour.
$d^{2}$
-law. The actual droplet evaporation time may be somewhat higher due to droplet clustering resulting in evaporation of the droplet cloud rather than individual droplets. In addition, the time scale of vapour diffusion across the measurement area is much larger (approximately 1 s). Hence, the correlation between instantaneous droplet number density and the local evaporation of droplets and/or mixing must be very weak. On the other hand, since the density difference between vapour and air is not significant and the droplet Stokes number (based on the large eddy scale) is small, the vapour around droplets is carried along with the carrier air flow. Hence, the instantaneous correlation between the droplet number density and velocity with surrounding local vapour concentration is attributed to advection of vapour.
3.3.3 Correlation between droplet number density of different size classes
The correlation coefficient between fluctuations of droplet number density of different droplet size classes, denoted as
![]() $R_{n_{i}\ast n_{j}}$
, is useful for understanding droplet dispersion and clustering in isothermal sprays (Sahu et al.
Reference Sahu, Hardalupas and Taylor2016) and can provide an insight into the dispersion of evaporating droplets. The correlation coefficient of the fluctuations of droplet number density of two droplet size classes
$R_{n_{i}\ast n_{j}}$
, is useful for understanding droplet dispersion and clustering in isothermal sprays (Sahu et al.
Reference Sahu, Hardalupas and Taylor2016) and can provide an insight into the dispersion of evaporating droplets. The correlation coefficient of the fluctuations of droplet number density of two droplet size classes
![]() $D_{i}$
and
$D_{i}$
and
![]() $D_{j}$
can be expressed as
$D_{j}$
can be expressed as
Large values of
![]() $R_{n_{i}\ast n_{j}}$
imply that any increase or decrease in droplet concentration of one size class is accompanied by a similar variation for the other, which means that droplets belonging to both size classes respond similarly to the gas motion and therefore may both contribute to droplet clustering affecting droplet evaporation. In the present case,
$R_{n_{i}\ast n_{j}}$
imply that any increase or decrease in droplet concentration of one size class is accompanied by a similar variation for the other, which means that droplets belonging to both size classes respond similarly to the gas motion and therefore may both contribute to droplet clustering affecting droplet evaporation. In the present case,
![]() $R_{n_{i}\ast n_{j}}$
is obtained for both acetone and water sprays, and the results are plotted in figure 17 for different measurement locations,
$R_{n_{i}\ast n_{j}}$
is obtained for both acetone and water sprays, and the results are plotted in figure 17 for different measurement locations,
![]() $R$
. The statistical uncertainty in the correlation was approximately
$R$
. The statistical uncertainty in the correlation was approximately
![]() $\pm 0.05$
–0.07 with 95 % confidence interval.
$\pm 0.05$
–0.07 with 95 % confidence interval.

Figure 17. Correlation coefficient (
![]() $R_{n_{i}\ast n_{j}}$
) between fluctuations of number density of different droplet size classes as a function of distance from spray axis. The uncertainty in the correlation was approximately
$R_{n_{i}\ast n_{j}}$
) between fluctuations of number density of different droplet size classes as a function of distance from spray axis. The uncertainty in the correlation was approximately
![]() $\pm 0.05$
–0.07 with 95 % confidence interval. The open and closed symbols refer to water and acetone droplets, respectively.
$\pm 0.05$
–0.07 with 95 % confidence interval. The open and closed symbols refer to water and acetone droplets, respectively.
Figure 17 shows
![]() $R_{n_{i}\ast n_{j}}$
for the three combinations of droplet size classes considered in the present case (i.e.
$R_{n_{i}\ast n_{j}}$
for the three combinations of droplet size classes considered in the present case (i.e.
![]() $R_{n_{1}\ast n_{2}}$
,
$R_{n_{1}\ast n_{2}}$
,
![]() $R_{n_{2}\ast n_{3}}$
and
$R_{n_{2}\ast n_{3}}$
and
![]() $R_{n_{1}\ast n_{3}}$
, where 1, 2 and 3 denote increasing order of droplet size classes), which are positive for all cases. It can be observed that for all measurement locations,
$R_{n_{1}\ast n_{3}}$
, where 1, 2 and 3 denote increasing order of droplet size classes), which are positive for all cases. It can be observed that for all measurement locations,
![]() $R_{n_{1}\ast n_{2}}>R_{n_{2}\ast n_{3}}>R_{n_{1}\ast n_{3}}$
, which is due to increasingly poor response of the large droplet size class to gas motion. For water droplets
$R_{n_{1}\ast n_{2}}>R_{n_{2}\ast n_{3}}>R_{n_{1}\ast n_{3}}$
, which is due to increasingly poor response of the large droplet size class to gas motion. For water droplets
![]() $R_{n_{i}\ast n_{j}}$
increases considerably towards the spray edge due to the better response of the droplets (smaller
$R_{n_{i}\ast n_{j}}$
increases considerably towards the spray edge due to the better response of the droplets (smaller
![]() $St_{L}$
). However, for acetone droplets, the correlation coefficients for any combination of droplet size classes are almost spatially uniform across the spray, and higher in comparison to water droplets, especially close to the spray centre. This is attributed to evaporation of acetone droplets, which caused increased fluctuations of droplet number density compared to the water spray (figure 5
b). Thus,
$St_{L}$
). However, for acetone droplets, the correlation coefficients for any combination of droplet size classes are almost spatially uniform across the spray, and higher in comparison to water droplets, especially close to the spray centre. This is attributed to evaporation of acetone droplets, which caused increased fluctuations of droplet number density compared to the water spray (figure 5
b). Thus,
![]() $R_{n_{i}\ast n_{j}}$
can be considered as an indication of existence of droplet clustering, which is more prominent in the acetone spray than the water spray.
$R_{n_{i}\ast n_{j}}$
can be considered as an indication of existence of droplet clustering, which is more prominent in the acetone spray than the water spray.
3.3.4 Group evaporation number (
 $G$
)
$G$
)
As mentioned earlier, Chiu & coworkers (Chiu & Liu Reference Chiu and Liu1977; Chiu et al.
Reference Chiu, Kim and Croke1982; Chiu & Kim Reference Chiu and Kim1983) characterized group burning of droplets by the group combustion number,
![]() $G$
. For a mono-dispersed spherical cloud of droplets, the magnitude of
$G$
. For a mono-dispersed spherical cloud of droplets, the magnitude of
![]() $G$
specifically depends on droplet diameter (
$G$
specifically depends on droplet diameter (
![]() $\overline{D}$
), number of droplets (
$\overline{D}$
), number of droplets (
![]() $n_{T}$
) and inter-droplet distance (
$n_{T}$
) and inter-droplet distance (
![]() $l_{d}$
), and can be expressed as
$l_{d}$
), and can be expressed as
where
![]() $Re$
is the droplet Reynolds number,
$Re$
is the droplet Reynolds number,
![]() $Sc$
and
$Sc$
and
![]() $Le$
are the gas Schmidt and the Lewis numbers respectively and
$Le$
are the gas Schmidt and the Lewis numbers respectively and
![]() $S$
is the non-dimensional separation distance such that
$S$
is the non-dimensional separation distance such that
![]() $S=(l_{d}/10D)/(1+0.276Re^{0.5}Sc^{0.33})$
. With a progressive increase in the magnitude of
$S=(l_{d}/10D)/(1+0.276Re^{0.5}Sc^{0.33})$
. With a progressive increase in the magnitude of
![]() $G$
, different modes of group combustion may prevail (Sirignano Reference Sirignano1999), for example, single droplet combustion (
$G$
, different modes of group combustion may prevail (Sirignano Reference Sirignano1999), for example, single droplet combustion (
![]() $G\ll 1$
), internal group combustion (
$G\ll 1$
), internal group combustion (
![]() $G<1$
), external group combustion (
$G<1$
), external group combustion (
![]() $G>1$
) and external sheath combustion (
$G>1$
) and external sheath combustion (
![]() $G\gg 1$
).
$G\gg 1$
).
For a reacting spray, a flame surrounding a cloud of droplets results in the group burning mode of the droplet cloud. In the present work we identify droplet clustering as one of the reasons behind droplet cloud formation, though in the context of an evaporating, non-reacting spray. Away from the injector exit, dynamic interaction of droplets with the surrounding turbulent air flow leads to formation of clusters of droplets. The droplet clusters are dynamic entities and the droplets within a cluster remain close to each other for a time scale comparable to the characteristic turbulence time scale of the surrounding air flow (Monchaux et al.
Reference Monchaux, Bourgoin and Cartellier2012). Although the convection of the vapour away from the droplet vicinity is the controlling factor for droplet evaporation, however, in our case, since the droplet Reynolds number is small (
![]() $Re\approx 0.1$
), the diffusion plays an important role in addition to turbulence. The diffusion of vapour from the droplet surface is controlled by the gradient of the vapour concentration. Due to smaller separation distance between droplets within a cluster, the gradient in vapour concentration at the droplet surface is smaller than that for an isolated droplet. Hence, the overall evaporation rate of a droplet cluster is expected to be smaller than that for an isolated droplet. Earlier, several works and review articles (for instance, Reveillon & Vervisch Reference Reveillon and Vervisch2000; Kronenburg Reference Kronenburg2007; Reveillon & Demoulin Reference Reveillon and Demoulin2007; Jenny, Roekaerts & Beishuizen Reference Jenny, Roekaerts and Beishuizen2012) identified that the droplet segregation strongly affects the evolution of the vapour mixture fraction and insisted on lack of models to account for such effects. However, experimental work highlighting the above effect is rare. The measurement of the local group evaporation number is a way to quantify the change of evaporation rate due to the above effects. For non-reacting and evaporating sprays
$Re\approx 0.1$
), the diffusion plays an important role in addition to turbulence. The diffusion of vapour from the droplet surface is controlled by the gradient of the vapour concentration. Due to smaller separation distance between droplets within a cluster, the gradient in vapour concentration at the droplet surface is smaller than that for an isolated droplet. Hence, the overall evaporation rate of a droplet cluster is expected to be smaller than that for an isolated droplet. Earlier, several works and review articles (for instance, Reveillon & Vervisch Reference Reveillon and Vervisch2000; Kronenburg Reference Kronenburg2007; Reveillon & Demoulin Reference Reveillon and Demoulin2007; Jenny, Roekaerts & Beishuizen Reference Jenny, Roekaerts and Beishuizen2012) identified that the droplet segregation strongly affects the evolution of the vapour mixture fraction and insisted on lack of models to account for such effects. However, experimental work highlighting the above effect is rare. The measurement of the local group evaporation number is a way to quantify the change of evaporation rate due to the above effects. For non-reacting and evaporating sprays
![]() $G$
can be termed the group evaporation number, which indicates the significance of the gross droplet evaporation rate relative to the inward diffusion rate of air. Since for our flow conditions the droplet Reynolds number is small, and for mixture of acetone vapour and air
$G$
can be termed the group evaporation number, which indicates the significance of the gross droplet evaporation rate relative to the inward diffusion rate of air. Since for our flow conditions the droplet Reynolds number is small, and for mixture of acetone vapour and air
![]() $Sc\approx 1$
and
$Sc\approx 1$
and
![]() $Le\approx 1$
, equation (3.12) becomes
$Le\approx 1$
, equation (3.12) becomes
Since the expression for
![]() $G$
(3.12) was derived for droplets uniformly spaced within a cloud of droplets, the volume occupied by the cloud approximately equals to
$G$
(3.12) was derived for droplets uniformly spaced within a cloud of droplets, the volume occupied by the cloud approximately equals to
![]() $n_{T}\times \unicode[STIX]{x03C0}{l_{d}}^{3}/6$
. Thus, for a spherical droplet cloud of size
$n_{T}\times \unicode[STIX]{x03C0}{l_{d}}^{3}/6$
. Thus, for a spherical droplet cloud of size
![]() $L_{c}$
,
$L_{c}$
,
Thus, equation (3.14) can be expressed as
The group evaporation number is evaluated using (3.16) instead of (3.14); the reason behind this will be explained later. However, in such a case, two challenges are encountered: (i) an estimation of the size of droplet clouds or clusters is essential, and (ii) the droplet cluster passing through the measurement region must be identified, since (3.16) is applicable to droplet clouds only. Both of these aspects are discussed below.
3.3.5 Radial distribution function (RDF)
In the present case, the droplet cluster dimension (
![]() $L_{c}$
), required for (3.16), was obtained by evaluating the radial distribution function (RDF) of the droplets for different measurement locations in the spray. RDF essentially measures the probability of finding a second droplet at a given separation distance from a reference droplet, compared to a case where the droplets are homogeneously distributed (Sundaram & Collins Reference Sundaram and Collins1999; Salazar et al.
Reference Salazar, de Jong, Cao, Woodward, Meng and Collins2008). It is computed from a field of
$L_{c}$
), required for (3.16), was obtained by evaluating the radial distribution function (RDF) of the droplets for different measurement locations in the spray. RDF essentially measures the probability of finding a second droplet at a given separation distance from a reference droplet, compared to a case where the droplets are homogeneously distributed (Sundaram & Collins Reference Sundaram and Collins1999; Salazar et al.
Reference Salazar, de Jong, Cao, Woodward, Meng and Collins2008). It is computed from a field of
![]() $M$
number of droplets by binning the droplet pairs according to their separation distance (
$M$
number of droplets by binning the droplet pairs according to their separation distance (
![]() $r$
), and calculating the function
$r$
), and calculating the function
where
![]() $P_{i}$
is the number of droplet pairs separated by a distance
$P_{i}$
is the number of droplet pairs separated by a distance
![]() $r_{i}\pm \unicode[STIX]{x1D6FF}r/2$
, the parameter
$r_{i}\pm \unicode[STIX]{x1D6FF}r/2$
, the parameter
![]() $r_{i}$
refers to the discrete values of separation distance, where the RDF is calculated,
$r_{i}$
refers to the discrete values of separation distance, where the RDF is calculated,
![]() $\unicode[STIX]{x1D6FF}A_{i}$
is the area of the discrete shell located at
$\unicode[STIX]{x1D6FF}A_{i}$
is the area of the discrete shell located at
![]() $r_{i}$
,
$r_{i}$
,
![]() $P=M(M-1)/2$
is the total number of pairs and
$P=M(M-1)/2$
is the total number of pairs and
![]() $A$
is the total area of the measurement region. Effectively, the values of
$A$
is the total area of the measurement region. Effectively, the values of
![]() $\text{RDF}>1$
refer to the degree of preferential accumulation or clustering of droplets due to their interaction with turbulent eddies, while values of
$\text{RDF}>1$
refer to the degree of preferential accumulation or clustering of droplets due to their interaction with turbulent eddies, while values of
![]() $\text{RDF}<1$
represent voids. Thus, the value of radial separation (
$\text{RDF}<1$
represent voids. Thus, the value of radial separation (
![]() $r$
) for which
$r$
) for which
![]() $\text{RDF}(r)\approx 1$
provides an estimate of the length scale of the clusters (
$\text{RDF}(r)\approx 1$
provides an estimate of the length scale of the clusters (
![]() $L_{c}$
). In the present work, measurement of RDF was achieved by ILIDS measurements of droplets. We have verified in our previous work (Sahu et al.
Reference Sahu, Hardalupas and Taylor2016) that calculation of
$L_{c}$
). In the present work, measurement of RDF was achieved by ILIDS measurements of droplets. We have verified in our previous work (Sahu et al.
Reference Sahu, Hardalupas and Taylor2016) that calculation of
![]() $L_{c}$
by an RDF based on ILIDS agrees well with the ‘droplet counting in a cell’ approach (Fessler et al.
Reference Fessler, Kulick and Eaton1994) based on focused spray droplet images. The expression for
$L_{c}$
by an RDF based on ILIDS agrees well with the ‘droplet counting in a cell’ approach (Fessler et al.
Reference Fessler, Kulick and Eaton1994) based on focused spray droplet images. The expression for
![]() $G$
in (3.16) is derived for uniform size of droplets in a cloud. However, a droplet cluster may contain droplets of different sizes. Thus,
$G$
in (3.16) is derived for uniform size of droplets in a cloud. However, a droplet cluster may contain droplets of different sizes. Thus,
![]() $L_{c}$
should be determined for an average droplet size. However, before presenting this we will explain the tendency of droplets of different sizes to form clusters, and in such a case whether the corresponding length scales of droplet clusters are different.
$L_{c}$
should be determined for an average droplet size. However, before presenting this we will explain the tendency of droplets of different sizes to form clusters, and in such a case whether the corresponding length scales of droplet clusters are different.

Figure 18. Evaluation of RDF for the radial measurement locations in the acetone spray at (a)
![]() $R=0$
mm (
$R=0$
mm (
![]() $L=12$
mm) and (b)
$L=12$
mm) and (b)
![]() $R=45$
mm (
$R=45$
mm (
![]() $L=17$
mm) conditional on droplet size.
$L=17$
mm) conditional on droplet size.
Figure 18 presents RDFs for radial measurement locations in the acetone spray at
![]() $R=0$
mm and 45 mm respectively. The RDFs are calculated conditional on droplet size classes, which means that only droplets of that size class are assumed to be present in an ILIDS image. The RDFs are plotted for different
$R=0$
mm and 45 mm respectively. The RDFs are calculated conditional on droplet size classes, which means that only droplets of that size class are assumed to be present in an ILIDS image. The RDFs are plotted for different
![]() $r$
values normalized with the local integral length scale,
$r$
values normalized with the local integral length scale,
![]() $L$
, which is larger towards the spray edge (table 1). The error bars indicate uncertainty in the RDF with 95 % confidence interval. The increments in
$L$
, which is larger towards the spray edge (table 1). The error bars indicate uncertainty in the RDF with 95 % confidence interval. The increments in
![]() $r_{i}$
, and
$r_{i}$
, and
![]() $\unicode[STIX]{x1D6FF}r_{i}/2$
were chosen to be 1 mm and 2 mm respectively, as a compromise between losing the spatial resolution and having enough droplets to obtain appropriate statistics. Similar trends were found for RDFs at other measurement locations, and are not presented here. It can be observed that the RDF values are higher for larger droplet sizes due to the smaller droplet number count per unit area in an image (low
$\unicode[STIX]{x1D6FF}r_{i}/2$
were chosen to be 1 mm and 2 mm respectively, as a compromise between losing the spatial resolution and having enough droplets to obtain appropriate statistics. Similar trends were found for RDFs at other measurement locations, and are not presented here. It can be observed that the RDF values are higher for larger droplet sizes due to the smaller droplet number count per unit area in an image (low
![]() $P/A$
). This trend is in agreement with fluctuations of droplet number density (relative to the mean) as shown in figure 5(b). The length scale of the droplet clusters is approximately 0.1
$P/A$
). This trend is in agreement with fluctuations of droplet number density (relative to the mean) as shown in figure 5(b). The length scale of the droplet clusters is approximately 0.1
![]() $L$
–0.3
$L$
–0.3
![]() $L$
, as shown in figure 18, which means the energy-containing eddies influence dispersion of droplets similarly to particle-laden jet flows (Longmire & Eaton Reference Longmire and Eaton1992). Also, the cluster dimension is larger for higher droplet size classes. Thus, the larger droplets have a greater tendency to preferentially accumulate in some regions of the flow. It is also observed in figure 18 that the RDF values increase for the location of
$L$
, as shown in figure 18, which means the energy-containing eddies influence dispersion of droplets similarly to particle-laden jet flows (Longmire & Eaton Reference Longmire and Eaton1992). Also, the cluster dimension is larger for higher droplet size classes. Thus, the larger droplets have a greater tendency to preferentially accumulate in some regions of the flow. It is also observed in figure 18 that the RDF values increase for the location of
![]() $R=45~$
mm for all droplet size classes in comparison to those for the spray centre. This is justified due to the better response of the droplets towards the edge of the spray as the flow is slower and
$R=45~$
mm for all droplet size classes in comparison to those for the spray centre. This is justified due to the better response of the droplets towards the edge of the spray as the flow is slower and
![]() $St_{L}$
is smaller.
$St_{L}$
is smaller.

Figure 19. Evolution of radial distribution function (RDF) of the spray droplets for increasing radius of separation for the acetone and water sprays at measurement locations
![]() $R=0$
mm and 45 mm.
$R=0$
mm and 45 mm.
In order to estimate the droplet size-averaged
![]() $L_{c}$
, RDF is calculated by considering droplets of all sizes in the ILIDS images. Figure 19 presents such RDFs for the acetone spray at the measurement locations
$L_{c}$
, RDF is calculated by considering droplets of all sizes in the ILIDS images. Figure 19 presents such RDFs for the acetone spray at the measurement locations
![]() $R=0$
mm and 45 mm. The functions are plotted for different radii of separation. The RDF values are close to those of the 15–30
$R=0$
mm and 45 mm. The functions are plotted for different radii of separation. The RDF values are close to those of the 15–30
![]() $\unicode[STIX]{x03BC}\text{m}$
droplets in figure 18, as expected, due to domination of smaller droplets in the droplet population. Figure 19 also shows the RDFs for the water spray for the respective measurement locations in order to assess the effect of droplet evaporation on droplet clustering. For both sprays, the function shifts upward for the
$\unicode[STIX]{x03BC}\text{m}$
droplets in figure 18, as expected, due to domination of smaller droplets in the droplet population. Figure 19 also shows the RDFs for the water spray for the respective measurement locations in order to assess the effect of droplet evaporation on droplet clustering. For both sprays, the function shifts upward for the
![]() $R=45$
mm location implying increase in RDF values and droplet cluster length scale towards the spray boundary. Also, it can be observed that the RDF values are higher (though not significantly) for the acetone spray for all radii of separation – hence the tendency of droplets to form clusters and the cluster dimension increase due to evaporation. As the droplets tend to form clusters, the temporal variation of droplet number density is expected to increase at any spatial location. This is in agreement with the increase in number density fluctuations in figure 5(b), and number density correlation (
$R=45$
mm location implying increase in RDF values and droplet cluster length scale towards the spray boundary. Also, it can be observed that the RDF values are higher (though not significantly) for the acetone spray for all radii of separation – hence the tendency of droplets to form clusters and the cluster dimension increase due to evaporation. As the droplets tend to form clusters, the temporal variation of droplet number density is expected to increase at any spatial location. This is in agreement with the increase in number density fluctuations in figure 5(b), and number density correlation (
![]() $R_{n\ast n}$
) in figure 17.
$R_{n\ast n}$
) in figure 17.
The length scale of the droplet clusters,
![]() $L_{c}$
, in the acetone spray was estimated to be approximately 2–3 mm, which is approximately one-third of the measurement window dimension as depicted in the PLIF images shown in figure 20. As mentioned earlier, since
$L_{c}$
, in the acetone spray was estimated to be approximately 2–3 mm, which is approximately one-third of the measurement window dimension as depicted in the PLIF images shown in figure 20. As mentioned earlier, since
![]() $L_{c}$
is of the order of
$L_{c}$
is of the order of
![]() $L$
, the large scales of the turbulent flow are expected to influence the cluster size. In addition, the large eddies are responsible for the transport of these clusters, and thus the frequency of passage of droplet clusters and inter-cluster spacing at any location in the spray are expected to be governed by the large-scale eddies of the flow (Fessler et al.
Reference Fessler, Kulick and Eaton1994; Sahu et al.
Reference Sahu, Hardalupas and Taylor2016).
$L$
, the large scales of the turbulent flow are expected to influence the cluster size. In addition, the large eddies are responsible for the transport of these clusters, and thus the frequency of passage of droplet clusters and inter-cluster spacing at any location in the spray are expected to be governed by the large-scale eddies of the flow (Fessler et al.
Reference Fessler, Kulick and Eaton1994; Sahu et al.
Reference Sahu, Hardalupas and Taylor2016).
3.3.6 Measurement of group evaporation number
For the present experiments, the droplet residence time at the measurement region (
![]() ${\approx}5$
–10 ms) is smaller than the energy-containing eddy time scale (
${\approx}5$
–10 ms) is smaller than the energy-containing eddy time scale (
![]() ${\approx}21$
–51 ms), which is of the order of the time scale of transport of droplet clusters. Thus, at any time instant about one droplet cluster is expected to be present within the measurement area at any measurement location (the image dimensions are similar to the large eddy length scales of the flow). This is also supported by the visual inspection of the PLIF images at
${\approx}21$
–51 ms), which is of the order of the time scale of transport of droplet clusters. Thus, at any time instant about one droplet cluster is expected to be present within the measurement area at any measurement location (the image dimensions are similar to the large eddy length scales of the flow). This is also supported by the visual inspection of the PLIF images at
![]() $R=0$
mm in figure 20. The group evaporation number (
$R=0$
mm in figure 20. The group evaporation number (
![]() $G$
) is evaluated for different time instants corresponding to passage of a droplet cluster through the measurement window at any radial measurement location in the spray. For instantaneous ILIDS images where droplet clusters are identified,
$G$
) is evaluated for different time instants corresponding to passage of a droplet cluster through the measurement window at any radial measurement location in the spray. For instantaneous ILIDS images where droplet clusters are identified,
![]() $G$
is calculated under the assumption that the characteristic droplet size and inter-droplet distance within a cluster is the spatially averaged droplet size and average droplet separation distance calculated based on all droplets appearing in an instantaneous image.
$G$
is calculated under the assumption that the characteristic droplet size and inter-droplet distance within a cluster is the spatially averaged droplet size and average droplet separation distance calculated based on all droplets appearing in an instantaneous image.

Figure 20. Instantaneous PLIF images of the spray depicting (a) droplet clusters and (b) no clustering at the measurement location
![]() $R=0$
mm. The images are presented in greyscale (0–256) for better visualization.
$R=0$
mm. The images are presented in greyscale (0–256) for better visualization.
Thus, in (3.16), the parameter
![]() $\overline{D}$
is considered as the arithmetic mean diameter (AMD) of droplets identified in an instantaneous ILIDS image such that
$\overline{D}$
is considered as the arithmetic mean diameter (AMD) of droplets identified in an instantaneous ILIDS image such that
 $$\begin{eqnarray}\text{AMD}=\frac{\displaystyle \mathop{\sum }_{i=1}^{n_{Tv}}D_{i}}{n_{Tv}},\end{eqnarray}$$
$$\begin{eqnarray}\text{AMD}=\frac{\displaystyle \mathop{\sum }_{i=1}^{n_{Tv}}D_{i}}{n_{Tv}},\end{eqnarray}$$
where
![]() $D_{i}$
is the size of
$D_{i}$
is the size of
![]() $i$
th droplet and
$i$
th droplet and
![]() $n_{Tv}$
is the total number of droplets identified in the ILIDS image.
$n_{Tv}$
is the total number of droplets identified in the ILIDS image.
The parameter
![]() $l_{d}$
is the average minimum droplet separation distance defined as
$l_{d}$
is the average minimum droplet separation distance defined as
 $$\begin{eqnarray}l_{d}=\frac{\displaystyle \mathop{\sum }_{i=1}^{n_{Tv}}l_{di}}{n_{Tv}},\end{eqnarray}$$
$$\begin{eqnarray}l_{d}=\frac{\displaystyle \mathop{\sum }_{i=1}^{n_{Tv}}l_{di}}{n_{Tv}},\end{eqnarray}$$
where
![]() $l_{di}$
is the minimum separation distance of the
$l_{di}$
is the minimum separation distance of the
![]() $i$
th droplet with respect to any other droplet in the ILIDS image. Since the validation rate of ILIDS image processing (i.e. the ratio of number of droplets identified in the image (
$i$
th droplet with respect to any other droplet in the ILIDS image. Since the validation rate of ILIDS image processing (i.e. the ratio of number of droplets identified in the image (
![]() $n_{Tv}$
) to the total number of droplets actually present within the measurement volume) is approximately 30–50 %,
$n_{Tv}$
) to the total number of droplets actually present within the measurement volume) is approximately 30–50 %,
![]() $n_{Tv}<n_{T}$
, and hence (3.14) cannot be used directly; however, equation (3.16) can be reliably used, since
$n_{Tv}<n_{T}$
, and hence (3.14) cannot be used directly; however, equation (3.16) can be reliably used, since
![]() $l_{d}$
can be uniquely measured by ILIDS.
$l_{d}$
can be uniquely measured by ILIDS.
In order to identify the time instant when droplet clusters pass though the measurement region, the maximum inter-droplet distance (
![]() $l_{d_{max}}$
) is estimated using (3.15) for a given cluster size of
$l_{d_{max}}$
) is estimated using (3.15) for a given cluster size of
![]() $L_{c}$
at any measurement location and for the identified number of droplets,
$L_{c}$
at any measurement location and for the identified number of droplets,
![]() $n_{Tv}$
. The presence of droplet clusters ensures
$n_{Tv}$
. The presence of droplet clusters ensures
![]() $l_{d_{max}}$
is larger than
$l_{d_{max}}$
is larger than
![]() $l_{d}$
(measured directly from the ILIDS image), and so
$l_{d}$
(measured directly from the ILIDS image), and so
![]() $G$
is evaluated using (3.16). If for an instantaneous ILIDS image
$G$
is evaluated using (3.16). If for an instantaneous ILIDS image
![]() $l_{d_{max}}<l_{d}$
, then no clusters are present, and
$l_{d_{max}}<l_{d}$
, then no clusters are present, and
![]() $G$
is not evaluated. The result of the above method is visually depicted in figure 20, as an example which shows some sample PLIF images where droplet clusters could be identified (top images) and when no clusters are observed (bottom images). The boundaries are drawn around groups of droplets to emphasize clustering. Figure 21 shows histograms of ratio of inter-droplet distance to average droplet size (i.e.
$G$
is not evaluated. The result of the above method is visually depicted in figure 20, as an example which shows some sample PLIF images where droplet clusters could be identified (top images) and when no clusters are observed (bottom images). The boundaries are drawn around groups of droplets to emphasize clustering. Figure 21 shows histograms of ratio of inter-droplet distance to average droplet size (i.e.
![]() $l_{d}/\text{AMD}$
) measured for the instantaneous images corresponding to passage of droplet clusters at a measurement location. The results are presented at the locations
$l_{d}/\text{AMD}$
) measured for the instantaneous images corresponding to passage of droplet clusters at a measurement location. The results are presented at the locations
![]() $R=0$
mm and 45 mm. Although the ratio of mean droplet separation to mean droplet size is approximately 20–30, locally the inter-droplet distance can be smaller (
$R=0$
mm and 45 mm. Although the ratio of mean droplet separation to mean droplet size is approximately 20–30, locally the inter-droplet distance can be smaller (
![]() ${<}5$
times the AMD) as the droplets preferentially accumulate in some region of the flow, as a consequence of the interaction between surrounding turbulent air flow. While the studies on mono-sized droplet streams (for instance, Depredurand & Castanet Reference Depredurand, Castanet and Lemoine2010) reported that beyond a separation distance of approximately eight droplet diameters the evaporation of adjacent droplets does not influence each other, in such a case any droplet is accompanied by only two neighbouring droplets; this limit is much larger when a droplet is embedded within a cluster of droplets and collective evaporation of all droplets prevails (for instance, see the experiments for an array of droplets in Imaoka & Sirignano Reference Imaoka and Sirignano2005). An order of magnitude variation in inter-separation distances between droplets can be observed in figure 21, especially at the spray edge. This implies similar variation in the value of
${<}5$
times the AMD) as the droplets preferentially accumulate in some region of the flow, as a consequence of the interaction between surrounding turbulent air flow. While the studies on mono-sized droplet streams (for instance, Depredurand & Castanet Reference Depredurand, Castanet and Lemoine2010) reported that beyond a separation distance of approximately eight droplet diameters the evaporation of adjacent droplets does not influence each other, in such a case any droplet is accompanied by only two neighbouring droplets; this limit is much larger when a droplet is embedded within a cluster of droplets and collective evaporation of all droplets prevails (for instance, see the experiments for an array of droplets in Imaoka & Sirignano Reference Imaoka and Sirignano2005). An order of magnitude variation in inter-separation distances between droplets can be observed in figure 21, especially at the spray edge. This implies similar variation in the value of
![]() $G$
and hence the mode of group evaporation.
$G$
and hence the mode of group evaporation.

Figure 21. Probability of the ratio of mean droplet separation (
![]() $l_{d}$
) to arithmetic mean diameter of droplets identified from instantaneous images of droplet clusters present in the measurement window at locations (a)
$l_{d}$
) to arithmetic mean diameter of droplets identified from instantaneous images of droplet clusters present in the measurement window at locations (a)
![]() $R=0$
mm and (b)
$R=0$
mm and (b)
![]() $R=45$
mm.
$R=45$
mm.

Figure 22. (a) Evolution of mean group evaporation number
![]() $G$
and the standard deviation of its fluctuations (as error bars) at different measurement locations. (b) Distribution of group evaporation number of droplet clusters on an
$G$
and the standard deviation of its fluctuations (as error bars) at different measurement locations. (b) Distribution of group evaporation number of droplet clusters on an
![]() $n_{T}$
–
$n_{T}$
–
![]() $S$
plot for measurement locations
$S$
plot for measurement locations
![]() $R=0$
mm and 45 mm. Iso-
$R=0$
mm and 45 mm. Iso-
![]() $G$
lines derived from (3.13) are shown and indicate different group evaporation regimes.
$G$
lines derived from (3.13) are shown and indicate different group evaporation regimes.
Figure 22(a) presents the evolution of mean group evaporation number
![]() $G$
at different radial measurement locations in the evaporative spray following (3.16), while the r.m.s. of fluctuations of
$G$
at different radial measurement locations in the evaporative spray following (3.16), while the r.m.s. of fluctuations of
![]() $G$
are indicated by error bars. The statistical uncertainty in the calculation of
$G$
are indicated by error bars. The statistical uncertainty in the calculation of
![]() $G$
was approximately
$G$
was approximately
![]() $\pm 5\,\%$
with 95 % confidence interval. The magnitude of the mean
$\pm 5\,\%$
with 95 % confidence interval. The magnitude of the mean
![]() $G$
is between 0.5 and 1, implying the mode of droplet cloud evaporation falls in the regime of internal group evaporation. This regime is characterized by an external ring of individually evaporating droplets centred around a central core of droplets, which evaporate collectively as a group.
$G$
is between 0.5 and 1, implying the mode of droplet cloud evaporation falls in the regime of internal group evaporation. This regime is characterized by an external ring of individually evaporating droplets centred around a central core of droplets, which evaporate collectively as a group.
![]() $G$
decreases from the central spray region towards the spray edge, where the droplets tend to evaporate individually (due to larger droplet spacing) without interacting with each other. Figure 22(b) shows the plot of
$G$
decreases from the central spray region towards the spray edge, where the droplets tend to evaporate individually (due to larger droplet spacing) without interacting with each other. Figure 22(b) shows the plot of
![]() $n_{T}$
versus the non-dimensional separation distance
$n_{T}$
versus the non-dimensional separation distance
![]() $S$
(see (3.13)) at the measurement locations
$S$
(see (3.13)) at the measurement locations
![]() $R=0$
mm and 45 mm. The number of droplets present in a droplet cloud (
$R=0$
mm and 45 mm. The number of droplets present in a droplet cloud (
![]() $n_{T}$
) is estimated from (3.15) by considering the inter-droplet separation at that time instant. Figure 22(b) also indicates constant
$n_{T}$
) is estimated from (3.15) by considering the inter-droplet separation at that time instant. Figure 22(b) also indicates constant
![]() $G$
lines, which indicate various regimes of group evaporation. For
$G$
lines, which indicate various regimes of group evaporation. For
![]() $R=45$
mm, a horizontal shift of the instantaneous values of
$R=45$
mm, a horizontal shift of the instantaneous values of
![]() $G$
towards the line of
$G$
towards the line of
![]() $G=0.01$
can be seen. Significant variations in the magnitude of
$G=0.01$
can be seen. Significant variations in the magnitude of
![]() $G$
can be observed for both measurement locations, which is also evident from the error bars in figure 22(a). The above result signifies the consequence of droplet dispersion on droplet evaporation, indicating not only the fact that even far away from the injector exit collective evaporation of droplets is promoted, but also the mode of group evaporation considerably varies even close to the spray centre. Also, the trend in
$G$
can be observed for both measurement locations, which is also evident from the error bars in figure 22(a). The above result signifies the consequence of droplet dispersion on droplet evaporation, indicating not only the fact that even far away from the injector exit collective evaporation of droplets is promoted, but also the mode of group evaporation considerably varies even close to the spray centre. Also, the trend in
![]() $G$
is opposite to that of
$G$
is opposite to that of
![]() $R_{n\ast y}$
(figure 13) for any droplet size class. Thus, the greater the tendency of droplets to evaporate as a group, the lower is the correlation coefficient between droplet number density and local vapour mass fraction. Hence, it is possible that the same amount of vapour is generated even when the droplet number density increases five times (see figure 12). This happens due to presence of vapour from neighbouring droplets reducing the droplet evaporation rate.
$R_{n\ast y}$
(figure 13) for any droplet size class. Thus, the greater the tendency of droplets to evaporate as a group, the lower is the correlation coefficient between droplet number density and local vapour mass fraction. Hence, it is possible that the same amount of vapour is generated even when the droplet number density increases five times (see figure 12). This happens due to presence of vapour from neighbouring droplets reducing the droplet evaporation rate.
Now we discuss some factors which may possibly influence evaluation of the group evaporation number. As mentioned earlier, the thickness of the laser sheet is approximately 1 mm, which is approximately 25 times the average droplet size. Thus, droplets at different depths could have been imaged. Unfortunately, we could not verify the effect of reducing the laser sheet thickness on our results. However, there is reasonable doubt that this depth is the full 1 mm for the following reasons. First, the depth of focus was approximately 0.9 mm (for the PLIF camera setting), which is slightly less than the thickness of the laser sheet (1 mm). Hence, most of the droplets and vapour phase in the PLIF images are focused. Although the depth of focus for the ILIDS setting was approximately 0.2 mm, which is much smaller than the laser sheet thickness, in the ILIDS technique, the droplet images are deliberately defocused anyway. Second, we note that the laser sheet has a Gaussian intensity distribution, and instrument thresholds and validation criteria in the image processing will limit the ability to detect droplets far from the central maximum intensity of the laser sheet. (The validation criteria of the ILIDS reject some of the droplets that are at the edges of the laser sheet, which do not satisfy all the criteria. This has been explained in Zarogoulidis Reference Zarogoulidis2016.) The net result of all the above contributions is that the validated droplet images for the ILIDS technique are expected to be from a narrow central area of the laser sheet. The conclusion that the droplets that are close to the central plane of the laser sheet are measured is further justified by the fact that the length of recorded droplet fringe patterns does not vary significantly, which would have been the case if the droplets were imaged at different depths of the laser sheet. We would like to note that the above effect is expected not to be a limiting factor for measurement of vapour–droplet correlations (either droplet number density–vapour mass fraction or droplet velocity–vapour mass fraction correlations). This is because both droplet and vapour phases correspond to the same volume within the spray illuminated by the laser sheet. However, larger thickness of the laser sheet may lead to bias in relative position of the droplets since two droplets at different depths may appear closer in the images. Hence, this may lead to underestimation of the measured inter-droplet distance and thus some overestimation of the
![]() $G$
values. We have made an estimate of this for the worst possible scenario, where it is assumed that apart from radial separation between droplets, the separation in the direction of the depth of the laser sheet is also present and equal to the effective thickness of the laser sheet (equal to the
$G$
values. We have made an estimate of this for the worst possible scenario, where it is assumed that apart from radial separation between droplets, the separation in the direction of the depth of the laser sheet is also present and equal to the effective thickness of the laser sheet (equal to the
![]() $1/e^{2}$
distance). For such a case it is found that the approach followed in the paper results in overestimation of
$1/e^{2}$
distance). For such a case it is found that the approach followed in the paper results in overestimation of
![]() $G$
values by approximately 20–30 % (larger values for inner spray locations). However, the value of
$G$
values by approximately 20–30 % (larger values for inner spray locations). However, the value of
![]() $G$
is still of the order of ‘one’ close to the spray centre, indicating internal group evaporation.
$G$
is still of the order of ‘one’ close to the spray centre, indicating internal group evaporation.
In addition, it is noted here that the current estimation of the instantaneous value of
![]() $G$
uses some assumptions which are not compatible with the analytical expression for
$G$
uses some assumptions which are not compatible with the analytical expression for
![]() $G$
of Chiu & coworkers, which itself is based on the assumption of a quasi-steady and laminar process, constant droplet size and spacing, spherical symmetry, etc. Hence, some discrepancies between the experimental results and inference from theoretical analysis are found. In figure 22, some instantaneous values of
$G$
of Chiu & coworkers, which itself is based on the assumption of a quasi-steady and laminar process, constant droplet size and spacing, spherical symmetry, etc. Hence, some discrepancies between the experimental results and inference from theoretical analysis are found. In figure 22, some instantaneous values of
![]() $G$
exceed unity, implying external group evaporation (when individual droplet evaporation seizes to exist), which the theory suggests is not possible for the current measurement locations and flow conditions. In our case, the instantaneous droplet AMD and spatially averaged droplet spacing,
$G$
exceed unity, implying external group evaporation (when individual droplet evaporation seizes to exist), which the theory suggests is not possible for the current measurement locations and flow conditions. In our case, the instantaneous droplet AMD and spatially averaged droplet spacing,
![]() $l_{d}$
, in a droplet cluster were used to evaluate
$l_{d}$
, in a droplet cluster were used to evaluate
![]() $G$
, while within a ‘real’ droplet cluster formed due to the interaction with the flow turbulence, the size of the droplets is not the same and the inter-droplet distance is not uniform. In addition the value of
$G$
, while within a ‘real’ droplet cluster formed due to the interaction with the flow turbulence, the size of the droplets is not the same and the inter-droplet distance is not uniform. In addition the value of
![]() $G$
is affected by the droplet cluster length
$G$
is affected by the droplet cluster length
![]() $L_{c}$
, whose accurate determination is affected by the uncertainty and spatial resolution of the RDF measurement. However, the current results represent the first measurements of instantaneous values of
$L_{c}$
, whose accurate determination is affected by the uncertainty and spatial resolution of the RDF measurement. However, the current results represent the first measurements of instantaneous values of
![]() $G$
in evaporating sprays in a turbulent environment and can quantitatively elucidate the validity of group combustion theory, which only considers laminar flows without the presence of slip velocity between the droplet and air. The current results demonstrate that, despite the limiting assumptions of the group combustion theory, it provides reasonable assessment of the droplet group evaporation in sprays interacting with turbulent flows for the current conditions.
$G$
in evaporating sprays in a turbulent environment and can quantitatively elucidate the validity of group combustion theory, which only considers laminar flows without the presence of slip velocity between the droplet and air. The current results demonstrate that, despite the limiting assumptions of the group combustion theory, it provides reasonable assessment of the droplet group evaporation in sprays interacting with turbulent flows for the current conditions.
Finally, we would like to mention that we have not discussed the scope of comparison of our experimental results with computational modelling (this was not the purpose of our research). However, the measured correlations between vapour mass fraction and droplet number density and velocity provide a basis for evaluating existing models and developing new models for unclosed vaporization source terms appearing in the transport equations for mean and variance of vapour mass fraction, as we explained in the Introduction. Measurements of such correlations have not been available until this work.
4 Conclusions
The interaction of droplet dispersion and evaporation was studied in an acetone spray evaporating under ambient conditions of atmospheric pressure and temperature of
![]() $15\,^{\circ }\text{C}$
. The aim of the paper was to investigate the correlation between local vapour mass fraction and droplet number density and velocity, and, specifically, to study the role of gas-phase turbulence on such correlations. The emphasis was on the influence of droplet clusters on collective evaporation of droplet clouds within the spray. Unlike the studies based on evaporation of single droplets, where the gas turbulence always increases the rate of droplet evaporation, in sprays the turbulence has an indirect effect on the droplet evaporation rate due to formation of droplet clusters as a consequence of preferential segregation of partially responsive droplets to large scale eddies of gas-phase turbulence. Droplet clustering leads to reduction of the droplet evaporation rate due to closer spacing of the droplets.
$15\,^{\circ }\text{C}$
. The aim of the paper was to investigate the correlation between local vapour mass fraction and droplet number density and velocity, and, specifically, to study the role of gas-phase turbulence on such correlations. The emphasis was on the influence of droplet clusters on collective evaporation of droplet clouds within the spray. Unlike the studies based on evaporation of single droplets, where the gas turbulence always increases the rate of droplet evaporation, in sprays the turbulence has an indirect effect on the droplet evaporation rate due to formation of droplet clusters as a consequence of preferential segregation of partially responsive droplets to large scale eddies of gas-phase turbulence. Droplet clustering leads to reduction of the droplet evaporation rate due to closer spacing of the droplets.
A novel experimental technique of combining ILIDS with PLIF (Sahu et al.
Reference Sahu, Hardalupas and Taylor2014b
) was adopted for simultaneous planar characterization of droplet size, velocity and number density and vapour mass fraction around droplets in the evaporating spray. This facilitated measurement of some two-phase statistics, which are reported for the first time. The measurement locations were at 350 mm downstream from the exit of an air assist atomizer so that considerable mixing of droplet vapour and ambient air is expected. Two-phase measurements are reported for four different radial locations beginning from the spray axis up to the edge of the spray (
![]() $R=0$
, 15, 30 and 45 mm). Droplet measurements by ILIDS in a non-evaporating water spray under the same flow conditions were also obtained, which provided a reference to evaluate the effect of evaporation on droplet dispersion. The droplet Stokes numbers near the spray centre were of the order of 0.1 when based on energy-containing eddy time scales indicating good-to-partial response of droplets. The main findings of the research work are as follows.
$R=0$
, 15, 30 and 45 mm). Droplet measurements by ILIDS in a non-evaporating water spray under the same flow conditions were also obtained, which provided a reference to evaluate the effect of evaporation on droplet dispersion. The droplet Stokes numbers near the spray centre were of the order of 0.1 when based on energy-containing eddy time scales indicating good-to-partial response of droplets. The main findings of the research work are as follows.
(i) While the radial variation of mean quantities (SMD, average droplet number density and velocity, average vapour mass fraction) in the evaporative spray are as expected, some interesting results are obtained for the corresponding fluctuations of these quantities. The fluctuations of droplet velocity and number density and vapour mass fraction (relative to the respective mean) were found to increase towards the edge of the spray. However, for all measurement locations, these fluctuations were always higher for the evaporative spray in comparison to the water spray. For the acetone spray, evaporation significantly reduces the radial gradients of average droplet number density across the spray, though its influence on average droplet velocity was not significant.
(ii) In general, the local instantaneous vapour fraction (
 $Y_{F}$
) was found to be proportional to droplet number density (
$Y_{F}$
) was found to be proportional to droplet number density (
 $N$
) at that instant. The correlation between local fluctuations of droplet number density and vapour mass fraction (
$N$
) at that instant. The correlation between local fluctuations of droplet number density and vapour mass fraction (
 $R_{ny}$
) is relatively high (
$R_{ny}$
) is relatively high (
 ${\approx}0.5$
). This is attributed to good-to-partial response of droplets to large-scale eddies of the air flow and similar density of acetone vapour and air such that the vapour is advected with the air flow carrying the droplets. This is further supported by the measured correlation between local fluctuations of droplet velocity and vapour mass fraction (
${\approx}0.5$
). This is attributed to good-to-partial response of droplets to large-scale eddies of the air flow and similar density of acetone vapour and air such that the vapour is advected with the air flow carrying the droplets. This is further supported by the measured correlation between local fluctuations of droplet velocity and vapour mass fraction (
 $R_{nu}$
), which was approximately 0.6.
$R_{nu}$
), which was approximately 0.6.(iii) The probability distribution of the instantaneous droplet–gas slip velocity indicated that the mean slip velocity was close to zero, and consequently the droplet Reynolds number based on the mean slip velocity was very small (
 ${\approx}0.2$
). In addition, the vaporization Damköhler number (
${\approx}0.2$
). In addition, the vaporization Damköhler number (
 $Da_{v}$
) was approximately 1, which means the droplet evaporation time and characteristic time scale of large eddies are of the same order. Hence, the influence of mean slip velocity on droplet evaporation is not expected to be significant in comparison to the instantaneous fluctuations of slip velocity, which refers to the direct effect of turbulence. We find that the correlation,
$Da_{v}$
) was approximately 1, which means the droplet evaporation time and characteristic time scale of large eddies are of the same order. Hence, the influence of mean slip velocity on droplet evaporation is not expected to be significant in comparison to the instantaneous fluctuations of slip velocity, which refers to the direct effect of turbulence. We find that the correlation,
 $R_{ny}$
, is smaller when evaluated for a smaller size of the measurement window, which indicates that the instantaneous slip velocity influences the local spatial disparity between the droplet and vapour phases.
$R_{ny}$
, is smaller when evaluated for a smaller size of the measurement window, which indicates that the instantaneous slip velocity influences the local spatial disparity between the droplet and vapour phases.(iv) Some interesting observations are made from the scattering of data in the
 $Y_{F}$
versus
$Y_{F}$
versus
 $N$
plot: considerable variation in the local vapour mass fraction is possible even when the local droplet number density is the same; in other words, the same vapour mass fraction is measured when the local droplet number density is considerably different. This is attributed to droplet clustering, which leads to reduction in the evaporation rate of droplets. The measurement of the correlation coefficients between fluctuations of droplet number density of different size classes (
$N$
plot: considerable variation in the local vapour mass fraction is possible even when the local droplet number density is the same; in other words, the same vapour mass fraction is measured when the local droplet number density is considerably different. This is attributed to droplet clustering, which leads to reduction in the evaporation rate of droplets. The measurement of the correlation coefficients between fluctuations of droplet number density of different size classes (
 $R_{n\ast n}$
) as well as the radial distribution function (RDF) confirmed the presence of droplet clustering. Comparison of these statistical quantities between the water and the acetone spray indicated that droplet evaporation promoted droplet clustering in the spray. This also explains the results described in item (i).
$R_{n\ast n}$
) as well as the radial distribution function (RDF) confirmed the presence of droplet clustering. Comparison of these statistical quantities between the water and the acetone spray indicated that droplet evaporation promoted droplet clustering in the spray. This also explains the results described in item (i).(v) Finally, the group evaporation number (
 $G$
) was estimated at different measurement locations by estimating the length scale of droplet clusters measured from the RDF, and average droplet size and inter-droplet spacing for times corresponding to passage of droplet clusters through the measurement window. The magnitude of
$G$
) was estimated at different measurement locations by estimating the length scale of droplet clusters measured from the RDF, and average droplet size and inter-droplet spacing for times corresponding to passage of droplet clusters through the measurement window. The magnitude of
 $G$
(
$G$
(
 ${\approx}0.5$
–1) indicated not only that droplets evaporate individually but also that the ‘internal group evaporation’ mode is possible. This is in agreement with the earlier observations on droplet clustering and signifies that the droplets may evaporate in groups even far away from the injector exit. In addition, the large fluctuations in the magnitude of instantaneous values of
${\approx}0.5$
–1) indicated not only that droplets evaporate individually but also that the ‘internal group evaporation’ mode is possible. This is in agreement with the earlier observations on droplet clustering and signifies that the droplets may evaporate in groups even far away from the injector exit. In addition, the large fluctuations in the magnitude of instantaneous values of
 $G$
at all measurement locations implied temporal variations in the mode of droplet cloud evaporation.
$G$
at all measurement locations implied temporal variations in the mode of droplet cloud evaporation.These experiments provide an assessment, for the first time, of the validity of the group combustion theory in turbulent evaporative sprays, which are beyond the assumption of the theory.
Acknowledgements
The authors would like to acknowledge support from the Engineering and Physical Sciences Research Council (EPSRC) in the UK under grants GR/R34714/01and EP/G01597X/01 and European Union Framework 7 contract agreement 265848, entitled ‘Fuel Injector Research for Sustainable Transport (FIRST)’. Y.H. also acknowledges support from the Asian Office of Aerospace Research and Development (AOARD) through project FA2386-13-1-4065.