Hostname: page-component-cd9895bd7-gbm5v Total loading time: 0 Render date: 2024-12-23T18:10:39.908Z Has data issue: false hasContentIssue false
  • English
  • Français

Interaction of coherent flow structures in adverse pressure gradient turbulent boundary layers

Published online by Cambridge University Press:  24 June 2019

Matthew Bross Open the ORCID record for Matthew Bross [Opens in a new window] ,
Thomas Fuchs Open the ORCID record for Thomas Fuchs [Opens in a new window]  and
Christian J. Kähler
Matthew Bross*
Affiliation:
Institute of Fluid Mechanics and Aerodynamics, Universität der Bundeswehr München, 85577 Neubiberg, Germany
Thomas Fuchs
Affiliation:
Institute of Fluid Mechanics and Aerodynamics, Universität der Bundeswehr München, 85577 Neubiberg, Germany
Christian J. Kähler
Affiliation:
Institute of Fluid Mechanics and Aerodynamics, Universität der Bundeswehr München, 85577 Neubiberg, Germany
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

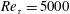With the aim to characterize the near-wall flow structures and their interaction with large-scale motions in the log-law region, time-resolved planar and volumetric flow field measurements were performed in the near-wall and log-law region of an adverse pressure gradient turbulent boundary layer following a zero pressure gradient turbulent boundary layer at a friction Reynolds number $Re_{\unicode[STIX]{x1D70F}}=5000$. Due to the high spatial and temporal resolution of the measurements, it was possible to resolve and identify uniform-momentum zones in the region 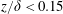$z/\unicode[STIX]{x1D6FF}<0.15$ or 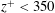$z^{+}<350$ and to relate them with well known coherent flow motions near the wall. The space–time results confirm that the turbulent superstructures have a strong impact even on the very near-wall flow motion and also their alternating appearance in time and intensity could be quantified over long time sequences. Using the time record of the velocity field, rare localized separation events appearing in the viscous sublayer were also analysed. By means of volumetric particle tracking velocimetry their three-dimensional topology and dynamics could be resolved. Based on the results, a conceptual model was deduced that explains their rare occurrence, topology and dynamics by means of a complex interaction process between low-momentum turbulent superstructures, near-wall low-speed streaks and tilted longitudinal and spanwise vortices located in the near-wall region.

JFM classification

Boundary Layers: Boundary layer structure Turbulent Flows: Turbulent boundary layers
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 873 , 25 August 2019 , pp. 287 - 321
Check for updates
Copyright
© 2019 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Adrian, R. J., Meinhart, C. D. & Tomkins, C. D. 2000 Vortex organization in the outer region of the turbulent boundary layer. J. Fluid Mech. 422, 1–54.Google Scholar
Baars, W. J., Hutchins, N. & Marusic, I. 2017 Reynolds number trend of hierarchies and scale interactions in turbulent boundary layers. Phil. Trans. R. Soc. Lond. A 375 (2089), 1–18.Google Scholar
Balakumar, B. J. & Adrian, R. J. 2007 Large- and very-large-scale motions in channel and boundary-layer flows. Phil. Trans. R. Soc. Lond. A 365 (1852), 665–681.Google Scholar
Bobke, A., Vinuesa, R., Örlü, R. & Schlatter, P. 2017 History effects and near equilibrium in adverse-pressure-gradient turbulent boundary layers. J. Fluid Mech. 820, 667–692.Google Scholar
Bross, M. & Kähler, C. J. 2016 Time-resolved 3D-PTV analysis of near wall reverse flow events in APG turbulent boundary layers. In 18th International Symposium on the App. of Laser and Imaging Tech. to Fluid Mech., July 4–7, Lisbon, Portugal.Google Scholar
Brücker, C. 2015 Evidence of rare backflow and skin-friction critical points in near-wall turbulence using micropillar imaging. Phys. Fluids 27 (3), 031705.Google Scholar
Buchmann, N.A., Cierpka, C., Knopp, T., Schanze, D., Schröder, A., Hain, R. & Kähler, C.J. 2014 Large scale adverse pressure gradient turbulent boundary layer investigation by means of PIV and PTV. In 17th International Symposium on the App. of Laser and Imaging Tech. to Fluid Mech., July 7–10, Lisbon, Portugal.Google Scholar
Buchmann, N. A., Kücükosman, Y. C., Ehrenfried, K. & Kähler, C. J. 2016 Wall pressure signature in compressible turbulent boundary layers. In Progress in Wall Turbulence 2, pp. 93–102. Springer International Publishing.Google Scholar
Cardesa, J. I., Monty, J., Soria, J. & Chong, M. 2014 Skin-friction critical points in wall-bounded flows. J. Phys. 506, 012009.Google Scholar
Chauhan, K. A., Monkewitz, P. A. & Hassan, H. N. 2009 Criteria for assessing experiments in zero pressure gradient boundary layers. Fluid Dyn. Res. 41 (2), 021404.Google Scholar
Chin, C., Vinuesa, R., Örlü, R., Cardesa, J.I., Noorani, A., Schlatter, P. & Chong, M.S. 2018 Flow topology of rare back flow events and critical points in turbulent channels and toroidal pipes. J. Phys. 1001, 012002.Google Scholar
Cierpka, C., Lütke, B. & Kähler, C. J. 2013a Higher order multi-frame particle tracking velocimetry. Exp. Fluids 54, 1533.Google Scholar
Cierpka, C., Scharnowski, S. & Kähler, C. J. 2013b Parallax correction for precise near-wall flow investigations using particle imaging. Appl. Opt. 52 (12), 2923–2931.Google Scholar
Diaz-Daniel, C., Laizet, S. & Vassilicos, J. C. 2017 Wall shear stress fluctuations: mixed scaling and their effects on velocity fluctuations in a turbulent boundary layer. Phys. Fluids 29 (5), 055102.Google Scholar
Fernholz, H. H. & Finley, P. J. 1996 The incompressible zero-pressure-gradient turbulent boundary layer: an assessment of the data. Prog. Aerosp. Sci. 32 (4), 245–311.Google Scholar
Fuchs, T., Bross, M., Scharnowski, S. & Kähler, C. J. 2018 Parallax corrected PTV for precise near wall boundary layer measurements. In 19th International Symposium on the App. of Laser and Imaging Tech. to Fluid Mech., July 16–19, Lisbon, Portugal.Google Scholar
Fuchs, T., Hain, R. & Kähler, C. J. 2016a Double-frame 3D-PTV using a tomographic predictor. Exp. Fluids 57, 174.Google Scholar
Fuchs, T., Hain, R. & Kähler, C. J. 2016b Uncertainty quantification of three-dimensional velocimetry techniques for small measurement depths. Exp. Fluids 57, 73.Google Scholar
Fuchs, T., Hain, R. & Kähler, C. J. 2017 Non-iterative double-frame 2D/3D particle tracking velocimetry. Exp. Fluids 58, 119.Google Scholar
Ganapathisubramani, B., Hutchins, N., Hambleton, W. T., Longmire, E. K. & Marusic, I. 2005 Investigation of large-scale coherence in a turbulent boundary layer using two-point correlations. J. Fluid Mech. 524, 57–80.Google Scholar
Ganapathisubramani, B., Hutchins, N., Monty, J. P., Chung, D. & Marusic, I. 2012 Amplitude and frequency modulation in wall turbulence. J. Fluid Mech. 712, 61–91.Google Scholar
Harun, Z., Monty, J. P., Mathis, R. & Marusic, I. 2013 Pressure gradient effects on the large-scale structure of turbulent boundary layers. J. Fluid Mech. 715, 477–498.Google Scholar
Hutchins, N. & Marusic, I. 2007a Evidence of very long meandering features in the logarithmic region of turbulent boundary layers. J. Fluid Mech. 579, 1–29.Google Scholar
Hutchins, N. & Marusic, I. 2007b Large-scale influences in near-wall turbulence. Phil. Trans. R. Soc. Lond. A 365, 647–664.Google Scholar
Hutchins, N., Monty, J. P., Ganapathisubramani, B., NG, H. C. H. & Marusic, I. 2011 Three-dimensional conditional structure of a high-Reynolds-number turbulent boundary layer. J. Fluid Mech. 673, 255–285.Google Scholar
Hutchins, N., Nickels, T. B., Marusic, I. & Chong, M. S. 2009 Hot-wire spatial resolution issues in wall-bounded turbulence. J. Fluid Mech. 635, 103–136.Google Scholar
Jalalabadi, R. & Sung, H. J. 2018 Influence of backflow on skin friction in turbulent pipe flow. Phys. Fluids 30 (6), 065104.Google Scholar
Jiménez, J., Del Álamo, J. C. & Flores, O. 2004 The large-scale dynamics of near-wall turbulence. J. Fluid Mech. 505, 179–199.Google Scholar
Kähler, C. J., Astarita, T., Vlachos, P., Sakakibara, J., Hain, R., Discetti, S., La Foy, R. & Cierpka, C. 2016 Main results of the 4th international PIV challenge. Exp. Fluids 57, 97.Google Scholar
Kähler, C. J., Sammler, B. & Kompenhans, J. 2002 Generation and control of tracer particles for optical flow investigations in air. Exp. Fluids 33, 736.Google Scholar
Kähler, C. J., Scharnowski, S. & Cierpka, C. 2012a On the resolution limit of digital particle image velocimetry. Exp. Fluids 52, 1629.Google Scholar
Kähler, C. J., Scharnowski, S. & Cierpka, C. 2012b On the uncertainty of digital PIV and PTV near walls. Exp. Fluids 52, 1641.Google Scholar
Kitsios, V., Sekimoto, A., Atkinson, C., Sillero, J. A., Borrell, G., Gungor, A. G., Jiménez, J. & Soria, J. 2017 Direct numerical simulation of a self-similar adverse pressure gradient turbulent boundary layer at the verge of separation. J. Fluid Mech. 829, 392–419.Google Scholar
Klebanoff, P. S.1955 Characteristics of turbulence in a boundary layer with zero pressure gradient. NASA Tech. Rep. 1247 available from NASA, Washington, D.C.Google Scholar
Kline, S. J., Reynolds, W. C., Schraub, F. A. & Runstadler, P. W. 1967 The structure of turbulent boundary layers. J. Fluid Mech. 30, 741–773.Google Scholar
Knopp, T., Buchmann, N. A., Schanz, D., Eisfeld, B., Cierpka, C., Hain, R., Schröder, A. & Kähler, C. J. 2015 Investigation of scaling laws in a turbulent boundary layer flow with adverse pressure gradient using PIV. J. Turbul. 16 (3), 250–272.Google Scholar
Kovasznay, L. S. G., Kibens, V. & Blackwelder, R. F. 1970 Large-scale motion in the intermittent region of a turbulent boundary layer. J. Fluid Mech. 41 (2), 283–325.Google Scholar
Laskari, A., de Kat, R., Hearst, R. J. & Ganapathisubramani, B. 2018 Time evolution of uniform momentum zones in a turbulent boundary layer. J. Fluid Mech. 842, 554–590.Google Scholar
Lenaers, P., Li, Q., Brethouwer, G., Schlatter, P. & Örlü, R. 2012 Rare backflow and extreme wall-normal velocity fluctuations in near-wall turbulence. Phys. Fluids 24 (3), 035110.Google Scholar
Lin, J., Laval, J. P., Foucaut, J. M. & Stanislas, M. 2008 Quantitative characterization of coherent structures in the buffer layer of near-wall turbulence. Part 1. Streaks. Exp. Fluids 45, 999.Google Scholar
Maciel, Y., Wei, T., Gungor, A. G. & Simens, M. P. 2018 Outer scales and parameters of adverse-pressure-gradient turbulent boundary layers. J. Fluid Mech. 844, 5–35.Google Scholar
Marusic, I. & Heuer, W. D. C. 2007 Reynolds number invariance of the structure inclination angle in wall turbulence. Phys. Rev. Lett. 99, 114504.Google Scholar
Mathis, R., Hutchins, N. & Marusic, I. 2009 Large scale amplitude modulation of the small scale structures in turbulent boundary layers. J. Fluid Mech. 628, 311–337.Google Scholar
Meinhart, C. D. & Adrian, R. J. 1995 On the existence of uniform momentum zones in a turbulent boundary layer. Phys. Fluids 7, 694–696.Google Scholar
Michael, M. & Rainer, F. 2002 DNS of a turbulent boundary layer with separation. Intl J. Heat Fluid Flow 23 (5), 572–581.Google Scholar
Monty, J. P., Harun, Z. & Marusic, I. 2011 A parametric study of adverse pressure gradient turbulent boundary layers. Intl J. Heat Fluid Flow 32, 575–585.Google Scholar
Monty, J. P., Hutchins, N., NG, H. C. H., Marusic, I. & Chong, M. S. 2009 A comparison of turbulent pipe, channel and boundary layer flows. J. Fluid Mech. 632, 431–442.Google Scholar
Novara, M., Schanz, D., Reuther, N., Kähler, C. J. & Schröder, A. 2016 Lagrangian 3D particle tracking in high-speed flows: Shake-The-Box for multi-pulse systems. Exp. Fluids 57, 128.Google Scholar
Raffel, M., Willert, C., Scarano, F., Kähler, C. J., Wereley, S. T. & Kompenhans, J. 2018 Particle Image Velocimetry. A Practical Guide. Springer.Google Scholar
Rao, K., Narasimha, R. & Narayanan, M. 1971 The ‘bursting’ phenomenon in a turbulent boundary layer. J. Fluid Mech. 48, 339–352.Google Scholar
Reuther, N. & Kähler, C. J. 2018 Evaluation of large-scale turbulent/non-turbulent interface detection methods for wall-bounded flows. Exp. Fluids 59, 121.Google Scholar
Reuther, N., Scharnowski, S., Hain, R., Schanz, D., Schröder, A. & Kähler, C. J. 2015 Experimental investigation of adverse pressure gradient turbulent boundary layers by means of large-scale PIV. In 11th International Symposium on PIV, September 14–16, Santa Barbara, USA.Google Scholar
Samie, M., Marusic, I., Hutchins, N., Fu, M. K., Fan, Y., Hultmark, M. & Smits, A. J. 2018 Fully resolved measurements of turbulent boundary layer flows up to Re 𝜏 = 20 000. J. Fluid Mech. 851, 391–415.Google Scholar
Saxton-Fox, T. & McKeon, B. J. 2017 Coherent structures, uniform momentum zones and the streamwise energy spectrum in wall-bounded turbulent flows. J. Fluid Mech. 826, R6.Google Scholar
Schanz, D., Gesemann, S. & Schröder, A. 2016 Shake-The-Box: Lagrangian particle tracking at high particle image densities. Exp. Fluids 57, 70.Google Scholar
Scharnowski, S. & Kähler, C. J. 2012 On the effect of curved streamlines on the accuracy of PIV vector fields. Exp. Fluids 54, 1435.Google Scholar
Schröder, A., Schanz, D., Geisler, R. & Gesemann, S. 2016 Investigations of coherent structures in near-wall turbulence and large wall-shear stress events using Shake-The-Box. In 18th International Symposium on the App. of Laser and Imaging Tech. to F. Mech., July 4–7, Lisbon, Portugal.Google Scholar
Sillero, J. A., Jiménez, J. & Moser, R. D. 2013 One-point statistics for turbulent wall-bounded flows at Reynolds numbers up to 𝛿+ ≈ 2000. Phys. Fluids 25 (10), 105102.Google Scholar
de Silva, C. M., Hutchins, N. & Marusic, I. 2016 Uniform momentum zones in turbulent boundary layers. J. Fluid Mech. 786, 309–331.Google Scholar
de Silva, C. M., Philip, J., Hutchins, N. & Marusic, I. 2017 Interfaces of uniform momentum zones in turbulent boundary layers. J. Fluid Mech. 820, 451–478.Google Scholar
Simpson, R. L. 1989 Turbulent boundary layer seperation. Annu. Rev. Fluid Mech. 21, 205–234.Google Scholar
Skåre, P. & Krogstad, P. 1994 A turbulent equilibrium boundary layer near separation. J. Fluid Mech. 272, 319–348.Google Scholar
Smith, C. R. & Metzler, S. P. 1983 The characteristics of low-speed streaks in the near-wall region of a turbulent boundary layer. J. Fluid Mech. 129, 27–54.Google Scholar
Spalart, P. R. & Coleman, G. N. 1997 Numerical study of separation bubble with heat transfer. Eur. J. Mech. (B/Fluids) 16, 169–187.Google Scholar
Vallikivi, M., Hultmark, M. & Smits, A. J. 2015 Turbulent boundary layer statistics at very high Reynolds number. J. Fluid Mech. 779, 371–389.Google Scholar
Vinuesa, R., Hosseini, S. M., Hanifi, A., Henningson, D. S. & Schlatter, P. 2017a Pressure-gradient turbulent boundary layers developing around a wing section. Flow Turbul. Combust. 99 (3), 613–641.Google Scholar
Vinuesa, R., Örlü, R. & Schlatter, P. 2017b Characterisation of backflow events over a wing section. J. Turbul. 18, 170–185.Google Scholar
Wallace, J. M. 2012 Highlights from 50 years of turbulent boundary layer research. J. Turbul. 13, 1–70.Google Scholar
Wallace, J. M. 2014 Space–time correlations in turbulent flow: a review. Theor. Appl. Mech. Lett. 4 (2), 022003.Google Scholar
Willert, C. E. 2015 High-speed particle image velocimetry for the efficient measurement of turbulence statistics. Exp. Fluids 56, 17.Google Scholar
Willert, C. E., Cuvier, C., Foucaut, J. M., Klinner, J., Stanislas, M., Laval, J. P., Srinath, S., Soria, J., Amili, O., Atkinson, C. et al. 2018 Experimental evidence of near-wall reverse flow events in a zero pressure gradient turbulent boundary layer. Exp. Therm. Fluid Sci. 91, 320–328.Google Scholar

Bross et al. supplementary movie 1

Uniform momentum zone time series in the near-wall region.

Download Bross et al. supplementary movie 1(Video)
Video 7.9 MB

Bross et al. supplementary movie 2

Three-dimensional trajectories below z+< 9 colored with u velocity component. Reverse flow is indicated in light purple shading.

Download Bross et al. supplementary movie 2(Video)
Video 10.2 MB