Article contents
Interaction between feedback aeroacoustic and acoustic resonance mechanisms in a cavity flow: a global stability analysis
Published online by Cambridge University Press: 01 February 2013
Abstract
We perform a global stability analysis of a flow over an open cavity, characterized by a Reynolds number, based on the upstream velocity and the cavity length, of 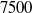 $7500$. We compute base flows and unstable global modes of the flow for different Mach numbers ranging from
$7500$. We compute base flows and unstable global modes of the flow for different Mach numbers ranging from 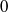 $0$ to
$0$ to 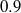 $0. 9$. In the incompressible regime (
$0. 9$. In the incompressible regime (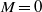 $M= 0$), we show that the flow is subject to global instabilities due to Kelvin–Helmholtz instabilities in the shear layer, which become strengthened by a hydrodynamic pressure feedback. The influence of the boundary-layer thickness and of the length-to-depth ratio of the cavity on these shear-layer modes has been investigated. In the compressible regime (
$M= 0$), we show that the flow is subject to global instabilities due to Kelvin–Helmholtz instabilities in the shear layer, which become strengthened by a hydrodynamic pressure feedback. The influence of the boundary-layer thickness and of the length-to-depth ratio of the cavity on these shear-layer modes has been investigated. In the compressible regime (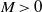 $M\gt 0$), we have shown that all unstable global modes are continuously connected to the incompressible shear-layer modes as
$M\gt 0$), we have shown that all unstable global modes are continuously connected to the incompressible shear-layer modes as 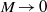 $M\rightarrow 0$. These shear-layer modes correspond to the beginning of branches of global modes, whose frequencies evolve (as a function of the Mach number), in accordance with the feedback aeroacoustic mechanism (Rossiter, Tech. Rep. Aero. Res. Counc. R. & M., 1964). We have also identified branches of global modes behaving in agreement with acoustic resonance mechanisms (East, J. Sound Vib., vol. 3, 1966, pp. 277–287; Tam, J. Sound Vib., vol. 49, 1976, pp. 353–364; Koch, AIAA J., vol. 43, 2005, pp. 2342–2349). At the intersections between both types of branches, the growth rate of the global modes is seen to display a local maximum. Along the aeroacoustic feedback branches, the number of vortical structures in the shear layer is kept constant, while the pressure pattern inside the cavity is conserved along the acoustic resonance branches. We show that both the feedback aeroacoustic and acoustic resonance mechanisms are at play over the entire subsonic regime, from
$M\rightarrow 0$. These shear-layer modes correspond to the beginning of branches of global modes, whose frequencies evolve (as a function of the Mach number), in accordance with the feedback aeroacoustic mechanism (Rossiter, Tech. Rep. Aero. Res. Counc. R. & M., 1964). We have also identified branches of global modes behaving in agreement with acoustic resonance mechanisms (East, J. Sound Vib., vol. 3, 1966, pp. 277–287; Tam, J. Sound Vib., vol. 49, 1976, pp. 353–364; Koch, AIAA J., vol. 43, 2005, pp. 2342–2349). At the intersections between both types of branches, the growth rate of the global modes is seen to display a local maximum. Along the aeroacoustic feedback branches, the number of vortical structures in the shear layer is kept constant, while the pressure pattern inside the cavity is conserved along the acoustic resonance branches. We show that both the feedback aeroacoustic and acoustic resonance mechanisms are at play over the entire subsonic regime, from 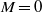 $M= 0$ to
$M= 0$ to 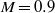 $M= 0. 9$. At low Mach numbers, we suggest that it is still the feedback aeroacoustic mechanism that selects the frequency, even though the fundamental acoustic resonance mode is also important due to enhancing the response. At higher Mach numbers, we observe that the pressure pattern of the acoustic resonance modes (fundamental acoustic modes, first longitudinal acoustic modes, first longitudinal-depth acoustic modes) inside the cavity determines the directivity of the radiated noise. Links with experimental results are finally discussed.
$M= 0. 9$. At low Mach numbers, we suggest that it is still the feedback aeroacoustic mechanism that selects the frequency, even though the fundamental acoustic resonance mode is also important due to enhancing the response. At higher Mach numbers, we observe that the pressure pattern of the acoustic resonance modes (fundamental acoustic modes, first longitudinal acoustic modes, first longitudinal-depth acoustic modes) inside the cavity determines the directivity of the radiated noise. Links with experimental results are finally discussed.
JFM classification
- Type
- Papers
- Information
- Copyright
- ©2013 Cambridge University Press
References
Yamouni et al. supplementary movie
Movie of iso-contours of pressure evolving in time over 3 time-periods for the mode 4a (σ=1.46, St=2.07)
- 76
- Cited by


