Hostname: page-component-78c5997874-lj6df Total loading time: 0 Render date: 2024-11-05T06:39:33.514Z Has data issue: false hasContentIssue false
  • English
  • Français

Instability of a boundary layer flow on a vertical wall in a stably stratified fluid

Published online by Cambridge University Press:  14 April 2016

Jun Chen ,
Yang Bai  and
Stéphane Le Dizès
Jun Chen
Affiliation:
Aix Marseille Université, CNRS, Centrale Marseille, IRPHE, UMR 7342, Marseille, F-13013, France
Yang Bai
Affiliation:
Aix Marseille Université, CNRS, Centrale Marseille, IRPHE, UMR 7342, Marseille, F-13013, France Université du Havre, CNRS, LOMC, UMR 6294, Le Havre, F-76058, France
Stéphane Le Dizès*
Affiliation:
Aix Marseille Université, CNRS, Centrale Marseille, IRPHE, UMR 7342, Marseille, F-13013, France
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The stability of a horizontal boundary layer flow on a vertical wall in a viscous stably stratified fluid is considered in this work. A temporal stability analysis is performed for a tanh velocity profile as a function of the Reynolds number 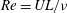$Re=UL/{\it\nu}$ and the Froude number 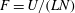$F=U/(LN)$ where 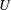$U$ is the main stream velocity, 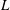$L$ the boundary layer thickness, 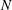$N$ the buoyancy frequency and ${\it\nu}$ the kinematic viscosity. The diffusion of density is neglected. The boundary layer flow is found to be unstable with respect to two instabilities. The first one is the classical viscous instability which gives rise to Tollmien–Schlichting (TS) waves. We demonstrate that, even in the presence of stratification, the most unstable TS wave remains two-dimensional and therefore independent of the Froude number. The other instability is three-dimensional, inviscid in nature and associated with the stratification. It corresponds to the so-called radiative instability. We show that this instability appears first for 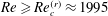$Re\geqslant Re_{c}^{(r)}\approx 1995$ for a Froude number close to 1.5 whereas the viscous instability develops for 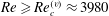$Re\geqslant Re_{c}^{(v)}\approx 3980$. For large Reynolds numbers, the radiative instability is also shown to exhibit a much larger growth rate than the viscous instability in a large Froude number interval. We argue that this instability could develop in experimental facilities as well as in geophysical situations encountered in ocean and atmosphere.

JFM classification

Boundary Layers: Boundary layer stability Geophysical and Geological Flows: Stratified flows
Type
Papers
Information
Journal of Fluid Mechanics , Volume 795 , 25 May 2016 , pp. 262 - 277
Check for updates
Copyright
© 2016 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Alford, M. H. & Gregg, M. C. 2006 Structure, propagation, and mixing of energetic baroclinic tides in Mamala Bay, Oahu, Hawaii. J. Phys. Oceanogr. 36, 997–1018.Google Scholar
Balmforth, N. J. 1999 Shear instability in shallow water. J. Fluid Mech. 387, 97–127.CrossRefGoogle Scholar
Betchov, R. & Criminale, W. O. 1967 Stability of Parallel Flows. Academic.Google Scholar
Candelier, J., Le Dizès, S. & Millet, C. 2011 Shear instability in a stratified fluid when shear and stratification are not aligned. J. Fluid Mech. 685, 191–201.Google Scholar
Candelier, J., Le Dizès, S. & Millet, C. 2012 Inviscid instability of a stably stratified compressible boundary layer on an inclined surface. J. Fluid Mech. 694, 524–539.CrossRefGoogle Scholar
Churilov, S. M. 2005 Stability analysis of stratified shear flows with a monotonic velocity profile without inflection points. J. Fluid Mech. 539, 25–55.Google Scholar
Churilov, S. M. 2008 Stability analysis of stratified shear flows with a monotonic velocity profile without inflection points. Part 2. Continuous density variation. J. Fluid Mech. 617, 301–326.Google Scholar
Drazin, P. G. & Reid, W. H. 1981 Hydrodynamic Stability. Cambridge University Press.Google Scholar
Frehlich, R., Meillier, Y. & Jensen, M. L. 2008 Measurements of boundary layer profiles with in situ sensors and doppler lidar. J. Atmos. Ocean. Technol. 25 (8), 1328–1340.CrossRefGoogle Scholar
Grimshaw, R. H. J. 1979 O n resonant over-reflexion of internal gravity waves from a Helmholtz velocity profile. J. Fluid Mech. 90, 161–178.Google Scholar
Howard, L. N. 1961 Note on a paper of John W. Miles. J. Fluid Mech. 10 (04), 509–512.Google Scholar
Kopev, V. F. & Leontev, E. A. 1983 A coustic instability of a axial vortex. Sov. Phys. Acoust. 29, 111–115.Google Scholar
Le Dizès, S. & Billant, P. 2009 Radiative instability in stratified vortices. Phys. Fluids 21 (9), 096602.Google Scholar
Lindzen, R. S. & Barker, J. W. 1985 Instability and wave over-reflection in stably stratified shear flow. J. Fluid Mech. 151, 189–217.Google Scholar
Mack, L. M. 1990 On the inviscid acoustic-mode instability of supersonic shear flows. Part 1: two-dimensional waves. Theor. Comput. Fluid Dyn. 2, 97–123.Google Scholar
Mahrt, L. 2014 Stably stratified atmospheric boundary layers. Annu. Rev. Fluid Mech. 46, 23–45.CrossRefGoogle Scholar
Mcintyre, M. E. & Weissman, M. A. 1978 On radiative instabilities and resonant overreflection. J. Atmos. Sci. 35, 1190–1196.Google Scholar
Miles, J. W. 1961 On the stability of heterogeneous shear flows. J. Fluid Mech. 10, 496–508.Google Scholar
Ohya, Y. & Uchida, T. 2003 Turbulence structure of stable boundary layers with a near-linear temperature profile. Boundary-Layer Met. 108, 19–38.Google Scholar
Paci, A., Knigge, C., Etling, D., Johnson, T., Esler, G. & Cazin, S. 2011 Topographic internal waves in the laboratory: two recent experiments carried in the CNRM-GAME stratified water tank. Geophys. Res. Abstracts 13, EGU2011–10299–2.Google Scholar
Parras, L. & Le Dizès, S. 2010 Temporal instability modes of supersonic round jets. J. Fluid Mech. 662, 173–196.Google Scholar
Plougonven, R. & Zeitlin, V. 2002 Internal gravity wave emission from a pancake vortex : an example of wave-vortex interaction in strongly stratified flows. Phys. Fluids 14, 1259–1268.Google Scholar
Riedinger, X. & Gilbert, A. D. 2014 Critical layer and radiative instabilities in shallow-water shear flows. J. Fluid Mech. 751, 539–569.Google Scholar
Riedinger, X., Le Dizès, S. & Meunier, P. 2010 Viscous stability properties of a Lamb–Oseen vortex in a stratified fluid. J. Fluid Mech. 645, 255–278.Google Scholar
Riedinger, X., Le Dizès, S. & Meunier, P. 2011 Radiative instability of the flow around a rotating cylinder in a stratified fluid. J. Fluid Mech. 672, 130–146.Google Scholar
Satomura, T. 1981 An investigation of shear instability in a shallow water. J. Met. Soc. Japan 59 (1), 148–167.Google Scholar
Wu, X. & Zhang, J. 2008a Instability of a stratified boundary layer and its coupling with internal gravity waves. Part 1. Linear and nonlinear instabilities. J. Fluid Mech. 595, 379–408.Google Scholar
Wu, X. & Zhang, J. 2008b Instability of a stratified boundary layer and its coupling with internal gravity waves. Part 2. Coupling with internal gravity waves via topography. J. Fluid Mech. 595, 409–433.Google Scholar