Hostname: page-component-78c5997874-j824f Total loading time: 0 Render date: 2024-11-17T03:24:26.131Z Has data issue: false hasContentIssue false
  • English
  • Français

Instability and cross-boundary-layer transport by shoaling internal waves over realistic slopes

Published online by Cambridge University Press:  22 May 2020

Chengzhu Xu Open the ORCID record for Chengzhu Xu [Opens in a new window]  and
Marek Stastna
Chengzhu Xu*
Affiliation:
Department of Civil Engineering, University of Calgary, Calgary, AB T2N 1N4, Canada
Marek Stastna
Affiliation:
Department of Applied Mathematics, University of Waterloo, Waterloo, ON N2L 3G1, Canada
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

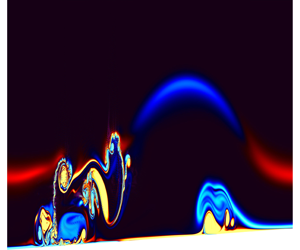
Internal solitary and solitary-like waves (ISW) play an important role in mixing and sediment resuspension in naturally occurring stratified fluids, primarily through various instabilities and wave-breaking mechanisms. When shoaling into shallow waters, waves of depression may either fission into a packet of waves of elevation over mild slopes or break over steep slopes. The fissioning process is generally considered a less efficient transport and resuspension mechanism, compared to wave breaking, since very little turbulent mixing or energy dissipation occurs during this process. In the present work, however, we found that this is not always the case, at least in the particular context of ISW boundary-layer interaction. Using high-resolution numerical simulations performed in a domain representing a tilted laboratory tank, we found that boundary-layer instability in the form of a separation bubble consistently occurs during the fissioning process. The separation bubble is generated beneath the wave of elevation that emerges from the fissioning process, and is vitally influenced by currents induced by the leading wave of depression. As the waves shoal further, the growth and breakdown of the separation bubble leads to significant cross-boundary-layer transport. The results suggest that the fissioning process, which occurs over a considerable geographical region in the ocean, can be as efficient as wave breaking when it comes to cross-boundary-layer transport.

JFM classification

Geophysical and Geological Flows: Internal waves Boundary Layers: Boundary layer separation Geophysical and Geological Flows: Sediment transport
Type
JFM Rapids
Information
Journal of Fluid Mechanics , Volume 895 , 25 July 2020 , R6
Copyright
© The Author(s), 2020. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Aghsaee, P., Boegman, L., Diamessis, P. J. & Lamb, K. G. 2012 Boundary-layer-separation-driven vortex shedding beneath internal solitary waves of depression. J. Fluid Mech. 690, 321–344.CrossRefGoogle Scholar
Aghsaee, P., Boegman, L. & Lamb, K. G. 2010 Breaking of shoaling internal solitary waves. J. Fluid Mech. 659, 289–317.CrossRefGoogle Scholar
Arthur, R. S. & Fringer, O. B. 2014 The dynamics of breaking internal solitary waves on slopes. J. Fluid Mech. 761, 360–398.CrossRefGoogle Scholar
Boegman, L. & Stastna, M. 2019 Sediment resuspension and transport by internal solitary waves. Annu. Rev. Fluid Mech. 51, 129–154.CrossRefGoogle Scholar
Carr, M. & Davies, P. A. 2010 Boundary layer flow beneath an internal solitary wave of elevation. Phys. Fluids 22, 026601.CrossRefGoogle Scholar
Carr, M., Franklin, J., King, S. E., Davies, P. A., Grue, J. & Dritschel, D. G. 2017 The characteristics of billows generated by internal solitary waves. J. Fluid Mech. 812, 541–577.CrossRefGoogle Scholar
Diamessis, P. J. & Redekopp, L. G. 2006 Numerical investigation of solitary internal wave-induced global instability in shallow water benthic boundary layers. J. Phys. Oceanogr. 36, 784–812.CrossRefGoogle Scholar
Duda, T. F., Lynch, J. F., Irish, J. D., Beardsley, R. C., Ramp, S. R., Chiu, C.-S., Tang, T. Y. & Yang, Y.-J. 2004 Internal tide and nonlinear wave behavior in the continental slope in the northern South China Sea. IEEE J. Ocean. Engng 29, 1105–1131.CrossRefGoogle Scholar
Farmer, D. M., Alford, M. H., Lien, R.-C., Yang, Y. J., Chang, M.-H. & Li, Q. 2011 From Luzon strait to Dongsha Plateau: stages in the life of an internal wave. Oceanography 24 (4), 64–77.CrossRefGoogle Scholar
Helfrich, K. R. & Melville, W. K. 2006 Long nonlinear internal waves. Annu. Rev. Fluid Mech. 38, 395–425.CrossRefGoogle Scholar
Kundu, P. K., Cohen, I. M. & Dowling, D. R. 2012 Fluid Mechanics, 5th edn. Academic Press.Google Scholar
Lamb, K. G. 2013 Internal wave breaking and dissipation mechanisms on the continental slope/shelf. Annu. Rev. Fluid Mech. 46, 231–254.CrossRefGoogle Scholar
Lamb, K. G. & Warn-Varnas, A. 2015 Two-dimensional numerical simulations of shoaling internal solitary waves at the ASIAEX site in the South China Sea. Nonlinear Process. Geophys. 22, 289–312.CrossRefGoogle Scholar
Orr, M. H. & Mignerey, P. C. 2003 Nonlinear internal waves in the South China Sea: observation of the conversion of depression internal waves to elevation internal waves. J. Geophys. Res. 108 (C3), 3064.CrossRefGoogle Scholar
Shroyer, E. L., Moum, J. N. & Nash, J. D. 2009 Observations of polarity reversal in shoaling nonlinear internal waves. J. Phys. Oceanogr. 39, 691–701.CrossRefGoogle Scholar
Stastna, M. & Lamb, K. G. 2008 Sediment resuspension mechanisms associated with internal waves in coastal waters. J. Geophys. Res. 113, C10016.CrossRefGoogle Scholar
Subich, C. J., Lamb, K. G. & Stastna, M. 2013 Simulation of the Navier–Stokes equations in the three dimensions with a spectral collocation method. Intl J. Numer. Mech. Fluids 73, 103–129.CrossRefGoogle Scholar
Sutherland, B. R., Barrett, K. J. & Ivey, G. N. 2013 Shoaling internal solitary waves. J. Geophys. Res. 118, 4111–4124.CrossRefGoogle Scholar
Trefethen, L. N. 2000 Spectral Methods in Matlab. Society for Industrial and Applied Mathematics.CrossRefGoogle Scholar