Hostname: page-component-586b7cd67f-t8hqh Total loading time: 0 Render date: 2024-11-22T18:01:00.608Z Has data issue: false hasContentIssue false
  • English
  • Français

Instabilities and sensitivities in a flow over a rotationally flexible cylinder with a rigid splitter plate

Published online by Cambridge University Press:  06 October 2021

R.L.G. Basso ,
Y. Hwang Open the ORCID record for Y. Hwang [Opens in a new window] ,
G.R.S. Assi Open the ORCID record for G.R.S. Assi [Opens in a new window]  and
S.J. Sherwin Open the ORCID record for S.J. Sherwin [Opens in a new window]
R.L.G. Basso
Affiliation:
Department of Aeronautics, Imperial College London, South Kensington SW7 2AZ, UK Department of Naval Architecture and Ocean Engineering, University of São Paulo, Brazil
Y. Hwang*
Affiliation:
Department of Aeronautics, Imperial College London, South Kensington SW7 2AZ, UK
G.R.S. Assi
Affiliation:
Department of Naval Architecture and Ocean Engineering, University of São Paulo, Brazil
S.J. Sherwin
Affiliation:
Department of Aeronautics, Imperial College London, South Kensington SW7 2AZ, UK
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

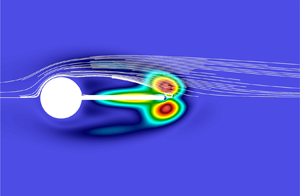
This paper investigates the origin of flow-induced instabilities and their sensitivities in a flow over a rotationally flexible circular cylinder with a rigid splitter plate. A linear stability and sensitivity problem is formulated in the Eulerian frame by considering the geometric nonlinearity arising from the rotational motion of the cylinder which is not present in the stationary or purely translating stability methodology. This nonlinearity needs careful and consistent treatment in the linearised problem particularly when considering the Eulerian frame or reference adopted in this study that is not so widely considered. Two types of instabilities arising from the fluid–structure interaction are found. The first type of instabilities is the stationary symmetry breaking mode, which was well reported in previous studies. This instability exhibits a strong correlation with the length of the recirculation zone. A detailed analysis of the instability mode and its sensitivity reveals the importance of the flow near the tip region of the plate for the generation and control of this instability mode. The second type is an oscillatory torsional flapping mode, which has not been well reported. This instability typically emerges when the length of the splitter plate is sufficiently long. Unlike the symmetry breaking mode, it is not so closely correlated with the length of the recirculation zone. The sensitivity analysis however also reveals the crucial role played by the flow near the tip region in this instability. Finally, it is found that many physical features of this instability are reminiscent of those of the flapping (or flutter instability) observed in a flow over a flexible plate or a flag, suggesting that these instabilities share the same physical origin.

JFM classification

Flow Control: Instability control Aerodynamics: Flow-structure interactions
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 928 , 10 December 2021 , A24
Check for updates
Copyright
© The Author(s), 2021. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Akervik, E., Brandt, L., Henningson, D.S., Hoepffner, J., Marxen, O. & Schlatter, P. 2006 Steady solutions of the Navier–Stokes equations by selective frequency damping. Phys. Fluids 18 (6), 068102.CrossRefGoogle Scholar
Anderson, E.A. & Szewczyk, A.A. 1997 Effects of a splitter plate on the near wake of a circular cylinder in 2 and 3-dimensional flow configurations. Exp. Fluids 23 (2), 161–174.CrossRefGoogle Scholar
Assi, G.R.S., Bearman, P.W. & Kitney, N. 2009 Low drag solutions for suppressing vortex-induced vibration of circular cylinders. J. Fluids Struct. 25 (4), 666–675.CrossRefGoogle Scholar
Assi, G.R.S., Bearman, P.W., Kitney, N. & Tognarelli, M.A. 2010 Suppression of wake-induced vibration of tandem cylinders with free-to-rotate control plates. J. Fluids Struct. 26, 1045–1057.CrossRefGoogle Scholar
Assi, G.R.S., Bearman, P.W. & Tognarelli, M.A. 2014 a On the stability of a free-to-rotate short-tail fairing and a splitter plate as suppressors of vortex-induced vibration. Ocean Engng 92, 234–244.CrossRefGoogle Scholar
Assi, G.R.S., Franco, G.S. & Vestri, M.S. 2014 b Investigation on the stability of parallel and oblique plates as suppressors of vortex-induced vibration of a circular cylinder. J. Offshore Mech. Arctic Engng 136 (3), 031802.CrossRefGoogle Scholar
Baek, H. & Karniadakis, G. 2012 A convergence study of a new partitioned fluid-structure interaction algorithm based on fictitious mass and damping. J. Comput. Phys. 231, 629–652.CrossRefGoogle Scholar
Bagheri, S., Mazzino, A. & Bottaro, A. 2012 Spontaneous symmetry breaking of a hinged flapping filament generates lift. Phys. Rev. Lett. 109, 154502.CrossRefGoogle ScholarPubMed
Barkley, D., Blackburn, H.M. & Sherwin, S.J. 2008 Direct optimal growth analysis for timesteppers. Intl J. Numer. Meth. Fluids 57 (9), 1435–1458.CrossRefGoogle Scholar
Cantwell, C.D., et al. 2015 Nektar++: an open-source spectral/hp element framework. Comput. Phys. Commun. 192, 205–219.CrossRefGoogle Scholar
Choi, H., Jeon, W.-P. & Kim, J. 2008 Control of flow over a bluff body. Annu. Rev. Fluid Mech. 40 (1), 113–139.CrossRefGoogle Scholar
Chomaz, J.-M. 2005 Global instabilities in spatially developing flows: non-normality and nonlinearity. Annu. Rev. Fluid Mech. 37 (1), 357–392.CrossRefGoogle Scholar
Cimbala, J.M. & Garg, S. 1991 Flow in the wake of a freely rotatable cylinder with splitter plate. AIAA J. 29 (6), 1001–1003.CrossRefGoogle Scholar
Cossu, C. & Morino, L. 2000 On the instability of a spring-mounted circular cylinder in a viscous flow at low Reynolds numbers. J. Fluids Struct. 14, 183–196.CrossRefGoogle Scholar
Dolci, D. & Carmo, B. 2018 Sensitivity analysis applied for a flow around spring-mounted cylinder. In Proceedings of 9th International Symposium on Fluid-Structure Interactions, Flow-Sound Interactions, Flow-Induced Vibration & Noise, Toronto, Ontario, Canada, July 8–11.Google Scholar
Fernandez, M.A. & Tallec, P.L. 2002 Linear stability analysis in fluid-structure interaction with transpiration. Part I: formulation and mathematical analysis. Research Rep. INRIA.Google Scholar
Gerbeau, J.F., Nobile, F. & Causin, P. 2005 Added-mass effect in the design of partitioned algorithms for fluid-structure problems. Comput. Meth. Appl. Mech. Engng 194 (42–44), 4506–4527.Google Scholar
Giannetti, F. & Luchini, P. 2007 Structural sensitivity of the first instability of the cylinder wake. J. Fluid Mech. 581, 167–197.CrossRefGoogle Scholar
Guermond, J.L. & Shen, J. 2003 Velocity-correction projection methods for incompressible flows. SIAM J. Numer. Anal. 41, 112–134.CrossRefGoogle Scholar
Huerre, P. & Monkewitz, P.A. 1990 Local and global instabilities in spatially developing flows. Annu. Rev. Fluid Mech. 22 (1), 473–537.CrossRefGoogle Scholar
Jordi, B.E., Cotter, C.J. & Sherwin, S.J. 2014 Encapsulated formulation of the selective frequency damping method. Phys. Fluids 26, 034101.CrossRefGoogle Scholar
Karniadakis, G.E., Israeli, M. & Orszag, S.A. 1991 High-order splitting methods for the incompressible Navier–Stokes equations. J. Comput. Phys. 97 (2), 414–443.CrossRefGoogle Scholar
Kwon, K. & Choi, H. 1996 Control of laminar vortex shedding behind a circular cylinder using splitter plates. Phys. Fluids 8 (2), 479–486.CrossRefGoogle Scholar
Lacis, U., Brosse, N., Ingremeau, F., Mazzino, A., Lundell, F., Kellay, H. & Bagheri, S. 2014 Passive appendages generate drift through symmetry breaking. Nat. Commun. 5, 5310.CrossRefGoogle ScholarPubMed
Luchini, P. & Bottaro, A. 2014 Adjoint equations in stability analysis. Annu. Rev. Fluid Mech. 46 (1), 493–517.CrossRefGoogle Scholar
Luo, H. & Bewley, T.R. 2004 On the contravariant form of the Navier–Stokes equations in time-dependent curvilinear coordinate system. J. Comput. Phys. 199, 355–375.CrossRefGoogle Scholar
Marquet, O., Sipp, D. & Jacquin, L. 2008 Sensitivity analysis and passive control of cylinder flow. J. Fluid Mech. 615, 221–252.CrossRefGoogle Scholar
Meliga, P. & Chomaz, J.M. 2014 An asymptotic expansion for the vortex-induced vibrations of a circular cylinder. HAL archives-ouvertes HAL-00994505.Google Scholar
Negi, P.S., Hanifi, A. & Henningson, D.S. 2019 Global stability of rigid-body-motion fluid-structure- interaction problems. arXiv:1910.09605.CrossRefGoogle Scholar
Ozono, S. 1999 Flow control of vortex shedding by a short splitter plate asymmetrically arranged downstream of a cylinder. Phys. Fluids 11 (10), 2928–2934.CrossRefGoogle Scholar
Park, H., Bae, K., Lee, B., Jeon, W.P. & Choi, H. 2010 Aerodynamic performance of a gliding swallowtail butterfly wing model. Exp. Mech. 50 (9), 1313–1321.CrossRefGoogle Scholar
Pfister, J.-L. 2019 Instabilities and optimization of elastic structures interacting with laminar flows. PhD thesis, Thèse de doctorat de l'Université Paris-Saclay préparée à l’École polytechnique et à l'Office National d’Études et de Recherches Aérospatiales.Google Scholar
Pfister, J.-L. & Marquet, O. 2020 Fluid structure stability analyses and nonlinear dynamics of flexible splitter plates interacting with a circular cylinder flow. J. Fluid Mech. 896, A24.CrossRefGoogle Scholar
Roshko, A. 1954 On the drag and shedding frequency of two-dimensional bluff bodies. NACA Tech. Note 3169. National Advisory Committee for Aeronautics.Google Scholar
Serson, D., Meneghini, J.R. & Sherwin, S.J. 2016 Velocity-correction schemes for the incompressible Navier–Stokes equations in general coordinate systems. J. Comput. Phys. 316, 243–254.CrossRefGoogle Scholar
Shelley, M.J. & Zhang, J. 2011 Flapping and bending bodies interacting with fluid flows. Annu. Rev. Fluid Mech. 43 (1), 449–465.CrossRefGoogle Scholar
Strykowski, P. & Sreenivasan, K. 1990 On the formation and suppression of vortex at low Reynolds numbers. J. Fluid Mech. 218, 71–107.CrossRefGoogle Scholar
Theofilis, V. 2011 Global linear instability. Annu. Rev. Fluid Mech. 43 (1), 319–352.CrossRefGoogle Scholar
Toebes, G.H. & Eagleson, P.S. 1961 Hydroelastic vibrations of flat plates related to trailing edge geometry. Trans. ASME J. Basic Engng 83, 671–678.CrossRefGoogle Scholar