Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Wei, Nathaniel J.
Kissing, Johannes
and
Tropea, Cameron
2019.
Generation of periodic gusts with a pitching and plunging airfoil.
Experiments in Fluids,
Vol. 60,
Issue. 11,
Neunaber, Ingrid
and
Braud, Caroline
2020.
First characterization of a new perturbation system for gust generation: the chopper.
Wind Energy Science,
Vol. 5,
Issue. 2,
p.
759.
Wu, Zhenlong
Bangga, Galih
Lutz, Thorsten
Kampers, Gerrit
and
Hölling, Michael
2020.
Insights into airfoil response to sinusoidal gusty inflow by oscillating vanes.
Physics of Fluids,
Vol. 32,
Issue. 12,
De Giorgi, Maria Grazia
Motta, Valentina
and
Suma, Antonio
2020.
Influence of actuation parameters of multi-DBD plasma actuators on the static and dynamic behaviour of an airfoil in unsteady flow.
Aerospace Science and Technology,
Vol. 96,
Issue. ,
p.
105587.
He, Xiaowei
and
Williams, David R.
2020.
Spectral feedback control of turbulent spectra in a wind tunnel.
Experiments in Fluids,
Vol. 61,
Issue. 8,
Neunaber, Ingrid
and
Braud, Caroline
2020.
Aerodynamic behavior of an airfoil under extreme wind conditions.
Journal of Physics: Conference Series,
Vol. 1618,
Issue. 3,
p.
032035.
Baddoo, Peter J.
2020.
Lightning Solvers for Potential Flows.
Fluids,
Vol. 5,
Issue. 4,
p.
227.
Jones, Anya R.
2020.
Gust encounters of rigid wings: Taming the parameter space.
Physical Review Fluids,
Vol. 5,
Issue. 11,
Young, Anna M.
and
Smyth, Amanda S.
2020.
The interaction of a Sears-type sinusoidal gust with a cambered aerofoil in the presence of non-uniform streamwise flow.
Mertens, C.
Sciacchitano, A.
van Oudheusden, B.W.
and
Sodja, J.
2021.
An integrated measurement approach for the determination of the aerodynamic loads and structural motion for unsteady airfoils.
Journal of Fluids and Structures,
Vol. 103,
Issue. ,
p.
103293.
Young, Anna M.
and
Smyth, Amanda S. M.
2021.
Gust–Airfoil Coupling with a Loaded Airfoil.
AIAA Journal,
Vol. 59,
Issue. 3,
p.
773.
He, Xiaowei
Asztalos, Katherine J.
Henry, James
Dawson, Scott T.
and
Williams, David R.
2021.
Generating Traveling Cross-Flow Gusts in a Wind Tunnel.
Smyth, Amanda S. M.
Young, Anna M.
and
Di Mare, Luca
2021.
Effect of Three-Dimensional Geometry on Harmonic Gust–Airfoil Interaction.
AIAA Journal,
Vol. 59,
Issue. 2,
p.
737.
Fernandez, Fidel
Cleaver, David
and
Gursul, Ismet
2021.
Unsteady aerodynamics of a wing in a novel small-amplitude transverse gust generator.
Experiments in Fluids,
Vol. 62,
Issue. 1,
Baddoo, Peter J.
Hajian, Rozhin
and
Jaworski, Justin W.
2021.
Unsteady aerodynamics of porous aerofoils.
Journal of Fluid Mechanics,
Vol. 913,
Issue. ,
Grifith, Tristan D.
Gehlot, Vinod P.
and
Balas, Mark J.
2022.
Adaptive Estimation of Unknown Inputs with Weakly Nonlinear Dynamics.
p.
5043.
Sun, Shu
Wu, Zhenlong
Huang, Hexia
Bangga, Galih
and
Tan, Huijun
2022.
Aerodynamic Response of a Serpentine Inlet to Horizontal Periodic Gusts.
Aerospace,
Vol. 9,
Issue. 12,
p.
824.
Wester, Tom T. B.
Krauss, Johannes
Neuhaus, Lars
Hölling, Agnieszka
Gülker, Gerd
Hölling, Michael
and
Peinke, Joachim
2022.
How to Design a 2D Active Grid for Dynamic Inflow Modulation.
Flow, Turbulence and Combustion,
Vol. 108,
Issue. 4,
p.
955.
Wang, Tong
and
Feng, Li-Hao
2022.
Characterization of vertical and longitudinal gusts generated by twin pitching airfoils.
Physics of Fluids,
Vol. 34,
Issue. 9,
Soto-Valle, R.
Gualtieri, M.
Bartholomay, S.
Manolesos, M.
Nayeri, C.N.
Bianchini, A.
and
Paschereit, C.O.
2022.
Rotational and blockage effects on a wind turbine model based on local blade forces.
Journal of Physics: Conference Series,
Vol. 2265,
Issue. 2,
p.
022102.
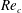 $Re_{c}$) of
$Re_{c}$) of 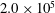 $2.0\times 10^{5}$ and
$2.0\times 10^{5}$ and 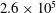 $2.6\times 10^{5}$ and reduced frequencies between
$2.6\times 10^{5}$ and reduced frequencies between 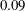 $0.09$ and
$0.09$ and 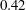 $0.42$ confirm that the Sears and Atassi functions differ only in convention: the additional gust component of the Atassi problem can be scaled so that the Atassi function collapses onto the Sears function. These experiments, complemented by numerical simulations of the set-up, validate both models across a range of gust parameters. Finally, the influence of boundary-layer turbulence and the turbulent wake of the gust generator on experimental convergence with model predictions is investigated. These results serve to clarify the conditions under which the Sears and Atassi functions can be applied, and demonstrate that the Sears function can effectively model unsteady forces even when significant fluctuations in the streamwise velocity are present.
$0.42$ confirm that the Sears and Atassi functions differ only in convention: the additional gust component of the Atassi problem can be scaled so that the Atassi function collapses onto the Sears function. These experiments, complemented by numerical simulations of the set-up, validate both models across a range of gust parameters. Finally, the influence of boundary-layer turbulence and the turbulent wake of the gust generator on experimental convergence with model predictions is investigated. These results serve to clarify the conditions under which the Sears and Atassi functions can be applied, and demonstrate that the Sears function can effectively model unsteady forces even when significant fluctuations in the streamwise velocity are present.