Hostname: page-component-78c5997874-dh8gc Total loading time: 0 Render date: 2024-11-16T15:06:26.687Z Has data issue: false hasContentIssue false
  • English
  • Français

Influence of the inlet velocity profile on the flow stability in a symmetric channel expansion

Published online by Cambridge University Press:  22 December 2020

Robin Debuysschère Open the ORCID record for Robin Debuysschère [Opens in a new window] ,
Lorenzo Siconolfi ,
Bart Rimez ,
François Gallaire Open the ORCID record for François Gallaire [Opens in a new window]  and
Benoit Scheid Open the ORCID record for Benoit Scheid [Opens in a new window]
Robin Debuysschère
Affiliation:
Transfers, Interfaces and Processes (TIPs), ULB, 1050Brussels, Belgium
Lorenzo Siconolfi
Affiliation:
Laboratory of Fluid Mechanics and Instabilities (LFMI), EPFL, 1015Lausanne, Switzerland
Bart Rimez
Affiliation:
Transfers, Interfaces and Processes (TIPs), ULB, 1050Brussels, Belgium
François Gallaire
Affiliation:
Laboratory of Fluid Mechanics and Instabilities (LFMI), EPFL, 1015Lausanne, Switzerland
Benoit Scheid*
Affiliation:
Transfers, Interfaces and Processes (TIPs), ULB, 1050Brussels, Belgium
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

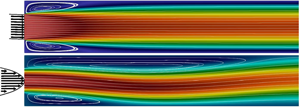
In a channel flow with a sudden expansion, whether for three-dimensional (3-D) pipe and channel flows, or for two-dimensional (2-D) channel flow, it is known that increasing the Reynolds number beyond a critical value $Re_c$ induces a symmetry breaking Pitchfork bifurcation. The linear stability analysis of the symmetric steady solution enables the $Re_c$ to be determined efficiently and thus the influence of the expansion ratio ($ER$), defined as the ratio between upstream and downstream diameter regarding the expansion, to be explored. In this study, we investigate the behaviour of the flow after 2-D sudden expansions while varying the $ER$ and the inlet flow profile, e.g. corresponding to a transition profile between a plug and a Poiseuille flow that could be reached for a flow after a sudden constriction upstream. Results demonstrate that imposing a plug flow at the inlet gives a higher $Re_c$ than any other profile and that the concomitant recirculation zones are shorter. We show that these results can be rationalized using basic convection–diffusion arguments.

JFM classification

Mathematical Foundations: Computational methods Nonlinear Dynamical Systems: Bifurcation Instability: Transition to turbulence
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 909 , 25 February 2021 , A13
Check for updates
Copyright
© The Author(s), 2020. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Back, L. H. & Roschke, E. J. 1972 Shear-layer flow regimes and wave instabilities and reattachment lengths downstream of an abrupt circular channel expansion. Trans. ASME: J. Appl. Mech. 39 (3), 677–681.CrossRefGoogle Scholar
Battaglia, F. & Papadopoulos, G. 2005 Bifurcation characteristics of flows in rectangular sudden expansion channels. In Volume 1: Symposia, Parts A and B, vol. 2005, pp. 91–101. ASME.CrossRefGoogle Scholar
Battaglia, F., Tavener, S. J., Kulkarni, A. K. & Merkle, Ch. L. 1997 Bifurcation of low Reynolds number flows in symmetric channels. AIAA J. 35 (1), 99–105.CrossRefGoogle Scholar
Cantwell, C. D., Barkley, D. & Blackburn, H. M. 2010 Transient growth analysis of flow through a sudden expansion in a circular pipe. Phys. Fluids 22 (3), 034101.CrossRefGoogle Scholar
Chang, H., Huang, C., Li, P. & Jen, C. 2010 Design of a blood-plasma separation microfluidic chip utilizing backward facing step geometry. In IEEE 5th International Conference on Nano/Micro Engineered and Molecular Systems, pp. 912–914.Google Scholar
Dagtekin, I. & Unsal, M. 2011 Numerical analysis of axisymmetric and planar sudden expansion flows for laminar regime. Intl J. Numer. Meth. Fluids 65 (9), 1133–1144.CrossRefGoogle Scholar
Drikakis, D. 1997 Bifurcation phenomena in incompressible sudden expansion flows. Phys. Fluids 9 (1), 76–87.CrossRefGoogle Scholar
Durst, F. & Loy, T. 1985 Investigations of laminar flow in a pipe with sudden contraction of cross sectional area. Comput. Fluids 13 (1), 15–36.CrossRefGoogle Scholar
Fani, A., Camarri, S. & Salvetti, M. V. 2012 Stability analysis and control of the flow in a symmetric channel with a sudden expansion. Phys. Fluids 24 (8), 084102.CrossRefGoogle Scholar
Fischer, P. F., Lottes, J. W. & Kerkemeier, S. G. 2008 NEK5000 documentation. Available at: http://nek5000.mcs.anl.gov.Google Scholar
Hallett, W. L. H. & Gunther, R. 1984 Flow and mixing in swirling flow in a sudden expansion. Can. J. Chem. Engng 62 (1), 149–155.CrossRefGoogle Scholar
Hecht, F. 2012 New development in freefem++. J. Numer. Maths 20 (3–4), 251–266.Google Scholar
Kadivar, E. & Farrokhbin, M. 2017 A numerical procedure for scaling droplet deformation in a microfluidic expansion channel. Physica A 479, 449–459.CrossRefGoogle Scholar
Khodaparast, S., Borhani, N. & Thome, J. R. 2014 Sudden expansions in circular microchannels: flow dynamics and pressure drop. Microfluid Nanofluid 17 (3), 561–572.CrossRefGoogle Scholar
Latornell, D. J. & Pollard, A. 1986 Some observations on the evolution of shear layer instabilities in laminar flow through axisymmetric sudden expansions. Phys. Fluids 29 (9), 2828–2835.CrossRefGoogle Scholar
Lautrup, B. 2011 Physics of Continuous Matter: Exotic and Everyday Phenomena in the Macroscopic World, 2nd edn. Taylor & Francis.CrossRefGoogle Scholar
Mishra, S. & Jayaraman, K. 2002 Asymmetric flows in planar symmetric channels with large expansion ratio. Intl J. Numer. Meth. Fluids 38 (10), 945–962.CrossRefGoogle Scholar
Morini, G. L. 2004 Laminar-to-turbulent flow transition in microchannels. Microscale Therm. Engng 8, 15–30.CrossRefGoogle Scholar
Mullin, T., Seddon, J. R. T., Mantle, M. D. & Sederman, A. J. 2009 Bifurcation phenomena in the flow through a sudden expansion in a circular pipe. Phys. Fluids 21 (1), 014110.CrossRefGoogle Scholar
Park, J.-S., Song, S.-H. & Jung, H.-I. 2009 Continuous focusing of microparticles using inertial lift force and vorticity via multi-orifice microfluidic channels. Lab on a Chip 9 (7), 939–948.CrossRefGoogle ScholarPubMed
Potter, M. C. 1971 Linear stability of turbulent flow profiles. Phys. Fluids 14 (7), 1323.CrossRefGoogle Scholar
Qian, J., Ma, L., Zhan, H., Luo, Q., Wang, X. & Wang, M. 2016 The effect of expansion ratio on the critical Reynolds number in single fracture flow with sudden expansion: the effect of expansion ratio on the critical Reynolds number. Hydrol. Process. 30 (11), 1718–1726.CrossRefGoogle Scholar
Rimez, B., Debuysschère, R., Conté, J., Lecomte-Norrant, E., Gourdon, C., Cognet, P. & Scheid, B. 2018 Continuous-flow tubular crystallization to discriminate between two competing crystal polymorphs. 1. Cooling crystallization. Cryst. Growth Des. 18 (11), 6431–6439.CrossRefGoogle Scholar
Rimez, B., Debuysschère, R. & Scheid, B. 2019 On the effect of flow restrictions on the nucleation behavior of molecules in tubular flow nucleators. J. Flow Chem. 10, 241–249.CrossRefGoogle Scholar
Sanmiguel-Rojas, E. & Mullin, T. 2012 Finite-amplitude solutions in the flow through a sudden expansion in a circular pipe. J. Fluid Mech. 691, 201–213.CrossRefGoogle Scholar
Ternik, P. 2009 Planar sudden symmetric expansion flows and bifurcation phenomena of purely viscous shear-thinning fluids. J. Non-Newtonian Fluid Mech. 157 (1–2), 15–25.CrossRefGoogle Scholar
Tsai, C.-H., Chen, H.-T., Wang, Y.-N., Lin, C.-H. & Fu, L.-M. 2006 Capabilities and limitations of 2-dimensional and 3-dimensional numerical methods in modeling the fluid flow in sudden expansion microchannels. Microfluid Nanofluid 3 (1), 13–18.CrossRefGoogle Scholar
Vaniershot, M. & Van den Bulck, E. 2008 The influence of swirl on the reattachment length in an abrupt axisymmetric expansion. Intl J. Heat Fluid Flow 29, 75–82.CrossRefGoogle Scholar
Volpe, A., Gaudiuso, C. & Ancona, A. 2019 Sorting of particles using inertial focusing and laminar vortex technology: a review. Micromachines 10, 594.CrossRefGoogle ScholarPubMed
Wang, Ch., Gao, P.-Z., Tan, S.-Ch. & Xu, Ch. 2012 Effect of aspect ratio on the laminar-to-turbulent transition in rectangular channel. Ann. Nucl. Energy 46, 90–96.Google Scholar
Zhang, J. & Luo, X. 2018 Mixing performance of a 3D micro t-mixer with swirling-inducing inlets and rectangular constriction. Micromachines 9 (5), 199.CrossRefGoogle ScholarPubMed
Zohir, A. E., Abdel Aziz, A. A. & Habib, M. A. 2011 Heat transfer characteristics in a sudden expansion pipe equipped with swirl generators. Intl J. Heat Fluid Flow 32 (1), 352–361.CrossRefGoogle Scholar