1. Introduction
Wave breaking poses an upper limit to how steep an individual wave can become, is the main mechanism of dissipation of wave energy in the ocean, and determines how sea states evolve (Hasselmann Reference Hasselmann1974; Phillips Reference Phillips1985; Young & Babanin Reference Young and Babanin2006; Iafrati Reference Iafrati2011; Romero, Melville & Kleiss Reference Romero, Melville and Kleiss2012; Sutherland & Melville Reference Sutherland and Melville2013). Wave breaking also affects turbulence and mixing in the upper ocean and contributes significantly to air–sea interaction (Melville Reference Melville1996; Deike Reference Deike2022). The interaction of the atmosphere and the ocean plays a leading role in the uptake of anthropogenic ![]() ${\rm CO}_2$ by the ocean, and is thus of crucial importance to understanding climate change (Smith & Jones Reference Smith and Jones1985; Reichl & Deike Reference Reichl and Deike2020). Understanding how and when waves break is, therefore, essential for forecasting (extreme) waves, predicting the resulting loads they exert on offshore structures and climate modelling.
${\rm CO}_2$ by the ocean, and is thus of crucial importance to understanding climate change (Smith & Jones Reference Smith and Jones1985; Reichl & Deike Reference Reichl and Deike2020). Understanding how and when waves break is, therefore, essential for forecasting (extreme) waves, predicting the resulting loads they exert on offshore structures and climate modelling.
Stokes (Reference Stokes1880) first proposed a limiting form for two-dimensional (2-D) progressive waves on deep water, where the steepest possible wave crest encloses an angle of ![]() $120\,^\circ$. This waveform corresponds to a steepness of
$120\,^\circ$. This waveform corresponds to a steepness of ![]() $kH/2=0.44$, where
$kH/2=0.44$, where ![]() $H$ is wave height and
$H$ is wave height and ![]() $k$ is wavenumber (see figure 1). However, waves in the ocean are not of permanent progressive form, and field and laboratory observations of waves steeper than this limit are not uncommon (Toffoli et al. Reference Toffoli, Babanin, Onorato and Waseda2010); observations of breaking below this threshold are also frequently made (Perlin, Choi & Tian Reference Perlin, Choi and Tian2013). Various external factors may cause deviations from this theoretical limit; for example, the interaction of winds and currents with waves can strongly modulate the onset of breaking (Wu & Yao Reference Wu and Yao2004; Babanin et al. Reference Babanin, Chalikov, Young and Savelyev2010; VreĆica, Pizzo & Lenain Reference VreĆica, Pizzo and Lenain2022). In the absence of external factors, the mechanism by which large wave crests are formed is also thought to influence breaking onset; waves that form as a result of (linear) dispersive focusing and those that form as a result of (nonlinear) modulational instability have been shown to break at different steepness (Perlin et al. Reference Perlin, Choi and Tian2013).
$k$ is wavenumber (see figure 1). However, waves in the ocean are not of permanent progressive form, and field and laboratory observations of waves steeper than this limit are not uncommon (Toffoli et al. Reference Toffoli, Babanin, Onorato and Waseda2010); observations of breaking below this threshold are also frequently made (Perlin, Choi & Tian Reference Perlin, Choi and Tian2013). Various external factors may cause deviations from this theoretical limit; for example, the interaction of winds and currents with waves can strongly modulate the onset of breaking (Wu & Yao Reference Wu and Yao2004; Babanin et al. Reference Babanin, Chalikov, Young and Savelyev2010; VreĆica, Pizzo & Lenain Reference VreĆica, Pizzo and Lenain2022). In the absence of external factors, the mechanism by which large wave crests are formed is also thought to influence breaking onset; waves that form as a result of (linear) dispersive focusing and those that form as a result of (nonlinear) modulational instability have been shown to break at different steepness (Perlin et al. Reference Perlin, Choi and Tian2013).

Figure 1. Definition of zero-crossing wave height ![]() $H$, wavelength
$H$, wavelength ![]() $\lambda$ (
$\lambda$ (![]() $k=2{\rm \pi} /\lambda$), crest length
$k=2{\rm \pi} /\lambda$), crest length ![]() $\lambda _c$ and (crest) amplitude
$\lambda _c$ and (crest) amplitude ![]() $a$ relative to the still-water level (SWL).
$a$ relative to the still-water level (SWL).
Broadly speaking, the different mechanisms (dispersion and nonlinearity) that generate extreme (steep) waves crest are strongly influenced by the bandwidth of the underlying spectrum. In two dimensions, bandwidth corresponds to the range of frequencies over which wave energy is present; in three dimensions, bandwidth also corresponds to the degree of directional spreading of a given sea state. In moderately spread unimodal conditions, directional spreading (directional bandwidth) has been shown to increase the steepness at which breaking onset occurs (Johannessen & Swan Reference Johannessen and Swan2001; Latheef & Swan Reference Latheef and Swan2013). For crossing-sea conditions, where the directional spectrum is bimodal, breaking onset steepness increases with the angle of crossing (McAllister et al. Reference McAllister, Draycott, Adcock, Taylor and van den Bremer2019). In general, increasing directional bandwidth appears to increase the steepness at which wave breaking onset occurs. It is worth noting that numerical studies involving ‘short-crested’ waves created by varying the angle between two monochromatic waves demonstrate a non-monotonic increase in breaking onset steepness as the angle is increased (Roberts & Schwartz Reference Roberts and Schwartz1983; Tsai, Jeng & Hsu Reference Tsai, Jeng and Hsu1994). Owing to the challenges associated with modelling highly directionally spread waves experimentally and numerically, the relationship between spreading and breaking onset is not fully understood.
In two dimensions, frequency bandwidth affects the duration over which waves may interact nonlinearly, meaning that modulational instability dominates when the underlying spectrum is narrow and waves have sufficient time to interact. Paired with a measure of steepness, bandwidth may be used to characterise the impact of nonlinearity vs dispersion in the steepening and potential overturning of surface waves (Pizzo, Melville & Deike Reference Pizzo, Melville and Deike2019). However, there may not be a unique way to do this (Perlin et al. Reference Perlin, Choi and Tian2013), and existing studies carried out in two dimensions appear not to reach clear consensus regarding frequency bandwidth's effect on breaking onset (see table 1 and figure 2 for an overview of these studies). One example of this lack of consensus can be found when comparing Wu & Yao (Reference Wu and Yao2004) and Pizzo et al. (Reference Pizzo, Murray, Smith and Lenain2021), who examined wave groups based on constant-steepness spectra created experimentally and numerically, respectively. Wu & Yao (Reference Wu and Yao2004) observed a decreasing relationship,
(note in their (9) Wu & Yao (Reference Wu and Yao2004) use ![]() $a$ to denote
$a$ to denote ![]() $H/2$ in contrast to our notation defined in figure 1), whereas Pizzo et al. (Reference Pizzo, Murray, Smith and Lenain2021) observe an increasing relationship,
$H/2$ in contrast to our notation defined in figure 1), whereas Pizzo et al. (Reference Pizzo, Murray, Smith and Lenain2021) observe an increasing relationship,
between the breaking onset steepness measures (![]() $kH/2$,
$kH/2$, ![]() $S$) and the bandwidth measures (
$S$) and the bandwidth measures (![]() $\nu$,
$\nu$, ![]() $\varDelta$) these authors consider. A number of factors, such as inconsistent definitions of steepness, may explain this apparent contradiction. Furthermore, it is important to note that different studies have used a range of different spectral shapes to create breaking wave groups, such as constant-amplitude spectra (Rapp & Melville Reference Rapp and Melville1990; Wu & Yao Reference Wu and Yao2004), constant-steepness spectra (Wu & Yao Reference Wu and Yao2004; Pizzo et al. Reference Pizzo, Murray, Smith and Lenain2021), JONSWAP spectra (Craciunescu & Christou Reference Craciunescu and Christou2020) and chirped wave packets (Song & Banner Reference Song and Banner2002; Saket et al. Reference Saket, Peirson, Banner, Barthelemy and Allis2017; Barthelemy et al. Reference Barthelemy, Banner, Peirson, Fedele, Allis and Dias2018; Pizzo & Melville Reference Pizzo and Melville2019).
$\varDelta$) these authors consider. A number of factors, such as inconsistent definitions of steepness, may explain this apparent contradiction. Furthermore, it is important to note that different studies have used a range of different spectral shapes to create breaking wave groups, such as constant-amplitude spectra (Rapp & Melville Reference Rapp and Melville1990; Wu & Yao Reference Wu and Yao2004), constant-steepness spectra (Wu & Yao Reference Wu and Yao2004; Pizzo et al. Reference Pizzo, Murray, Smith and Lenain2021), JONSWAP spectra (Craciunescu & Christou Reference Craciunescu and Christou2020) and chirped wave packets (Song & Banner Reference Song and Banner2002; Saket et al. Reference Saket, Peirson, Banner, Barthelemy and Allis2017; Barthelemy et al. Reference Barthelemy, Banner, Peirson, Fedele, Allis and Dias2018; Pizzo & Melville Reference Pizzo and Melville2019).
Table 1. Summary of comparable 2-D laboratory (L) and numerical (N) studies of breaking onset on deep and intermediate water. Some of the values not presented explicitly in the cited references have been extracted from digitised figures, and several are taken from Perlin et al. (Reference Perlin, Choi and Tian2013). Initial monochromatic steepness (IMS) is used to characterise the steepness of modulated wave trains (MWTs). For focused wave groups we present ![]() $S$ where available; values that correspond to local measures of steepness
$S$ where available; values that correspond to local measures of steepness ![]() $kH/2$,
$kH/2$, ![]() $ak$ and
$ak$ and ![]() $a{\rm \pi} /\lambda _c$ are labelled with
$a{\rm \pi} /\lambda _c$ are labelled with ![]() $*$,
$*$, ![]() ${\dagger}$ and
${\dagger}$ and ![]() $\ddagger$ symbols, respectively. Experiments in which values of
$\ddagger$ symbols, respectively. Experiments in which values of ![]() $S$ based on measurements were reported (i.e.
$S$ based on measurements were reported (i.e. ![]() $S=\sum a_nk_n \cos (\theta _n)$) we denote with a
$S=\sum a_nk_n \cos (\theta _n)$) we denote with a ![]() $\star$ symbol. Values of bandwidth
$\star$ symbol. Values of bandwidth ![]() $\nu$ that we have calculated based on the reported spectral shape are labelled with a letter
$\nu$ that we have calculated based on the reported spectral shape are labelled with a letter ![]() $c$. For the chirped wave packets in Pizzo & Melville (Reference Pizzo and Melville2019), we report the 3-dB limits as a measure of bandwidth.
$c$. For the chirped wave packets in Pizzo & Melville (Reference Pizzo and Melville2019), we report the 3-dB limits as a measure of bandwidth.


Figure 2. Breaking threshold steepness as a function of bandwidth taken from existing experimental and numerical studies. Filled markers show global (i.e. ![]() $S$) and open markers show local measures of steepness (i.e.
$S$) and open markers show local measures of steepness (i.e. ![]() $ak$,
$ak$, ![]() $kH/2$, or
$kH/2$, or ![]() $a{\rm \pi} /\lambda _c$); circular markers correspond to wave groups based on constant-steepness spectra, stars to linear steepness spectra, triangles to constant-amplitude spectra, diamonds to JONSWAP spectra and squares to chirped wave packets (see table 1). Colours denote the different studies as given in the legend. Dashed lines show the parametric breaking thresholds (1.2) and (1.1).
$a{\rm \pi} /\lambda _c$); circular markers correspond to wave groups based on constant-steepness spectra, stars to linear steepness spectra, triangles to constant-amplitude spectra, diamonds to JONSWAP spectra and squares to chirped wave packets (see table 1). Colours denote the different studies as given in the legend. Dashed lines show the parametric breaking thresholds (1.2) and (1.1).
When different spectral shapes are used, the definition of spectral bandwidth itself may become a source of inconsistency. For constant-amplitude and constant-steepness spectra, it is intuitive to define bandwidth as the range of frequencies over which the spectrum is defined ![]() $\Delta f$, and when using a JONSWAP spectrum the peak enhancement factor
$\Delta f$, and when using a JONSWAP spectrum the peak enhancement factor ![]() $\gamma$ may be used to define bandwidth. The parameter
$\gamma$ may be used to define bandwidth. The parameter ![]() $\nu$, which is calculated as
$\nu$, which is calculated as ![]() $\sqrt {m_0m_2/m_1^2-1}$ with
$\sqrt {m_0m_2/m_1^2-1}$ with ![]() $m_n$ the
$m_n$ the ![]() $n{\rm th}$ spectral moment of the energy spectrum
$n{\rm th}$ spectral moment of the energy spectrum ![]() $E(f)$, may be used to provide a more general definition of bandwidth. When
$E(f)$, may be used to provide a more general definition of bandwidth. When ![]() $\nu$ is used as a measure of bandwidth, the results of Craciunescu & Christou (Reference Craciunescu and Christou2020) (JONSWAP spectrum) show an opposite relationship of breaking onset steepness with bandwidth compared with Pizzo et al. (Reference Pizzo, Murray, Smith and Lenain2021) (constant-steepness spectrum) when the same measure of steepness is used as a breaking onset threshold, with the former (Craciunescu & Christou Reference Craciunescu and Christou2020) decreasing in figure 2(b) and the latter (Pizzo et al. Reference Pizzo, Murray, Smith and Lenain2021) increasing in figure 2(a) (we note that the variation in breaking onset steepness observed in Craciunescu & Christou (Reference Craciunescu and Christou2020) is very small, see figure 2b). This may suggest that, even if bandwidth is defined consistently, spectral shape has an influence on the relationship between bandwidth and breaking onset.
$\nu$ is used as a measure of bandwidth, the results of Craciunescu & Christou (Reference Craciunescu and Christou2020) (JONSWAP spectrum) show an opposite relationship of breaking onset steepness with bandwidth compared with Pizzo et al. (Reference Pizzo, Murray, Smith and Lenain2021) (constant-steepness spectrum) when the same measure of steepness is used as a breaking onset threshold, with the former (Craciunescu & Christou Reference Craciunescu and Christou2020) decreasing in figure 2(b) and the latter (Pizzo et al. Reference Pizzo, Murray, Smith and Lenain2021) increasing in figure 2(a) (we note that the variation in breaking onset steepness observed in Craciunescu & Christou (Reference Craciunescu and Christou2020) is very small, see figure 2b). This may suggest that, even if bandwidth is defined consistently, spectral shape has an influence on the relationship between bandwidth and breaking onset.
Table 1 lists the breaking onset steepness threshold values found in comparable studies of 2-D wave breaking onset (on deep and intermediate water depths). Figure 2 plots breaking onset steepness reported in the studies listed in table 1 as a function of the bandwidth measures ![]() $\varDelta =\Delta f/f_0$ when applicable (left), where
$\varDelta =\Delta f/f_0$ when applicable (left), where ![]() $f_0$ is the central frequency, and
$f_0$ is the central frequency, and ![]() $\nu$ (right). We exclude studies that examine breaking onset of modulated wave trains from this figure, and note that modulated wave trains, given sufficient distance to propagate, can break with initial monochromatic steepness as low as
$\nu$ (right). We exclude studies that examine breaking onset of modulated wave trains from this figure, and note that modulated wave trains, given sufficient distance to propagate, can break with initial monochromatic steepness as low as ![]() $0.08$ (Dold & Peregrine Reference Dold and Peregrine1986b; Babanin et al. Reference Babanin, Chalikov, Young and Savelyev2010). Open markers denote local measures of steepness (e.g.
$0.08$ (Dold & Peregrine Reference Dold and Peregrine1986b; Babanin et al. Reference Babanin, Chalikov, Young and Savelyev2010). Open markers denote local measures of steepness (e.g. ![]() $kH/2$,
$kH/2$, ![]() $ak$), and filled markers denote global steepness (
$ak$), and filled markers denote global steepness (![]() $S=\sum a_n k_n \equiv k_c \sum a_n\equiv a_0 k_c$, where
$S=\sum a_n k_n \equiv k_c \sum a_n\equiv a_0 k_c$, where ![]() $k_c$ is the characteristic wavenumber).
$k_c$ is the characteristic wavenumber).
The results of Wu & Yao (Reference Wu and Yao2004) show a significant inverse relationship between bandwidth and breaking onset steepness and were used to fit (1.1) (Wu & Yao Reference Wu and Yao2004); their values of breaking onset steepness are measured locally. Local steepness is also reported in Johannessen & Swan (Reference Johannessen and Swan2001), Saket et al. (Reference Saket, Peirson, Banner, Barthelemy and Allis2017) and Barthelemy et al. (Reference Barthelemy, Banner, Peirson, Fedele, Allis and Dias2018); all three studies report significantly higher breaking onset steepness than Wu & Yao (Reference Wu and Yao2004). We note that Saket et al. (Reference Saket, Peirson, Banner, Barthelemy and Allis2017) and Barthelemy et al. (Reference Barthelemy, Banner, Peirson, Fedele, Allis and Dias2018) report local crest steepness ![]() $a{\rm \pi} /\lambda _c$, where
$a{\rm \pi} /\lambda _c$, where ![]() $\lambda _c$ is the crest length (see figure 1). The values reported in Johannessen & Swan (Reference Johannessen and Swan2001) decrease as a function of bandwidth, in a similar manner to (1.1) albeit with higher values of breaking onset steepness. In Saket et al. (Reference Saket, Peirson, Banner, Barthelemy and Allis2017) and Barthelemy et al. (Reference Barthelemy, Banner, Peirson, Fedele, Allis and Dias2018) bandwidth did not vary sufficiently to observe a trend. Johannessen & Swan (Reference Johannessen and Swan2001) also reported values of global breaking onset steepness for their experiments (solid markers of the same colour), which did not vary significantly with bandwidth; this is also the case for values of global steepness reported by Rapp & Melville (Reference Rapp and Melville1990). The numerical numerical results presented in Song & Banner (Reference Song and Banner2002) show global breaking onset steepness increasing with bandwidth over the small range of bandwidths that they performed simulations for. The experimental results reported in Sinnis et al. (Reference Sinnis, Grare, Lenain and Pizzo2021) show good agreement with the parameterisation (1.2) (emphasising the latter is obtained from numerical simulations). In Sinnis et al. (Reference Sinnis, Grare, Lenain and Pizzo2021), the linear predictions of maximum surface slope (global steepness) were calculated using phases and amplitudes measured close to the point of wave generation, which means these results do not rely on perfect wave generation and are most likely more accurate.
$\lambda _c$ is the crest length (see figure 1). The values reported in Johannessen & Swan (Reference Johannessen and Swan2001) decrease as a function of bandwidth, in a similar manner to (1.1) albeit with higher values of breaking onset steepness. In Saket et al. (Reference Saket, Peirson, Banner, Barthelemy and Allis2017) and Barthelemy et al. (Reference Barthelemy, Banner, Peirson, Fedele, Allis and Dias2018) bandwidth did not vary sufficiently to observe a trend. Johannessen & Swan (Reference Johannessen and Swan2001) also reported values of global breaking onset steepness for their experiments (solid markers of the same colour), which did not vary significantly with bandwidth; this is also the case for values of global steepness reported by Rapp & Melville (Reference Rapp and Melville1990). The numerical numerical results presented in Song & Banner (Reference Song and Banner2002) show global breaking onset steepness increasing with bandwidth over the small range of bandwidths that they performed simulations for. The experimental results reported in Sinnis et al. (Reference Sinnis, Grare, Lenain and Pizzo2021) show good agreement with the parameterisation (1.2) (emphasising the latter is obtained from numerical simulations). In Sinnis et al. (Reference Sinnis, Grare, Lenain and Pizzo2021), the linear predictions of maximum surface slope (global steepness) were calculated using phases and amplitudes measured close to the point of wave generation, which means these results do not rely on perfect wave generation and are most likely more accurate.
The data as a whole do not show a clear and consistent relationship between breaking onset steepness and either measure of bandwidth. The majority of the data in figure 2 are based on experiments in which constant-steepness spectra were used, so, while some of the scatter may be a result of the different spectral shapes studied, the scatter may not be explained by differences in spectral shape alone. What is made clear in figure 2, and in Rapp & Melville (Reference Rapp and Melville1990) and Johannessen & Swan (Reference Johannessen and Swan2001), is that using global and local definitions of steepness may lead to conflicting outcomes; we investigate this in detail in §§ 3 and 4.
Generating breaking waves experimentally is challenging, doing so over a wide range of bandwidths is even more so, as experiments involving narrow bandwidths require very long flumes. In addition, measuring the relevant spatial characteristics and kinematics of breaking waves experimentally is also difficult. Numerical simulations offer the ability to examine wave properties readily with high spatial resolution, although it is evidently more difficult to include in numerical simulations the non-potential-flow effects that start to occur after breaking onset.
In this paper, we perform a series of 2-D fully nonlinear Lagrangian potential-flow simulations based on the numerical method proposed in Dold & Peregrine (Reference Dold and Peregrine1986a), with the aim of elucidating the effects bandwidth and spectral shape have on wave breaking onset, and to reconcile existing studies, which appear to disagree. We analyse focused wave groups, varying spectral shape and bandwidth, and investigate how the onset of wave breaking is affected. We detail how we define focused wave groups in § 2, we then examine properties of steep and breaking focused wave groups subject to linear (§ 3) and fully nonlinear evolution (§ 4). Finally, we discuss our results and draw conclusions in § 5.
2. Definitions of focused wave groups
In the following sections (§§ 3 and 4), we examine the properties of focused wave groups relevant to wave breaking, first examining results based on linear wave theory in § 3 and then based on fully nonlinear numerical simulations in § 4. In both cases, initial conditions are obtained using linear wave theory in the same manner, which we define in this section.
2.1. Linear initial conditions
We define linear surface elevation
 \begin{equation} \eta^{(1)}(x,t)=\sum_{n=1}^{N}a_{n}\cos(\theta_n),\quad \mathrm{where}\ \theta_n=k_n x-\omega_n t+\varphi_n, \end{equation}
\begin{equation} \eta^{(1)}(x,t)=\sum_{n=1}^{N}a_{n}\cos(\theta_n),\quad \mathrm{where}\ \theta_n=k_n x-\omega_n t+\varphi_n, \end{equation}and velocity potential
 \begin{equation} \phi^{(1)}(x,z,t)=\sum_{n=1}^{N}a_{n}\frac{\omega_n}{k_n}\exp\left(k_n z\right)\sin(\theta_n), \end{equation}
\begin{equation} \phi^{(1)}(x,z,t)=\sum_{n=1}^{N}a_{n}\frac{\omega_n}{k_n}\exp\left(k_n z\right)\sin(\theta_n), \end{equation}
as a summation of ![]() $N$ free wave components propagating on deep water, with amplitude
$N$ free wave components propagating on deep water, with amplitude ![]() $a_n$, frequency
$a_n$, frequency ![]() $\omega _n$ and wavenumber
$\omega _n$ and wavenumber ![]() $k_n$, obeying the linear dispersion relationship
$k_n$, obeying the linear dispersion relationship ![]() $\omega _n^2=gk_n$ with
$\omega _n^2=gk_n$ with ![]() $g$ the gravitational acceleration. Waves propagate in the positive
$g$ the gravitational acceleration. Waves propagate in the positive ![]() $x$ direction,
$x$ direction, ![]() $z$ is positive in the upwards direction, with
$z$ is positive in the upwards direction, with ![]() $z=0$ corresponding to the still-water level and
$z=0$ corresponding to the still-water level and ![]() $t$ is time. The phases
$t$ is time. The phases ![]() $\varphi _n$ are defined such that all components are in phase at the desired focus time (
$\varphi _n$ are defined such that all components are in phase at the desired focus time (![]() $t=0$) and position (
$t=0$) and position (![]() $x=0$). Defining phases in this manner creates a focused wave group, assuming linear dispersive focusing.
$x=0$). Defining phases in this manner creates a focused wave group, assuming linear dispersive focusing.
2.2. Frequency spectra
In the existing literature, various different spectra have been used to generate breaking wave groups (see table 1). To understand why differences in breaking behaviour observed in previous studies may arise, we examine three spectral shapes, namely constant-steepness and constant-amplitude spectra (§ 2.2.1) and JONSWAP spectra (§ 2.2.2). In each case, we define the amplitude spectrum, ![]() $\hat {\eta }^{(1)}(f)=\int \eta ^{(1)}(t)\exp ({\rm i}2{\rm \pi} ft)\,{\rm d}t$, from which initial conditions (2.1)–(2.2) are obtained using properties of linear dispersion.
$\hat {\eta }^{(1)}(f)=\int \eta ^{(1)}(t)\exp ({\rm i}2{\rm \pi} ft)\,{\rm d}t$, from which initial conditions (2.1)–(2.2) are obtained using properties of linear dispersion.
2.2.1. Constant-amplitude and constant-steepness spectra
Perhaps the most simple and the most commonly used (cf. table 1) spectra are those for which the spectral components have constant amplitude or steepness, for which the amplitude spectra have the general form
where ![]() $f_0$ is the central frequency and
$f_0$ is the central frequency and ![]() $\Delta f$ is the range of frequencies over which spectral components are defined (made non-dimensional as
$\Delta f$ is the range of frequencies over which spectral components are defined (made non-dimensional as ![]() $\varDelta =\Delta f/f_0$). For constant-amplitude
$\varDelta =\Delta f/f_0$). For constant-amplitude ![]() $a_n=C$ (
$a_n=C$ (![]() $m=0$ in (2.3)) or constant-steepness
$m=0$ in (2.3)) or constant-steepness ![]() $a_nk_n=C$ (
$a_nk_n=C$ (![]() $m=-2$ in (2.3) on deep water) spectra, the bandwidth parameter
$m=-2$ in (2.3) on deep water) spectra, the bandwidth parameter ![]() $\Delta f$ has a well-defined effect on the distribution of wave amplitude (and energy) as a function of frequency. For both spectral shapes, it is possible to define spectra with a wide range of bandwidths (
$\Delta f$ has a well-defined effect on the distribution of wave amplitude (and energy) as a function of frequency. For both spectral shapes, it is possible to define spectra with a wide range of bandwidths (![]() $0<\varDelta <2$).
$0<\varDelta <2$).
2.2.2. JONSWAP spectra
A drawback of using constant-amplitude and constant-steepness spectra is that such simple spectra do not represent well the complete spectral shape of realistic ocean waves. A JONSWAP spectrum,
 \begin{align} \hat{\eta}^{(1)}(f)\propto g^2(2{\rm \pi})^{{-}4}f^{{-}5}\exp\left(-\frac{5}{4}\left(\frac{f}{f_p}\right)^{{-}4}\right)\gamma^\beta \quad \textrm{with}\ \beta=\exp\left(\frac{-(f/f_p-1)^2}{2\sigma^2}\right), \end{align}
\begin{align} \hat{\eta}^{(1)}(f)\propto g^2(2{\rm \pi})^{{-}4}f^{{-}5}\exp\left(-\frac{5}{4}\left(\frac{f}{f_p}\right)^{{-}4}\right)\gamma^\beta \quad \textrm{with}\ \beta=\exp\left(\frac{-(f/f_p-1)^2}{2\sigma^2}\right), \end{align}
provides a more realistic alternative, from which breaking wave groups of different bandwidths may be generated by varying the peak enhancement parameter ![]() $\gamma$. In (2.4),
$\gamma$. In (2.4), ![]() $f_p$ is the peak frequency of the spectrum, and
$f_p$ is the peak frequency of the spectrum, and ![]() $\sigma$ takes the values
$\sigma$ takes the values ![]() $0.07$ and
$0.07$ and ![]() $0.09$ when
$0.09$ when ![]() $f< f_p$ and
$f< f_p$ and ![]() $f>f_p$, respectively. The parametric form of the JONSWAP spectrum in (2.4) generally corresponds to an energy spectrum (and, thus,
$f>f_p$, respectively. The parametric form of the JONSWAP spectrum in (2.4) generally corresponds to an energy spectrum (and, thus, ![]() $a_n\propto \sqrt {E(f_n)}$). Instead, we set the amplitude spectrum to be proportional to the JONSWAP spectrum itself in (2.4), as this gives the correct shape of extreme (and, thus, breaking) waves in an underlying random Gaussian sea (Lindgren Reference Lindgren1970; Boccotti Reference Boccotti1981).
$a_n\propto \sqrt {E(f_n)}$). Instead, we set the amplitude spectrum to be proportional to the JONSWAP spectrum itself in (2.4), as this gives the correct shape of extreme (and, thus, breaking) waves in an underlying random Gaussian sea (Lindgren Reference Lindgren1970; Boccotti Reference Boccotti1981).
2.3. Varying bandwidth for different spectral shapes
For all spectral shapes (i.e. (2.3) and (2.4)), the amplitude of the spectrum ![]() $\hat {\eta }(f)$,
$\hat {\eta }(f)$, ![]() $a_0$, is scaled to achieve the desired global steepness
$a_0$, is scaled to achieve the desired global steepness ![]() $S$ of the corresponding wave group. Varying bandwidth indirectly, using parameters such as
$S$ of the corresponding wave group. Varying bandwidth indirectly, using parameters such as ![]() $\varDelta$, and
$\varDelta$, and ![]() $\gamma$ for a given spectral shape, causes the corresponding mean or characteristic wavenumber,
$\gamma$ for a given spectral shape, causes the corresponding mean or characteristic wavenumber,
to change value. Herein, when comparing wave groups of different bandwidths, we adjust the value of ![]() $f_0$ or
$f_0$ or ![]() $f_p$ to maintain a constant value of
$f_p$ to maintain a constant value of ![]() $k_c$. By keeping constant
$k_c$. By keeping constant ![]() $k_c$, wave groups of equal
$k_c$, wave groups of equal ![]() $S$ are also of equal amplitude, as
$S$ are also of equal amplitude, as ![]() $S\equiv k_c\sum a_n$ with
$S\equiv k_c\sum a_n$ with ![]() $a_0=\sum a_n$. For all wave groups we examine herein, we choose a characteristic frequency of
$a_0=\sum a_n$. For all wave groups we examine herein, we choose a characteristic frequency of ![]() $f_c=1$ Hz (
$f_c=1$ Hz (![]() $T_c=1$ s,
$T_c=1$ s, ![]() $\omega _c=2{\rm \pi} \ {\rm rad}\ {\rm s}^{-1}$, and
$\omega _c=2{\rm \pi} \ {\rm rad}\ {\rm s}^{-1}$, and ![]() $k_c=(2{\rm \pi} )^2/g\ {\rm rad}\ {\rm m}^{-1}$).
$k_c=(2{\rm \pi} )^2/g\ {\rm rad}\ {\rm m}^{-1}$).
Examples of the spectra and resulting focused wave groups we use for linear calculations are shown in figure 3. The colour scales denote the values of parameters ![]() $\varDelta$ and
$\varDelta$ and ![]() $\gamma$ that correspond to the spectra and the wave groups in each panel; the same values and colours are also used in figure 4. We note that the parameters
$\gamma$ that correspond to the spectra and the wave groups in each panel; the same values and colours are also used in figure 4. We note that the parameters ![]() $\varDelta$ and
$\varDelta$ and ![]() $\gamma$ are not direct measures of bandwidth, and varying
$\gamma$ are not direct measures of bandwidth, and varying ![]() $\varDelta$ and
$\varDelta$ and ![]() $\gamma$ also changes other moments such as skewness. In the following sections, to provide a more general discussion on the role of bandwidth, we use the parameter
$\gamma$ also changes other moments such as skewness. In the following sections, to provide a more general discussion on the role of bandwidth, we use the parameter ![]() $\nu$ unless stated otherwise, which is calculated as
$\nu$ unless stated otherwise, which is calculated as ![]() $\sqrt {m_0m_2/m_1^2-1}$ with
$\sqrt {m_0m_2/m_1^2-1}$ with ![]() $m_n$ the
$m_n$ the ![]() $n{\rm th}$ spectral moment of the energy spectrum
$n{\rm th}$ spectral moment of the energy spectrum ![]() $E(f)$.
$E(f)$.

Figure 3. Spectral shapes and corresponding linear focused wave groups used for calculations in figure 4; (a,d) constant-amplitude, (b,e) constant-steepness and (c, f) JONSWAP spectra. Bandwidth is varied using the parameters ![]() $\Delta f$ (panels a,b,d,e) and
$\Delta f$ (panels a,b,d,e) and ![]() $\gamma$ (panel c, f); the colour scales denote the corresponding values of
$\gamma$ (panel c, f); the colour scales denote the corresponding values of ![]() $\varDelta$ (constant amplitude and constant steepness) and
$\varDelta$ (constant amplitude and constant steepness) and ![]() $\gamma$ (JONSWAP).
$\gamma$ (JONSWAP).

Figure 4. Focused wave crest kinematics and measures of surface slope plotted as a function of bandwidth ![]() $\nu$, calculated based on linear theory at time and position of linear focus (
$\nu$, calculated based on linear theory at time and position of linear focus (![]() $t=0, x=0$), for wave groups based on constant-amplitude (filled grey markers), constant-steepness (open grey markers) and JONSWAP spectra (filled coloured markers). The colour scales denote the corresponding values of
$t=0, x=0$), for wave groups based on constant-amplitude (filled grey markers), constant-steepness (open grey markers) and JONSWAP spectra (filled coloured markers). The colour scales denote the corresponding values of ![]() $\gamma$ (JONSWAP) and
$\gamma$ (JONSWAP) and ![]() $\varDelta$ (constant amplitude and constant steepness).
$\varDelta$ (constant amplitude and constant steepness).
3. Linear predictions of surface kinematics and slope
For waves with narrow-banded underlying spectra, nonlinear focusing brought about by third-order quasi-resonant wave–wave interactions (modulational instability) causes the formation of large waves that may eventually lead to breaking. Modulated wave trains with low initial monochromatic steepness (IMS, ![]() $a_0k_0>0.08$) may evolve to breaking given sufficient time (Dold & Peregrine Reference Dold and Peregrine1986b; Babanin et al. Reference Babanin, Chalikov, Young and Savelyev2010). The local steepness, as waves approach breaking, tends to a value of
$a_0k_0>0.08$) may evolve to breaking given sufficient time (Dold & Peregrine Reference Dold and Peregrine1986b; Babanin et al. Reference Babanin, Chalikov, Young and Savelyev2010). The local steepness, as waves approach breaking, tends to a value of ![]() $kH/2=0.44$ for waves generated in this manner (Babanin et al. Reference Babanin, Chalikov, Young and Savelyev2010). For waves with broad underlying spectra, however, the role of nonlinear focusing is reduced, and linear approximations may provided reasonable predictions of surface kinematics and slope. We revisit this with fully nonlinear simulations in § 4.
$kH/2=0.44$ for waves generated in this manner (Babanin et al. Reference Babanin, Chalikov, Young and Savelyev2010). For waves with broad underlying spectra, however, the role of nonlinear focusing is reduced, and linear approximations may provided reasonable predictions of surface kinematics and slope. We revisit this with fully nonlinear simulations in § 4.
In the following section we use linear wave theory to calculate approximate values of surface kinematics and slope to better understand how bandwidth and spectral shape may affect breaking onset. For all the wave groups in this section, the same value of global wave steepness ![]() $S=1$ is maintained.
$S=1$ is maintained.
3.1. Surface kinematics
The kinematic description of wave breaking, which makes use of the ratio of fluid velocity to crest speed, provides an intuitive means to explore the effects bandwidth and spectral shape may have on breaking onset. Following kinematic arguments, wave breaking occurs when the fluid velocity at a wave crest reaches or exceeds the crests velocity. The ratio of fluid velocity to crest speed is also the basis for the parameter ![]() $B_x$, which was derived using dynamical arguments in Barthelemy et al. (Reference Barthelemy, Banner, Peirson, Fedele, Allis and Dias2018), and has been shown to predict the onset of breaking for 2-D (Saket et al. Reference Saket, Peirson, Banner, Barthelemy and Allis2017) and moderately spread waves (Barthelemy et al. Reference Barthelemy, Banner, Peirson, Fedele, Allis and Dias2018) in a range of water depths (Derakhti et al. Reference Derakhti, Kirby, Banner, Grilli and Thomson2020). In these studies, breaking occurs when
$B_x$, which was derived using dynamical arguments in Barthelemy et al. (Reference Barthelemy, Banner, Peirson, Fedele, Allis and Dias2018), and has been shown to predict the onset of breaking for 2-D (Saket et al. Reference Saket, Peirson, Banner, Barthelemy and Allis2017) and moderately spread waves (Barthelemy et al. Reference Barthelemy, Banner, Peirson, Fedele, Allis and Dias2018) in a range of water depths (Derakhti et al. Reference Derakhti, Kirby, Banner, Grilli and Thomson2020). In these studies, breaking occurs when ![]() $B_x>0.855$. Therefore, we use the parameter
$B_x>0.855$. Therefore, we use the parameter ![]() $B_x$ to refer to the ratio of fluid to crest speed hereafter. In the following section we use linear wave theory to examine how bandwidth affects wave crest kinematics and, thus, the ratio of fluid to crest speed
$B_x$ to refer to the ratio of fluid to crest speed hereafter. In the following section we use linear wave theory to examine how bandwidth affects wave crest kinematics and, thus, the ratio of fluid to crest speed ![]() $B_x$.
$B_x$.
3.1.1. Crest speed
The dispersive nature of surface gravity waves causes the apparent crest speed of an unsteady wave group to fluctuate as wave components of varying phase speeds interact, coming in and out of phase (Fedele, Banner & Barthelemy Reference Fedele, Banner and Barthelemy2020). This effect has been observed in field data, and crest slow-down in particular has been linked to breaking onset (Banner et al. Reference Banner, Barthelemy, Fedele, Allis, Benetazzo, Dias and Peirson2014). Crest speed fluctuation is a predominantly linear effect that is also affected by nonlinear changes to dispersion as waves become steeper (Fedele et al. Reference Fedele, Banner and Barthelemy2020). The degree to which crest speed varies is related to the bandwidth of the underlying spectrum, as is the degree to which nonlinearity will affect dispersion. Two-dimensional wave groups with broad underlying spectra will experience greater linear crest speed variation and reduced nonlinear dispersion.
If we define a crest as the point at which slope ![]() $\partial \eta /\partial x=0$, which occurs at
$\partial \eta /\partial x=0$, which occurs at ![]() $x=x_c(t)$, crest speed
$x=x_c(t)$, crest speed ![]() $C^{(1)}\equiv {\rm d}\kern 0.06em x_c/{\rm d} t$, where the superscript denotes this is a linear approximation. For a discrete spectrum of
$C^{(1)}\equiv {\rm d}\kern 0.06em x_c/{\rm d} t$, where the superscript denotes this is a linear approximation. For a discrete spectrum of ![]() $N$ waves at linear focus (
$N$ waves at linear focus (![]() $x=0$,
$x=0$, ![]() $t=0$), this may be expressed as
$t=0$), this may be expressed as
 \begin{equation} C^{(1)}=\frac{\sum_{n=1}^{N}a_{n}\omega_nk_n}{\sum_{n=1}^{N}a_{n}k_n^2}. \end{equation}
\begin{equation} C^{(1)}=\frac{\sum_{n=1}^{N}a_{n}\omega_nk_n}{\sum_{n=1}^{N}a_{n}k_n^2}. \end{equation} Linearly predicted crest speed, normalised by characteristic phase speed ![]() $C_c$, is shown as a function of bandwidth
$C_c$, is shown as a function of bandwidth ![]() $\nu$ in figure 4(a) for the three different spectral shapes we examine. We use characteristic wavenumber (defined in (2.5)) and frequency to calculate characteristic phase speed:
$\nu$ in figure 4(a) for the three different spectral shapes we examine. We use characteristic wavenumber (defined in (2.5)) and frequency to calculate characteristic phase speed: ![]() $C_c=\omega _c/k_c$. For all three spectral shapes, crest speed reduces with increasing bandwidth (note that the normalisation by
$C_c=\omega _c/k_c$. For all three spectral shapes, crest speed reduces with increasing bandwidth (note that the normalisation by ![]() $C_c$ is independent of bandwidth, as we maintain a constant value of
$C_c$ is independent of bandwidth, as we maintain a constant value of ![]() $k_c$). For the JONSWAP spectra, which extend over a smaller range of bandwidths
$k_c$). For the JONSWAP spectra, which extend over a smaller range of bandwidths ![]() $\nu$, the rate of crest slow down is similar to the constant-amplitude spectra, but the normalised values of crest speed are much lower. This difference is a result of the high-frequency tail of the JONSWAP spectrum.
$\nu$, the rate of crest slow down is similar to the constant-amplitude spectra, but the normalised values of crest speed are much lower. This difference is a result of the high-frequency tail of the JONSWAP spectrum.
3.1.2. Fluid velocity
Horizontal fluid velocity at ![]() $z=0$ and at focus (
$z=0$ and at focus (![]() $x=0, t=0$) may be calculated linearly for a discrete spectrum of
$x=0, t=0$) may be calculated linearly for a discrete spectrum of ![]() $N$ waves as
$N$ waves as
 \begin{equation} u^{(1)}=\left.\frac{\partial\phi^{(1)}}{\partial x}\right|_{x=0, z=0, t=0}=\sum_{n=1}^{N}a_{n}\omega_n. \end{equation}
\begin{equation} u^{(1)}=\left.\frac{\partial\phi^{(1)}}{\partial x}\right|_{x=0, z=0, t=0}=\sum_{n=1}^{N}a_{n}\omega_n. \end{equation}
Although evidently lower than the (nonlinear) velocity at the crest of a wave (![]() $z=\eta$), linear fluid velocity at
$z=\eta$), linear fluid velocity at ![]() $z=0$ can still be used to illustrate how bandwidth affects surface kinematics.
$z=0$ can still be used to illustrate how bandwidth affects surface kinematics.
Linearly predicted horizontal fluid velocity, normalised by characteristic velocity ![]() $a_0 \omega _c$ (constant as
$a_0 \omega _c$ (constant as ![]() $\nu$ is varied), are plotted as a function of bandwidth
$\nu$ is varied), are plotted as a function of bandwidth ![]() $\nu$ for the different spectral shapes we examine in figure 4(b). As bandwidth is increased, fluid velocity reduces in similar manner to crest speed, but to a lesser extent.
$\nu$ for the different spectral shapes we examine in figure 4(b). As bandwidth is increased, fluid velocity reduces in similar manner to crest speed, but to a lesser extent.
3.1.3. Kinematic breaking parameter
For all three spectral shapes ![]() $B_x^{(1)}\equiv u^{(1)}/C^{(1)}$ increases as a function of bandwidth, as shown in figure 4(c). This implies that for a certain value of global steepness
$B_x^{(1)}\equiv u^{(1)}/C^{(1)}$ increases as a function of bandwidth, as shown in figure 4(c). This implies that for a certain value of global steepness ![]() $S$, which is kept constant as bandwidth is varied in our calculations, waves of broader bandwidth are more likely to break. In other words, linear wave theory suggests breaking (if it occurs a fixed value of
$S$, which is kept constant as bandwidth is varied in our calculations, waves of broader bandwidth are more likely to break. In other words, linear wave theory suggests breaking (if it occurs a fixed value of ![]() $B_x^{(1)}$) will occur at lower global steepness for wave groups with broader underlying spectra.
$B_x^{(1)}$) will occur at lower global steepness for wave groups with broader underlying spectra.
3.2. Steepness and wave slope
For a discrete spectrum of ![]() $N$ waves, linear surface slope is given by
$N$ waves, linear surface slope is given by
 \begin{equation} \eta^{(1)}_x=\frac{\partial\eta^{(1)}}{\partial x}=\sum^N_{n=1}-a_n k_n \sin(\theta_n). \end{equation}
\begin{equation} \eta^{(1)}_x=\frac{\partial\eta^{(1)}}{\partial x}=\sum^N_{n=1}-a_n k_n \sin(\theta_n). \end{equation}
Global steepness ![]() $S$ is the maximum possible value of linear surface slope,
$S$ is the maximum possible value of linear surface slope,
 \begin{equation} S=\sum_{n=1}^{N}a_{n}k_n\equiv k_c\sum_{n=1}^{N}a_{n}\equiv a_0 k_c, \end{equation}
\begin{equation} S=\sum_{n=1}^{N}a_{n}k_n\equiv k_c\sum_{n=1}^{N}a_{n}\equiv a_0 k_c, \end{equation}
which is realised when the phases ![]() $\theta _n$ of all wave components are simultaneously
$\theta _n$ of all wave components are simultaneously ![]() ${\rm \pi} /2$. This global steepness
${\rm \pi} /2$. This global steepness ![]() $S$ is used to parameterise a range of breaking-related phenomena such as breaking intensity (Drazen, Melville & Lenain Reference Drazen, Melville and Lenain2008). Pizzo & Melville (Reference Pizzo and Melville2019) and Pizzo et al. (Reference Pizzo, Murray, Smith and Lenain2021) demonstrate, when paired with
$S$ is used to parameterise a range of breaking-related phenomena such as breaking intensity (Drazen, Melville & Lenain Reference Drazen, Melville and Lenain2008). Pizzo & Melville (Reference Pizzo and Melville2019) and Pizzo et al. (Reference Pizzo, Murray, Smith and Lenain2021) demonstrate, when paired with ![]() $\varDelta$, the global (or spectral) measure of steepness
$\varDelta$, the global (or spectral) measure of steepness ![]() $S$ functions well as a parameter to predict breaking onset for chirped wave groups and wave groups based on a constant-steepness spectra (cf. (1.2)). In these studies, the parameter
$S$ functions well as a parameter to predict breaking onset for chirped wave groups and wave groups based on a constant-steepness spectra (cf. (1.2)). In these studies, the parameter ![]() $S$ functions as a global measure of nonlinearity (steepness) and
$S$ functions as a global measure of nonlinearity (steepness) and ![]() $\varDelta$ as a measure of the degree to which dispersion or nonlinear focusing will occur (bandwidth).
$\varDelta$ as a measure of the degree to which dispersion or nonlinear focusing will occur (bandwidth).
By definition, linear waves have the property ![]() $\mathrm {max}(|\eta ^{(1)}_x|)=\mathrm {max}(\eta ^{(1)}_x)=-\mathrm {min}(\eta ^{(1)}_x)$, which is not necessarily true for nonlinear waves, for which
$\mathrm {max}(|\eta ^{(1)}_x|)=\mathrm {max}(\eta ^{(1)}_x)=-\mathrm {min}(\eta ^{(1)}_x)$, which is not necessarily true for nonlinear waves, for which ![]() $\mathrm {max}(\eta _x)\neq -\mathrm {min}(\eta _x)$. Wave breaking is initiated by overturning and crest instabilities that occur at the crest front, and hence when referring to maximum local slope we report
$\mathrm {max}(\eta _x)\neq -\mathrm {min}(\eta _x)$. Wave breaking is initiated by overturning and crest instabilities that occur at the crest front, and hence when referring to maximum local slope we report ![]() $|\mathrm {min}(\eta _x)|$. Nonlinearity, phase coherence, and imperfect wave generation may mean that actual wave slope at the point of wave breaking (local) will differ from a global measure such as
$|\mathrm {min}(\eta _x)|$. Nonlinearity, phase coherence, and imperfect wave generation may mean that actual wave slope at the point of wave breaking (local) will differ from a global measure such as ![]() $S$. To generate a (crest-)focused wave group, the phases of wave components are selected such that
$S$. To generate a (crest-)focused wave group, the phases of wave components are selected such that ![]() $k_nx-\omega _n t+\varphi _n=0$ at
$k_nx-\omega _n t+\varphi _n=0$ at ![]() $t=0$ and
$t=0$ and ![]() $x=0$. To generate a maximum steepness wave group, the phases of all wave components
$x=0$. To generate a maximum steepness wave group, the phases of all wave components ![]() $(k_nx-\omega _n t+\varphi _n)$ must be equal to
$(k_nx-\omega _n t+\varphi _n)$ must be equal to ![]() ${\rm \pi} /2$. These two conditions are evidently incompatible, except for monochromatic waves, and thus maximum local slope
${\rm \pi} /2$. These two conditions are evidently incompatible, except for monochromatic waves, and thus maximum local slope ![]() $|\mathrm {min}(\eta ^{(1)}_x)|$ will only tend to
$|\mathrm {min}(\eta ^{(1)}_x)|$ will only tend to ![]() $S$ as
$S$ as ![]() $\nu \rightarrow 0$. In figure 4(d),
$\nu \rightarrow 0$. In figure 4(d), ![]() $|\mathrm {min}(\eta ^{(1)}_x)|$ is plotted as a function of bandwidth. The difference between
$|\mathrm {min}(\eta ^{(1)}_x)|$ is plotted as a function of bandwidth. The difference between ![]() $|\mathrm {min}(\eta ^{(1)}_x)|$ and
$|\mathrm {min}(\eta ^{(1)}_x)|$ and ![]() $S$ (which we set to 1) increases with bandwidth and is more significant for the JONSWAP spectra. For all three spectral shapes and all values of
$S$ (which we set to 1) increases with bandwidth and is more significant for the JONSWAP spectra. For all three spectral shapes and all values of ![]() $\nu$, the difference between local (
$\nu$, the difference between local (![]() $|\mathrm {min}(\eta ^{(1)}_x)|$) and global steepness (
$|\mathrm {min}(\eta ^{(1)}_x)|$) and global steepness (![]() $S$) is less than
$S$) is less than ![]() $10\,\%$.
$10\,\%$.
In Wu & Yao (Reference Wu and Yao2004) and many other studies, local steepness ![]() $kH/2$, where
$kH/2$, where ![]() $H$ is wave height and
$H$ is wave height and ![]() $k$ is wavenumber (based on some local measure of period
$k$ is wavenumber (based on some local measure of period ![]() $T$ or wavelength
$T$ or wavelength ![]() $\lambda$), is used to examine wave breaking onset. Wu & Yao (Reference Wu and Yao2004) show that
$\lambda$), is used to examine wave breaking onset. Wu & Yao (Reference Wu and Yao2004) show that ![]() $kH/2$ functions well as parameter to predict the onset of wave breaking for wave groups based on constant-steepness and constant-amplitude spectra (cf. (1.1)). As introduced in § 1, the parameterisations (1.2) and (1.1) (from Pizzo et al. (Reference Pizzo, Murray, Smith and Lenain2021) and Wu & Yao (Reference Wu and Yao2004), respectively) describe opposing relationships between bandwidth and breaking steepness. In figure 4(e) linearly calculated local wave steepness
$kH/2$ functions well as parameter to predict the onset of wave breaking for wave groups based on constant-steepness and constant-amplitude spectra (cf. (1.1)). As introduced in § 1, the parameterisations (1.2) and (1.1) (from Pizzo et al. (Reference Pizzo, Murray, Smith and Lenain2021) and Wu & Yao (Reference Wu and Yao2004), respectively) describe opposing relationships between bandwidth and breaking steepness. In figure 4(e) linearly calculated local wave steepness ![]() $kH^{(1)}/2$ is plotted as a function of bandwidth; as bandwidth increases,
$kH^{(1)}/2$ is plotted as a function of bandwidth; as bandwidth increases, ![]() $kH^{(1)}/2$ decreases for all three spectral shapes. Both wave local wavenumber
$kH^{(1)}/2$ decreases for all three spectral shapes. Both wave local wavenumber ![]() $k$ and height
$k$ and height ![]() $H^{(1)}$ decrease as a function of bandwidth (cf. figures 4( f) and 4(g), respectively). For constant-amplitude spectra the decreases in
$H^{(1)}$ decrease as a function of bandwidth (cf. figures 4( f) and 4(g), respectively). For constant-amplitude spectra the decreases in ![]() $kH^{(1)}/2$ is not smooth; this is a result of jumps in the position of zero-crossings that are used to calculate local wavenumber
$kH^{(1)}/2$ is not smooth; this is a result of jumps in the position of zero-crossings that are used to calculate local wavenumber ![]() $k$ (figure 4f). Vertical asymmetry that arises from finite bandwidth, which causes
$k$ (figure 4f). Vertical asymmetry that arises from finite bandwidth, which causes ![]() $H^{(1)}$ to decrease, is a well-established linear effect (e.g. Boccotti Reference Boccotti1981). This local measure of steepness
$H^{(1)}$ to decrease, is a well-established linear effect (e.g. Boccotti Reference Boccotti1981). This local measure of steepness ![]() $kH^{(1)}/2$ varies by as much as
$kH^{(1)}/2$ varies by as much as ![]() $80\,\%$ as bandwidth is increased in figure 4(e), whereas local slope
$80\,\%$ as bandwidth is increased in figure 4(e), whereas local slope ![]() $|\mathrm {min}(\eta ^{(1)}_x)|$ varies only by 4 %–10 % in figure 4(d) (for wave groups of constant
$|\mathrm {min}(\eta ^{(1)}_x)|$ varies only by 4 %–10 % in figure 4(d) (for wave groups of constant ![]() $S$).
$S$).
The reduction in local steepness with bandwidth we predict using linear wave theory can, at least partially, explain the behaviour of (1.1) and, thus, the perceived conflicting relationships between breaking onset and bandwidth reported in Pizzo et al. (Reference Pizzo, Murray, Smith and Lenain2021) and Wu & Yao (Reference Wu and Yao2004). We note that in our calculations ![]() $H^{(1)}$ and
$H^{(1)}$ and ![]() $k$ are calculated spatially, using zero-crossing methods, and in Wu & Yao (Reference Wu and Yao2004) the same values are calculated using time-domain measurements, and the linear dispersion relationship is used to calculate
$k$ are calculated spatially, using zero-crossing methods, and in Wu & Yao (Reference Wu and Yao2004) the same values are calculated using time-domain measurements, and the linear dispersion relationship is used to calculate ![]() $k$ from the zero-crossing period. Even for linear calculations there is a degree of error associated with this method used in Wu & Yao (Reference Wu and Yao2004). In addition, in Wu & Yao (Reference Wu and Yao2004) measurements were only made at locations where a wave gauge was located, which is not necessarily the location of the maximum local steepness (this is an issue for all experiments where wave gauge measurements are used). Rapp & Melville (Reference Rapp and Melville1990) also report that for experimentally generated incipient breaking waves, local steepness decreased with bandwidth and global steepness stayed approximately constant (
$k$ from the zero-crossing period. Even for linear calculations there is a degree of error associated with this method used in Wu & Yao (Reference Wu and Yao2004). In addition, in Wu & Yao (Reference Wu and Yao2004) measurements were only made at locations where a wave gauge was located, which is not necessarily the location of the maximum local steepness (this is an issue for all experiments where wave gauge measurements are used). Rapp & Melville (Reference Rapp and Melville1990) also report that for experimentally generated incipient breaking waves, local steepness decreased with bandwidth and global steepness stayed approximately constant (![]() $a_{sb}k_c$ and
$a_{sb}k_c$ and ![]() $ak_c$ in their notation, respectively). For these experiments focused wave groups were generated using constant-amplitude spectra; this different spectral shape may be a reason why
$ak_c$ in their notation, respectively). For these experiments focused wave groups were generated using constant-amplitude spectra; this different spectral shape may be a reason why ![]() $S$ remained approximately constant and did not increase with bandwidth as observed in Pizzo & Melville (Reference Pizzo and Melville2019).
$S$ remained approximately constant and did not increase with bandwidth as observed in Pizzo & Melville (Reference Pizzo and Melville2019).
4. Fully nonlinear numerical simulations
In two dimensions, third-order quasi-resonant wave–wave interactions lead to modulational instability or nonlinear focusing when steepness ![]() $S$ is high and bandwidth is low. In such cases, nonlinear focusing may lead to large deviations from linear wave theory.
$S$ is high and bandwidth is low. In such cases, nonlinear focusing may lead to large deviations from linear wave theory.
In the following section, we perform numerical simulations using a fully nonlinear boundary integral method (Dold & Peregrine Reference Dold and Peregrine1986a) to examine how bandwidth and spectral shape may influence breaking onset. The numerical model is mixed Eulerian–Lagrangian and allows for the simulation of double-valued surfaces to the point of reconnection. Therefore, we can simulate breaking waves, and in what follows we identify breaking onset to occur when the free surface becomes vertical. The numerical method has been widely used and validated in similar studies (e.g. Dold Reference Dold1992; Henderson, Peregrine & Dold Reference Henderson, Peregrine and Dold1999; Song & Banner Reference Song and Banner2002; Pizzo & Melville Reference Pizzo and Melville2019; Pizzo et al. Reference Pizzo, Murray, Smith and Lenain2021).
We first explain the numerical domain and initial conditions we use to perform simulations (§ 4.1), we then investigate global and local measures of steepness using simulations based on constant-steepness spectra (§ 4.2), and finally investigate spectral shape (§ 4.4) and breaking onset detection (§ 4.5) using simulations based on constant-steepness, constant-amplitude and JONSWAP spectra.
4.1. Numerical method
The numerical method we use (Dold & Peregrine Reference Dold and Peregrine1986a) solves Laplace's equation subject to the kinematic and dynamic boundary conditions for free surface gravity waves in deep water, using an approach based on Cauchy's integral formula. This approach describes the time evolution of Lagrangian surface particles in a conformally mapped frame and is computationally efficient compared to boundary integral methods that are solved in the physical domain. The potential-flow simulations we perform do not account for the effects of surface tension and viscosity and, thus, relate only to purely gravity-driven surface waves and wave breaking.
4.1.1. Domain set-up
In defining the scale of our numerical domain we use similar parameters to those used in Pizzo et al. (Reference Pizzo, Murray, Smith and Lenain2021); these are summarised in table 2. The initial length of the domain, at ![]() $t_0$ (we use the subscript
$t_0$ (we use the subscript ![]() $0$ to indicate initial values),
$0$ to indicate initial values), ![]() $X=93.7$ m, which corresponds to
$X=93.7$ m, which corresponds to ![]() $60$ characteristic wavelengths (
$60$ characteristic wavelengths (![]() $\lambda _c=2{\rm \pi} /k_c$). For the simulations we present the domain is discretised using
$\lambda _c=2{\rm \pi} /k_c$). For the simulations we present the domain is discretised using ![]() $2048$ particles, giving an initial particle spacing
$2048$ particles, giving an initial particle spacing ![]() $\varDelta _{X_0}$ of
$\varDelta _{X_0}$ of ![]() $4.6$ cm, which corresponds to approximately
$4.6$ cm, which corresponds to approximately ![]() $34$ particles per wavelength (Configuration A).
$34$ particles per wavelength (Configuration A).
Table 2. Numerical domain set-up.

For a number of simulations we apply a conformal map (Pizzo & Melville Reference Pizzo and Melville2019) to redistribute particles so that they are clustered around the focused wave group one period prior to the time of wave breaking ![]() $t^\star$ (Configuration B). The initial particle positions
$t^\star$ (Configuration B). The initial particle positions ![]() $x_p$ are projected onto a unit circle
$x_p$ are projected onto a unit circle ![]() $\zeta =\exp ({\rm i}2{\rm \pi} x_p/X)$ and then remapped,
$\zeta =\exp ({\rm i}2{\rm \pi} x_p/X)$ and then remapped,
where ![]() $\nu _0$ defines the degree of clustering. For the simulations we rerun using this mapping a value of
$\nu _0$ defines the degree of clustering. For the simulations we rerun using this mapping a value of ![]() $\nu _0=-0.5$ was used. This remapping gives a minimum particle spacing of
$\nu _0=-0.5$ was used. This remapping gives a minimum particle spacing of ![]() $1.5$ cm or approximately
$1.5$ cm or approximately ![]() $105$ particles per wavelength.
$105$ particles per wavelength.
4.1.2. Initial conditions
The numerical domain is periodic in space and models the time evolution of Lagrangian particles located on the free surface. Simulations are initialised using initial conditions in the form of a potential at each initial particle location (at the free surface). Initial particle spacing in ![]() $x$ may be defined arbitrarily and need not be regular. The smallest particle spacing affects the model's high-wavenumber resolution. We define our initial particle spacing regularly as
$x$ may be defined arbitrarily and need not be regular. The smallest particle spacing affects the model's high-wavenumber resolution. We define our initial particle spacing regularly as ![]() $\varDelta _{X_0}=X/N_p$, where
$\varDelta _{X_0}=X/N_p$, where ![]() $N_p$ is the number of particles.
$N_p$ is the number of particles.
We define initial conditions using linear wave theory (see § 2). To reduce errors associated with using these approximate initial conditions, we choose a start time ![]() $t_0$ that ensures the waves are dispersed and have low initial steepness. The time required to achieve this varies with bandwidth; we thus define initial time as
$t_0$ that ensures the waves are dispersed and have low initial steepness. The time required to achieve this varies with bandwidth; we thus define initial time as ![]() $t_0=-L/(\nu C_{gc})$ (akin to Pizzo et al. Reference Pizzo, Murray, Smith and Lenain2021), where
$t_0=-L/(\nu C_{gc})$ (akin to Pizzo et al. Reference Pizzo, Murray, Smith and Lenain2021), where ![]() $C_{gc}=\omega _c/(2k_c)$ is the characteristic group velocity in deep water and
$C_{gc}=\omega _c/(2k_c)$ is the characteristic group velocity in deep water and ![]() $L=10$ m is an arbitrary distance. Defining our initial particle distribution as uniformly spaced in
$L=10$ m is an arbitrary distance. Defining our initial particle distribution as uniformly spaced in ![]() $x$ results in a wavenumber discretisation of
$x$ results in a wavenumber discretisation of ![]() $k_n=n 2{\rm \pi} /X$ for
$k_n=n 2{\rm \pi} /X$ for ![]() $n=1$ to
$n=1$ to ![]() $N_p/2$. Initial conditions are scaled to give the desired value of
$N_p/2$. Initial conditions are scaled to give the desired value of ![]() $S$ at linear focus (see also § 2). For JONSWAP spectra the finite wavenumber support results in a slight truncation of the high-frequency tail (at approximately
$S$ at linear focus (see also § 2). For JONSWAP spectra the finite wavenumber support results in a slight truncation of the high-frequency tail (at approximately ![]() $17k_c$ or
$17k_c$ or ![]() $4f_c$, which is
$4f_c$, which is ![]() $6f_p$). Each simulation is run for a total time of
$6f_p$). Each simulation is run for a total time of ![]() $T=1.25|t_0|$. The time step of the model is defined dynamically to maintain a specified order of accuracy.
$T=1.25|t_0|$. The time step of the model is defined dynamically to maintain a specified order of accuracy.
4.2. Global and local measures of steepness
In § 3 we have demonstrated that, for wave groups of constant global steepness ![]() $S$, local steepness at focus (
$S$, local steepness at focus (![]() $kH/2$) decreases with bandwidth. We now examine how significantly this linearly predicted phenomenon affects nonlinear breaking waves by simulating incipient breaking wave groups based on constant-steepness spectra. To produce simulations of incipient breaking waves for a range of bandwidths, we search for the steepest non-breaking wave group at each value of bandwidth by varying the input value of
$kH/2$) decreases with bandwidth. We now examine how significantly this linearly predicted phenomenon affects nonlinear breaking waves by simulating incipient breaking wave groups based on constant-steepness spectra. To produce simulations of incipient breaking waves for a range of bandwidths, we search for the steepest non-breaking wave group at each value of bandwidth by varying the input value of ![]() $S$. We make use of (1.2) to provide an initial guess of this value of
$S$. We make use of (1.2) to provide an initial guess of this value of ![]() $S$. We stop searching when the step size in
$S$. We stop searching when the step size in ![]() $S$ is less than
$S$ is less than ![]() $5\times 10^{-4}$.
$5\times 10^{-4}$.
Figure 5 shows global and local measures of steepness and slope for the largest non-breaking (grey large markers) and smallest breaking wave groups (red small markers) simulated. In all simulations where wave breaking occurred, we limit our search for maximum values of steepness to times prior to the surface becoming double valued. In panel (a) global steepness ![]() $S$ is plotted as a function of
$S$ is plotted as a function of ![]() $\nu$; the input global steepness
$\nu$; the input global steepness ![]() $S$ of simulations involving incipient breaking waves follows the quadratic fit (1.2) of Pizzo et al. (Reference Pizzo, Melville and Deike2019), as expected. The corresponding values of local steepness
$S$ of simulations involving incipient breaking waves follows the quadratic fit (1.2) of Pizzo et al. (Reference Pizzo, Melville and Deike2019), as expected. The corresponding values of local steepness ![]() $kH/2$ are shown in figure 5(b), and are similar though not equivalent to the fit (1.1) of Wu & Yao (Reference Wu and Yao2004) with a clear offset between the two. The difference between the trends in our simulated results shown in panels (a,b) is consistent with the conclusions we have already drawn through linear calculations in § 3. Linear wave theory can therefore explain the difference between (1.1) and (1.2) and help understand inconsistencies in the existing literature (cf. figure 2).
$kH/2$ are shown in figure 5(b), and are similar though not equivalent to the fit (1.1) of Wu & Yao (Reference Wu and Yao2004) with a clear offset between the two. The difference between the trends in our simulated results shown in panels (a,b) is consistent with the conclusions we have already drawn through linear calculations in § 3. Linear wave theory can therefore explain the difference between (1.1) and (1.2) and help understand inconsistencies in the existing literature (cf. figure 2).

Figure 5. Global and local measures of maximum steepness as a function of bandwidth for the steepest non-breaking (grey markers) and least steep breaking (red dots) wave groups based on constant-steepness spectra. In panel (b) closed markers correspond to steepness measured ![]() $\pm T_c/2$ either side of the time of maximum slope
$\pm T_c/2$ either side of the time of maximum slope ![]() $|\mathrm {min}(\eta _x)|$, and open markers correspond to maxima observed without this time constraint; in panel (c) the smaller dark grey dots correspond to simulations that were rerun using increased particle resolution at the crest (Configuration B). The inset in panel (c) shows the (much higher) values of maximum slope of breaking wave groups.
$|\mathrm {min}(\eta _x)|$, and open markers correspond to maxima observed without this time constraint; in panel (c) the smaller dark grey dots correspond to simulations that were rerun using increased particle resolution at the crest (Configuration B). The inset in panel (c) shows the (much higher) values of maximum slope of breaking wave groups.
We note that a degree of conditioning was required to produce the values of ![]() $kH/2$ shown in figure 5(b). The values of
$kH/2$ shown in figure 5(b). The values of ![]() $kH/2$ shown as solid grey dots are the maximum values observed within
$kH/2$ shown as solid grey dots are the maximum values observed within ![]() $\pm T_c/2$ of the time of maximum slope
$\pm T_c/2$ of the time of maximum slope ![]() $|\mathrm {min}(\eta _x)|$. The open markers show the unconstrained maximum values of
$|\mathrm {min}(\eta _x)|$. The open markers show the unconstrained maximum values of ![]() $kH/2$ measured at any time during each simulation, which show considerably more scatter. Estimating wavenumber using zero-crossings is unstable and can cause large spikes in corresponding values of
$kH/2$ measured at any time during each simulation, which show considerably more scatter. Estimating wavenumber using zero-crossings is unstable and can cause large spikes in corresponding values of ![]() $kH/2$. This is further illustrated in figure 6, where in panel (a) up- and down-crossing steepness of the largest wave is plotted as a function of time alongside maximum surface slope
$kH/2$. This is further illustrated in figure 6, where in panel (a) up- and down-crossing steepness of the largest wave is plotted as a function of time alongside maximum surface slope ![]() $|\mathrm {min}(\eta _x)|$. The surface elevations that correspond to the maximum values of each parameter, indicated by the vertical dashed lines in figure 6(a), are plotted in figure 6(b) with zero-crossings shown as
$|\mathrm {min}(\eta _x)|$. The surface elevations that correspond to the maximum values of each parameter, indicated by the vertical dashed lines in figure 6(a), are plotted in figure 6(b) with zero-crossings shown as ![]() $\times$ symbols. Spikes in
$\times$ symbols. Spikes in ![]() $kH/2$ correspond to instances where the free surface forms a wave with two zero-crossings within close proximity, leading to a very short wavelength and large
$kH/2$ correspond to instances where the free surface forms a wave with two zero-crossings within close proximity, leading to a very short wavelength and large ![]() $k$.
$k$.

Figure 6. Example of spikes in local steepness ![]() $kH/2$ calculated for a focusing wave group: (a) up-crossing (
$kH/2$ calculated for a focusing wave group: (a) up-crossing (![]() $k_u H_u/2$) and down-crossing (
$k_u H_u/2$) and down-crossing (![]() $k_d H_d/2$) steepness and maximum local slope of the largest wave as a function of time; (b) the surface elevations that correspond to maximum values of each parameter (of corresponding line colour) with zero-crossings shown as
$k_d H_d/2$) steepness and maximum local slope of the largest wave as a function of time; (b) the surface elevations that correspond to maximum values of each parameter (of corresponding line colour) with zero-crossings shown as ![]() $\times$ symbols. Vertical dashed lines in panel (a) show the three times at which maximum values of each parameter is observed, which correspond to the times for which surface elevations in space are shown in (b).
$\times$ symbols. Vertical dashed lines in panel (a) show the three times at which maximum values of each parameter is observed, which correspond to the times for which surface elevations in space are shown in (b).
Locally measured maximum surface slope ![]() $|\mathrm {min}(\eta _x)|$, shown in figure 5(c), does not vary significantly as a function of bandwidth for the largest non-breaking waves (large grey dots). This may suggest that, independent of bandwidth, breaking is triggered by a maximum value of local slope, which is consistent with the rational presented in Pizzo & Melville (Reference Pizzo and Melville2019).
$|\mathrm {min}(\eta _x)|$, shown in figure 5(c), does not vary significantly as a function of bandwidth for the largest non-breaking waves (large grey dots). This may suggest that, independent of bandwidth, breaking is triggered by a maximum value of local slope, which is consistent with the rational presented in Pizzo & Melville (Reference Pizzo and Melville2019).
The values of ![]() $S$ for breaking waves are all slightly larger than those for the largest non-breaking waves (figure 5a); this is expected as
$S$ for breaking waves are all slightly larger than those for the largest non-breaking waves (figure 5a); this is expected as ![]() $S$ is the independent variable we varied in our search for the breaking threshold. Some values of local steepness
$S$ is the independent variable we varied in our search for the breaking threshold. Some values of local steepness ![]() $kH/2$ are smaller for breaking than they are for non-breaking waves (figure 5b), making it a less useful threshold parameter (in the Appendix we show that this is also the case for various other local steepness parameters). Finally, for local slope
$kH/2$ are smaller for breaking than they are for non-breaking waves (figure 5b), making it a less useful threshold parameter (in the Appendix we show that this is also the case for various other local steepness parameters). Finally, for local slope ![]() $\eta _x$ it appears that there may be a threshold value of approximately
$\eta _x$ it appears that there may be a threshold value of approximately ![]() $0.55$–
$0.55$–![]() $0.60$ after which breaking occurs, causing values of local slope to increase sharply as the surface overturns (figure 5c). Prior to wave breaking local slope varies in a smooth oscillatory manner. Evidently, local slope
$0.60$ after which breaking occurs, causing values of local slope to increase sharply as the surface overturns (figure 5c). Prior to wave breaking local slope varies in a smooth oscillatory manner. Evidently, local slope ![]() $\eta _x\rightarrow -\infty$ as overturning occurs; the values of slope in figure 5(c) for breaking waves (small red dots) are taken one time step prior to overturning.
$\eta _x\rightarrow -\infty$ as overturning occurs; the values of slope in figure 5(c) for breaking waves (small red dots) are taken one time step prior to overturning.
Observed maximum local slope ![]() $\eta _x$ may be affected by the resolution of our simulations. Moreover, the onset of breaking may also change subtly depending on particle spacing at the wave crest. To establish the sensitivity of our results in figure 5(c) to the resolution of our numerical model, we rerun simulations of the largest non-breaking waves using the conformal mapping procedure outlined in § 4.1.2. The results of these simulations are shown as smaller dark grey dots in figure 5(c). For these simulations with significantly increased resolution near the wave crest, local slope still appears to approach a limit. The horizontal dashed line in figure 5(c) corresponds to a value of to
$\eta _x$ may be affected by the resolution of our simulations. Moreover, the onset of breaking may also change subtly depending on particle spacing at the wave crest. To establish the sensitivity of our results in figure 5(c) to the resolution of our numerical model, we rerun simulations of the largest non-breaking waves using the conformal mapping procedure outlined in § 4.1.2. The results of these simulations are shown as smaller dark grey dots in figure 5(c). For these simulations with significantly increased resolution near the wave crest, local slope still appears to approach a limit. The horizontal dashed line in figure 5(c) corresponds to a value of to ![]() $1/\tan ({\rm \pi} /3)$ (
$1/\tan ({\rm \pi} /3)$ (![]() $\approx$0.5774), which corresponds to a slope of
$\approx$0.5774), which corresponds to a slope of ![]() $60^\circ$ from the vertical (i.e. the limiting waveform of Stokes Reference Stokes1880).
$60^\circ$ from the vertical (i.e. the limiting waveform of Stokes Reference Stokes1880).
Simulations of wave groups with larger bandwidths will involve more waves of high frequency and short wavelength, and the modelling of these short waves will be affected more by the resolution of our simulations (![]() $N_p$). Thus, it follows that the differences observed between simulations performed using Configurations A and B are likely to be greater for larger bandwidths. This effect may also be the cause of the slight downward trend of
$N_p$). Thus, it follows that the differences observed between simulations performed using Configurations A and B are likely to be greater for larger bandwidths. This effect may also be the cause of the slight downward trend of ![]() $|\mathrm {min}(\eta _x)|$ with
$|\mathrm {min}(\eta _x)|$ with ![]() $\nu$ observed in figure 5(c) for the simulations performed using Configuration A.
$\nu$ observed in figure 5(c) for the simulations performed using Configuration A.
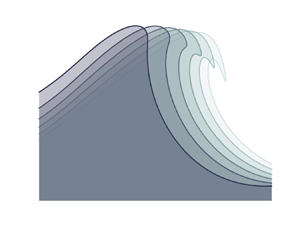
Surface elevation for the steepest simulated non-breaking waves based on constant-steepness spectra are plotted at the time of maximum local slope in figure 7. The horizontal axis for each plot has been shifted so that the wave crests are aligned in space. The inset plots show the vertically aligned surface elevations and local slope. The lines in figure 7 correspond to the grey markers in figure 5, and are coloured corresponding to their input bandwidth (increasing ![]() $\varDelta$ dark to light). This figure visualises the phenomena behind what we observe in figures 5(b) and 5(c). As bandwidth is increased, vertical asymmetry and zero-crossing wavelength of the waves both increase (
$\varDelta$ dark to light). This figure visualises the phenomena behind what we observe in figures 5(b) and 5(c). As bandwidth is increased, vertical asymmetry and zero-crossing wavelength of the waves both increase (![]() $k\downarrow$ and
$k\downarrow$ and ![]() $H\downarrow$), meaning that the overall waveforms appear quite different. However, the local (downward) slope of the wave crest front (
$H\downarrow$), meaning that the overall waveforms appear quite different. However, the local (downward) slope of the wave crest front (![]() $\eta _x<0$) across all bandwidths appear very similar; this is most evident in the inset plots of surface elevation and slope in figure 7. The time and position at which
$\eta _x<0$) across all bandwidths appear very similar; this is most evident in the inset plots of surface elevation and slope in figure 7. The time and position at which ![]() $|\mathrm {min}(\eta _x)|$ occurs for the simulations shown in figure 7 varies. The narrow-banded simulations modulate significantly and break well before intended linear focus, whereas the broad-banded simulations focus to the point of breaking in a predominantly linear manner. As a result, the breaking waves we create have varying resemblance to the linear focused wave groups we use to define initial conditions. Thus, we believe that results we present here are not specific to the focused wave group approach we use to generate initial conditions.
$|\mathrm {min}(\eta _x)|$ occurs for the simulations shown in figure 7 varies. The narrow-banded simulations modulate significantly and break well before intended linear focus, whereas the broad-banded simulations focus to the point of breaking in a predominantly linear manner. As a result, the breaking waves we create have varying resemblance to the linear focused wave groups we use to define initial conditions. Thus, we believe that results we present here are not specific to the focused wave group approach we use to generate initial conditions.

Figure 7. Surface elevation of maximally steep non-breaking focused wave groups based on constant-steepness spectra of different bandwidths, plotted as a function of ![]() $x$, which has been shifted to align the position of maximum surface elevation
$x$, which has been shifted to align the position of maximum surface elevation ![]() $\eta$ or slope
$\eta$ or slope ![]() $\eta _x$ for different bandwidths and made non-dimensional using
$\eta _x$ for different bandwidths and made non-dimensional using ![]() $\lambda _c$. Inset plots show vertically aligned surface elevation
$\lambda _c$. Inset plots show vertically aligned surface elevation ![]() $\eta -\eta _{max}$ (left) and local surface slope
$\eta -\eta _{max}$ (left) and local surface slope ![]() $\eta _x$ (right) at the wave crest. Line colours, dark to light, correspond to the bandwidth of the underlying spectrum, which ranges from
$\eta _x$ (right) at the wave crest. Line colours, dark to light, correspond to the bandwidth of the underlying spectrum, which ranges from ![]() $\varDelta =0.2$ to
$\varDelta =0.2$ to ![]() $1.4$. The red dotted line has a slope of
$1.4$. The red dotted line has a slope of ![]() $1/\tan ({\rm \pi} /3)$ (
$1/\tan ({\rm \pi} /3)$ (![]() $\approx$0.5774), which corresponds to the limiting waveform of Stokes (Reference Stokes1880).
$\approx$0.5774), which corresponds to the limiting waveform of Stokes (Reference Stokes1880).
4.3. Crest instability
If breaking is indeed triggered by the local slope reaching a critical value, this may indicate that breaking is being caused by a form of super-harmonic instability (Longuet-Higgins & Dommermuth Reference Longuet-Higgins and Dommermuth1997). Crest instabilities can occur when the surface slope reaches a critical value; this forms the basis of the breaking model in Pizzo & Melville (Reference Pizzo and Melville2019). To examine if such an instability is the cause of breaking in our simulations we compare the surface elevation of breaking and non-breaking waves for a given bandwidth (see also Longuet-Higgins Reference Longuet-Higgins1978). Specifically, we subtract the surface elevation of the largest non-breaking wave group ![]() $\eta ^\star _{-\Delta S}$ from the surface elevation of the smallest breaking wave group
$\eta ^\star _{-\Delta S}$ from the surface elevation of the smallest breaking wave group ![]() $\eta ^\star$ to calculate the free surface perturbation
$\eta ^\star$ to calculate the free surface perturbation ![]() $\Delta \eta ^\star =\eta ^\star -\eta ^\star _{-\Delta S}$ immediately prior to breaking (Tanaka et al. Reference Tanaka, Dold, Lewy and Peregrine1987). We do so for the wave groups we simulate based on constant-steepness spectra. If the free surface perturbation grows rapidly (e.g. exponentially), this indicates the presence of a crest instability. We note that these two wave groups (i.e.
$\Delta \eta ^\star =\eta ^\star -\eta ^\star _{-\Delta S}$ immediately prior to breaking (Tanaka et al. Reference Tanaka, Dold, Lewy and Peregrine1987). We do so for the wave groups we simulate based on constant-steepness spectra. If the free surface perturbation grows rapidly (e.g. exponentially), this indicates the presence of a crest instability. We note that these two wave groups (i.e. ![]() $\eta ^\star$ and
$\eta ^\star$ and ![]() $\eta ^\star _{-\Delta S}$) have a small difference in input steepness
$\eta ^\star _{-\Delta S}$) have a small difference in input steepness ![]() $\Delta S=5\times 10^{-5}$; this small difference in the initial conditions of the two wave groups
$\Delta S=5\times 10^{-5}$; this small difference in the initial conditions of the two wave groups ![]() $\Delta S$ may cause variation in
$\Delta S$ may cause variation in ![]() $\Delta \eta ^\star$ that is not a result of a crest instability. To quantify which part of
$\Delta \eta ^\star$ that is not a result of a crest instability. To quantify which part of ![]() $\Delta \eta ^\star$ is simply a result of different initial steepness, we also calculate the free surface perturbation between the largest non-breaking wave
$\Delta \eta ^\star$ is simply a result of different initial steepness, we also calculate the free surface perturbation between the largest non-breaking wave ![]() $\eta ^\star _{-\Delta S}$ and a wave group
$\eta ^\star _{-\Delta S}$ and a wave group ![]() $\eta ^\star _{-2\Delta S}$ with initial steepness
$\eta ^\star _{-2\Delta S}$ with initial steepness ![]() $S$ that is
$S$ that is ![]() $5\times 10^{-5}$ smaller again:
$5\times 10^{-5}$ smaller again: ![]() $\Delta \eta =\eta ^\star _{-\Delta S}-\eta ^\star _{-2\Delta S}$. Following Longuet-Higgins & Dommermuth (Reference Longuet-Higgins and Dommermuth1997), we calculate the growth of potential instabilities from the maximum difference at each instance in time,
$\Delta \eta =\eta ^\star _{-\Delta S}-\eta ^\star _{-2\Delta S}$. Following Longuet-Higgins & Dommermuth (Reference Longuet-Higgins and Dommermuth1997), we calculate the growth of potential instabilities from the maximum difference at each instance in time, ![]() $\mathrm {max}(\Delta \eta ^\star )-\mathrm {min}(\Delta \eta ^\star )$, of the free surface perturbation. In figure 8, we plot
$\mathrm {max}(\Delta \eta ^\star )-\mathrm {min}(\Delta \eta ^\star )$, of the free surface perturbation. In figure 8, we plot ![]() $\mathrm {max}(\Delta \eta ^\star )-\mathrm {min}(\Delta \eta ^\star )$ normalised by
$\mathrm {max}(\Delta \eta ^\star )-\mathrm {min}(\Delta \eta ^\star )$ normalised by ![]() $\mathrm {max}(\Delta \eta )-\mathrm {min}(\Delta \eta )$ as a function of time, where
$\mathrm {max}(\Delta \eta )-\mathrm {min}(\Delta \eta )$ as a function of time, where ![]() $t_{\eta _x}$ is the time at which surface slope reaches a value of
$t_{\eta _x}$ is the time at which surface slope reaches a value of ![]() $0.5774$. The normalised perturbation grows sharply around
$0.5774$. The normalised perturbation grows sharply around ![]() $t_{\eta _x}$ and is approximately constant prior to
$t_{\eta _x}$ and is approximately constant prior to ![]() $t_{\eta _x}$. This sudden increase is indicative of unstable behaviour, and suggest that surface slope may be subject to a type of (local) super-harmonic instability.
$t_{\eta _x}$. This sudden increase is indicative of unstable behaviour, and suggest that surface slope may be subject to a type of (local) super-harmonic instability.

Figure 8. Growth of a normalised surface perturbation as a function of time relative to the time ![]() $t_{\eta _x}$ at which surface slope reaches a (downward) value of
$t_{\eta _x}$ at which surface slope reaches a (downward) value of ![]() $0.5774$ for wave groups based on constant-steepness spectra. The different coloured markers, dark to light, correspond to the bandwidth of the underlying spectrum, which ranges from
$0.5774$ for wave groups based on constant-steepness spectra. The different coloured markers, dark to light, correspond to the bandwidth of the underlying spectrum, which ranges from ![]() $\varDelta =0.2$ to
$\varDelta =0.2$ to ![]() $1.4$.
$1.4$.
4.4. Spectral shape
Linear calculations performed in § 3 demonstrated that, alongside bandwidth, spectral shape has a significant influence on surface kinematics and local steepness of focused wave groups. In the following section we perform simulations of steep breaking and non-breaking focused wave groups to determine how spectral shape affects the relationship between breaking onset and bandwidth. As in § 3, we analyse simulations of focused wave groups based on constant-steepness, constant-amplitude and JONSWAP spectra. We consider global steepness (§ 4.4.1) and local slope (§ 4.4.2) in turn.
4.4.1. Global steepness
Figure 9 shows a regime diagram of breaking and non-breaking behaviour based on global steepness ![]() $S$ and bandwidth
$S$ and bandwidth ![]() $\nu$ for focused wave groups based on the different spectra we simulate. Grey markers denote simulations where no breaking was observed, red markers denote simulations where breaking was detected, and black dots denote simulations where
$\nu$ for focused wave groups based on the different spectra we simulate. Grey markers denote simulations where no breaking was observed, red markers denote simulations where breaking was detected, and black dots denote simulations where ![]() $B_x>0.855$ prior to overturning. The dashed black lines show (1.2) obtained by Pizzo et al. (Reference Pizzo, Murray, Smith and Lenain2021) for a constant-steepness spectrum.
$B_x>0.855$ prior to overturning. The dashed black lines show (1.2) obtained by Pizzo et al. (Reference Pizzo, Murray, Smith and Lenain2021) for a constant-steepness spectrum.

Figure 9. Regime diagram of breaking and non-breaking behaviour as a function of global steepness ![]() $S$ and bandwidth
$S$ and bandwidth ![]() $\nu$ for wave groups based on (a) JONSWAP and (b) constant-amplitude spectra. Grey markers indicate no breaking, red markers indicate overturning breaking and small black dots indicate
$\nu$ for wave groups based on (a) JONSWAP and (b) constant-amplitude spectra. Grey markers indicate no breaking, red markers indicate overturning breaking and small black dots indicate ![]() $B_x>0.855$. Additional coloured markers show comparable experimental (albeit finite-depth) results from Rapp & Melville (Reference Rapp and Melville1990) and Craciunescu & Christou (Reference Craciunescu and Christou2020). Dot-dashed lines show our exponential (black) and quadratic (green) parametric curves fitted to the breaking onset steepness (see table 3).
$B_x>0.855$. Additional coloured markers show comparable experimental (albeit finite-depth) results from Rapp & Melville (Reference Rapp and Melville1990) and Craciunescu & Christou (Reference Craciunescu and Christou2020). Dot-dashed lines show our exponential (black) and quadratic (green) parametric curves fitted to the breaking onset steepness (see table 3).
Table 3. Coefficients of parametric curves for breaking onset steepness as a function of bandwidth ![]() $\nu$ for focused wave groups based on JONSWAP and constant-amplitude spectra (see figure 9).
$\nu$ for focused wave groups based on JONSWAP and constant-amplitude spectra (see figure 9).

Before we discuss these simulations we emphasise that the range of bandwidths over which we simulate wave groups for each type of spectrum is different; thus, the horizontal axes limits for each panel in figures 9 and 11 are markedly different. For JONSWAP spectra varying ![]() $\gamma$ from 1 to 15 leads to variation in
$\gamma$ from 1 to 15 leads to variation in ![]() $\nu$ of approximately
$\nu$ of approximately ![]() $0.25$–
$0.25$–![]() $0.375$. Further increases in
$0.375$. Further increases in ![]() $\gamma$ leads to minimal reduction in
$\gamma$ leads to minimal reduction in ![]() $\nu$. For constant-steepness and constant-amplitude spectra we are able to vary the bandwidth over a similar range (
$\nu$. For constant-steepness and constant-amplitude spectra we are able to vary the bandwidth over a similar range (![]() $\nu =0.05$–
$\nu =0.05$–![]() $0.4$).
$0.4$).
In figure 9, the breaking threshold in terms of global steepness ![]() $S$ for focused wave groups based on JONSWAP spectra increases with bandwidth, but does not follow (1.2). For wave groups based on constant-amplitude spectra, initially there is a slight increase then a leveling off of the breaking threshold
$S$ for focused wave groups based on JONSWAP spectra increases with bandwidth, but does not follow (1.2). For wave groups based on constant-amplitude spectra, initially there is a slight increase then a leveling off of the breaking threshold ![]() $S$ with bandwidth. Both spectral shapes, JONSWAP and constant-amplitude, show similar behaviour, leveling off for large values of
$S$ with bandwidth. Both spectral shapes, JONSWAP and constant-amplitude, show similar behaviour, leveling off for large values of ![]() $\nu$, but at two different values,
$\nu$, but at two different values, ![]() $S=0.34$ and
$S=0.34$ and ![]() $0.26$, respectively. Table 3 lists parametric curves we have obtained by fitting two different functional forms to the data for the different spectra in figure 9.
$0.26$, respectively. Table 3 lists parametric curves we have obtained by fitting two different functional forms to the data for the different spectra in figure 9.
As the next order spectral moment from bandwidth, spectral skewness may provide a way to characterise the influence spectral shape has on breaking onset. Spectra with a high-frequency tail (i.e. JONSWAP) will have positive skewness, as do constant-steepness spectra. For a constant-amplitude spectrum, skewness is zero, which may help explain the reduced variation of ![]() $S$ observed in figure 9(b). In figure 10 we plot 2-D projections of the regime diagram of breaking and non-breaking behaviour for all the simulations we perform in terms of bandwidth
$S$ observed in figure 9(b). In figure 10 we plot 2-D projections of the regime diagram of breaking and non-breaking behaviour for all the simulations we perform in terms of bandwidth ![]() $\nu$, skewness
$\nu$, skewness ![]() $\varGamma$, calculated as the standardised third central moment of the energy spectrum and global steepness
$\varGamma$, calculated as the standardised third central moment of the energy spectrum and global steepness ![]() $S$. The black dashed lines delineate breaking and non-breaking behaviour for each of the three types of spectra simulated. From the limited coverage of the parameter space that our simulations provide, it does not appear possible to fit a smooth surface to delineate breaking and non-breaking behaviour.
$S$. The black dashed lines delineate breaking and non-breaking behaviour for each of the three types of spectra simulated. From the limited coverage of the parameter space that our simulations provide, it does not appear possible to fit a smooth surface to delineate breaking and non-breaking behaviour.

Figure 10. 2-D projections of the 3-D regime diagram of breaking and non-breaking behaviour in terms of global steepness ![]() $S$, skewness
$S$, skewness ![]() $\varGamma$, bandwidth
$\varGamma$, bandwidth ![]() $\nu$, showing breaking (red) and non-breaking (grey) behaviour for all the focused wave groups simulated. Vertical partially transparent planes show the limits of the parameter range for each spectral shape (see the labels in panel c). The breaking threshold is delineated using black dashed lines. All panels show different projections of the same plot.
$\nu$, showing breaking (red) and non-breaking (grey) behaviour for all the focused wave groups simulated. Vertical partially transparent planes show the limits of the parameter range for each spectral shape (see the labels in panel c). The breaking threshold is delineated using black dashed lines. All panels show different projections of the same plot.
4.4.2. Local slope
In figure 11 we plot maximum values of local slope ![]() $\eta _x$ measured during the numerical simulations of wave groups based on JONSWAP and constant-amplitude spectra. As observed for focused wave groups based on constant-steepness spectra, maximum local steepness for non-breaking waves appears to also approach the limit
$\eta _x$ measured during the numerical simulations of wave groups based on JONSWAP and constant-amplitude spectra. As observed for focused wave groups based on constant-steepness spectra, maximum local steepness for non-breaking waves appears to also approach the limit ![]() $1/\tan ({\rm \pi} /3)$, i.e. a slope of
$1/\tan ({\rm \pi} /3)$, i.e. a slope of ![]() $60^\circ$. This suggests that a breaking threshold based on local slope may be more universal than one based on global steepness, being valid across a range of bandwidths and spectral shapes.
$60^\circ$. This suggests that a breaking threshold based on local slope may be more universal than one based on global steepness, being valid across a range of bandwidths and spectral shapes.

Figure 11. Maximum local slope ![]() $|\mathrm {min}(\eta _x)|$ as a function of bandwidth for (a) JONSWAP and (b) constant-amplitude spectra. Red and grey markers correspond to simulations where breaking has and has not occurred, respectively. For breaking simulations
$|\mathrm {min}(\eta _x)|$ as a function of bandwidth for (a) JONSWAP and (b) constant-amplitude spectra. Red and grey markers correspond to simulations where breaking has and has not occurred, respectively. For breaking simulations ![]() $\eta _x$ was measured one time step prior to overturning. The horizontal dashed lines correspond to
$\eta _x$ was measured one time step prior to overturning. The horizontal dashed lines correspond to ![]() $1/\tan ({\rm \pi} /3)$, i.e. a slope of
$1/\tan ({\rm \pi} /3)$, i.e. a slope of ![]() $60^\circ$.
$60^\circ$.
4.5. Breaking onset detection
We have found that the relationship between spectral shape and wave breaking onset is too complex to parameterise in a simple manner using a spectral parameters (i.e. ![]() $\nu$ and
$\nu$ and ![]() $\varGamma$) and global steepness
$\varGamma$) and global steepness ![]() $S$. Nevertheless, local parameters may still be used to indicate when breaking will occur on a wave-by-wave basis. While less generally applicable and less predictive, readily observable local parameters that can detect breaking onset are still highly useful.
$S$. Nevertheless, local parameters may still be used to indicate when breaking will occur on a wave-by-wave basis. While less generally applicable and less predictive, readily observable local parameters that can detect breaking onset are still highly useful.
As mentioned previously, the parameter ![]() $B_x$ has been shown to be a promising means by which to detect the onset of breaking of forced and unforced waves, in experiments (Saket et al. Reference Saket, Peirson, Banner, Barthelemy and Allis2017), numerical simulations of 2-D and moderately spread 3-D waves (Barthelemy et al. Reference Barthelemy, Banner, Peirson, Fedele, Allis and Dias2018), on deep and shallow water depths (Derakhti et al. Reference Derakhti, Kirby, Banner, Grilli and Thomson2020), and in the presence of constant vorticity (Touboul & Banner Reference Touboul and Banner2021). In figures 5 and 11 we have shown that local maximum surface slope, defined as
$B_x$ has been shown to be a promising means by which to detect the onset of breaking of forced and unforced waves, in experiments (Saket et al. Reference Saket, Peirson, Banner, Barthelemy and Allis2017), numerical simulations of 2-D and moderately spread 3-D waves (Barthelemy et al. Reference Barthelemy, Banner, Peirson, Fedele, Allis and Dias2018), on deep and shallow water depths (Derakhti et al. Reference Derakhti, Kirby, Banner, Grilli and Thomson2020), and in the presence of constant vorticity (Touboul & Banner Reference Touboul and Banner2021). In figures 5 and 11 we have shown that local maximum surface slope, defined as ![]() $|\mathrm {min}(\eta _x)|$, may approach a threshold prior to breaking that is independent of spectral shape and bandwidth. It appears that local surface slope at the wave crest
$|\mathrm {min}(\eta _x)|$, may approach a threshold prior to breaking that is independent of spectral shape and bandwidth. It appears that local surface slope at the wave crest ![]() $|\mathrm {min}(\eta _x)|\rightarrow 1/\tan ({\rm \pi} /3)$ and may be self-similar for maximally steep waves (cf. figure 7). This local maximum slope is the same maximum slope predicted by Stokes (Reference Stokes1880) for the limiting waveform of progressive waves on deep water. Stokes's prediction of a
$|\mathrm {min}(\eta _x)|\rightarrow 1/\tan ({\rm \pi} /3)$ and may be self-similar for maximally steep waves (cf. figure 7). This local maximum slope is the same maximum slope predicted by Stokes (Reference Stokes1880) for the limiting waveform of progressive waves on deep water. Stokes's prediction of a ![]() $120^\circ$-corner flow at the crest of the limiting waveform, corresponds to a kinematic limit where
$120^\circ$-corner flow at the crest of the limiting waveform, corresponds to a kinematic limit where ![]() $u/C=1$. Thus, there may be an inherent link between
$u/C=1$. Thus, there may be an inherent link between ![]() $|\mathrm {min}(\eta _x)|$ and
$|\mathrm {min}(\eta _x)|$ and ![]() $B_x$.
$B_x$.
In many applications, particularly in the field or the laboratory, measuring local slope may be more straightforward than measuring surface kinematics. Therefore, ![]() $|\mathrm {min}(\eta _x)|$ may provide an alternative means to
$|\mathrm {min}(\eta _x)|$ may provide an alternative means to ![]() $B_x$, to detect the onset of breaking in such scenarios. In figure 12 we plot breaking (red) and non-breaking (grey) values of
$B_x$, to detect the onset of breaking in such scenarios. In figure 12 we plot breaking (red) and non-breaking (grey) values of ![]() $|\mathrm {min}(\eta _x)|$ (panel a) and
$|\mathrm {min}(\eta _x)|$ (panel a) and ![]() $B_x$ (panel b) as a function of input global steepness
$B_x$ (panel b) as a function of input global steepness ![]() $S$ for all the simulations we have performed. Threshold values of
$S$ for all the simulations we have performed. Threshold values of ![]() $|\mathrm {min}(\eta _x)|=1/\tan ({\rm \pi} /3)$ and
$|\mathrm {min}(\eta _x)|=1/\tan ({\rm \pi} /3)$ and ![]() $B_x=0.855$ are shown as black dashed lines. In panel (c) box plots show the range of values both parameters take for breaking and non-breaking simulations. The top and bottom of each box correspond to the 25th and 75th percentiles, the central marks corresponds to the median, and the whiskers correspond to the range of values. Our simulations show that
$B_x=0.855$ are shown as black dashed lines. In panel (c) box plots show the range of values both parameters take for breaking and non-breaking simulations. The top and bottom of each box correspond to the 25th and 75th percentiles, the central marks corresponds to the median, and the whiskers correspond to the range of values. Our simulations show that ![]() $|\mathrm {min}(\eta _x)|$ may function well as a threshold parameter as the separation between breaking and non-breaking is large and indeed larger than for
$|\mathrm {min}(\eta _x)|$ may function well as a threshold parameter as the separation between breaking and non-breaking is large and indeed larger than for ![]() $B_x$. The range of values of
$B_x$. The range of values of ![]() $|\mathrm {min}(\eta _x)|$ takes also does not exceed the limit
$|\mathrm {min}(\eta _x)|$ takes also does not exceed the limit ![]() $|\mathrm {min}(\eta _x)|=1/\tan ({\rm \pi} /3)$.
$|\mathrm {min}(\eta _x)|=1/\tan ({\rm \pi} /3)$.

Figure 12. Breaking onset threshold behaviour for all simulated wave groups, (a) maximum local slope ![]() $|\mathrm {min}(\eta _x)|$ and (b) the maximum value of parameter
$|\mathrm {min}(\eta _x)|$ and (b) the maximum value of parameter ![]() $B_x$ measured in each simulation plotted as a function input global steepness; in panel (c) box and whiskers show the range of breaking and non-breaking values for each parameter. Breaking and non-breaking waves are denoted by grey and red lines, respectively. Black dashed lines show values of
$B_x$ measured in each simulation plotted as a function input global steepness; in panel (c) box and whiskers show the range of breaking and non-breaking values for each parameter. Breaking and non-breaking waves are denoted by grey and red lines, respectively. Black dashed lines show values of ![]() $|\mathrm {min}(\eta _x)|=1/\tan ({\rm \pi} /3)$ and
$|\mathrm {min}(\eta _x)|=1/\tan ({\rm \pi} /3)$ and ![]() $B_x=0.855$; in panel (d) histograms show the times at which
$B_x=0.855$; in panel (d) histograms show the times at which ![]() $|\mathrm {min}(\eta _x)|=1/\tan ({\rm \pi} /3)$ and
$|\mathrm {min}(\eta _x)|=1/\tan ({\rm \pi} /3)$ and ![]() $B_x=0.855$ relative to
$B_x=0.855$ relative to ![]() $t^\star$ the time at which the surface first becomes vertical, the histogram bars are scaled by the number of values in each bin divided by the total number of simulations where breaking occurred.
$t^\star$ the time at which the surface first becomes vertical, the histogram bars are scaled by the number of values in each bin divided by the total number of simulations where breaking occurred.
In a recent paper, Boettger et al. (Reference Boettger, Keating, Banner, Morison and Barthélémy2023) examined the flux of the maximum kinetic energy ![]() $D_b E_k/Dt$ at the crest of breaking and non-breaking waves, and found that breaking occurred when
$D_b E_k/Dt$ at the crest of breaking and non-breaking waves, and found that breaking occurred when ![]() $D_b E_k/Dt \geqslant 0.235$ for 2-D chirped wave packets on intermediate and deep water (
$D_b E_k/Dt \geqslant 0.235$ for 2-D chirped wave packets on intermediate and deep water (![]() $k_pd=1.07\unicode{x2013}3.14$). This threshold occurs approximately 0.25 periods prior to
$k_pd=1.07\unicode{x2013}3.14$). This threshold occurs approximately 0.25 periods prior to ![]() $B_x=0.855$ and may potentially be an indication of irreversible breaking inception, which precedes breaking onset. In figure 12(d) we plot the times at which
$B_x=0.855$ and may potentially be an indication of irreversible breaking inception, which precedes breaking onset. In figure 12(d) we plot the times at which ![]() $\eta _x=-0.5774$ and
$\eta _x=-0.5774$ and ![]() $B_x=0855$ occur relative to
$B_x=0855$ occur relative to ![]() $t^\star$, the time at which the surface first becomes vertical, for the breaking waves we have simulated. The
$t^\star$, the time at which the surface first becomes vertical, for the breaking waves we have simulated. The ![]() $B_x$ threshold is exceeded at around
$B_x$ threshold is exceeded at around ![]() $-0.05T_c$, and the slope threshold is exceeded at between approximately
$-0.05T_c$, and the slope threshold is exceeded at between approximately ![]() $-0.5T_c$ and
$-0.5T_c$ and ![]() $-0.1T_c$. The times at which
$-0.1T_c$. The times at which ![]() $\eta _x=-0.5774$ are similar to the times at which
$\eta _x=-0.5774$ are similar to the times at which ![]() $D_b E_k/Dt =0.235$ in figure 10 of Boettger et al. (Reference Boettger, Keating, Banner, Morison and Barthélémy2023). Thus, there may be a link between a surface-slope-based and an energy-based signature of breaking inception. In our simulations the time at which
$D_b E_k/Dt =0.235$ in figure 10 of Boettger et al. (Reference Boettger, Keating, Banner, Morison and Barthélémy2023). Thus, there may be a link between a surface-slope-based and an energy-based signature of breaking inception. In our simulations the time at which ![]() $\eta _x=-0.5774$ is a function of spectral bandwidth with
$\eta _x=-0.5774$ is a function of spectral bandwidth with ![]() $(t-t^\star )/T_c$ reducing slightly as bandwidth increases, which explains some of the scatter in figure 12(d). On the other hand, in our simulations it appears that the time at which
$(t-t^\star )/T_c$ reducing slightly as bandwidth increases, which explains some of the scatter in figure 12(d). On the other hand, in our simulations it appears that the time at which ![]() $B_x=0.855$ occurs is largely unaffected by bandwidth.
$B_x=0.855$ occurs is largely unaffected by bandwidth.
At certain scales surface tension can create parasitic capillary waves (PCWs) that form at steep wave crests, affecting wave geometry and potentially the onset and dynamics of wave breaking (see Dias & Kharif (Reference Dias and Kharif1999) for a review of some of these effects). In Duncan (Reference Duncan2001), the formation of PCWs on spilling breaking waves is reviewed, suggesting that PCWs can occur on breaking waves with wavelengths of around 1 m and below. In experiments performed using clean water, Diorio, Liu & Duncan (Reference Diorio, Liu and Duncan2009) observed PCW formation on spilling breaking waves that were generated by dispersive focusing with characteristic wavelengths as large as ![]() $1.2$ m. Boettger et al. (Reference Boettger, Keating, Banner, Morison and Barthélémy2023) performed computational fluid dynamics (CFD) simulations of 2-D breaking waves, concluding that the effects of surface tension were negligible on the energetics of breaking onset and that small amounts of viscous dissipation occurred at the wave crest (
$1.2$ m. Boettger et al. (Reference Boettger, Keating, Banner, Morison and Barthélémy2023) performed computational fluid dynamics (CFD) simulations of 2-D breaking waves, concluding that the effects of surface tension were negligible on the energetics of breaking onset and that small amounts of viscous dissipation occurred at the wave crest (![]() $\lambda _p=0.85$ m,
$\lambda _p=0.85$ m, ![]() ${Re}=4\times 10^4$). The studies we have referenced above examine a mixture of breaking and non-breaking waves. Deike, Popinet & Melville (Reference Deike, Popinet and Melville2015) performed DNS simulations with
${Re}=4\times 10^4$). The studies we have referenced above examine a mixture of breaking and non-breaking waves. Deike, Popinet & Melville (Reference Deike, Popinet and Melville2015) performed DNS simulations with ![]() ${Bo}=10^1\unicode{x2013}10^4$ to systematically assess how surface tension affects the onset of wave breaking. They only observed PCWs below the critical Bond number
${Bo}=10^1\unicode{x2013}10^4$ to systematically assess how surface tension affects the onset of wave breaking. They only observed PCWs below the critical Bond number ![]() ${Bo}_c=67$ (
${Bo}_c=67$ (![]() $\lambda =0.14$ m). These simulations also showed that for
$\lambda =0.14$ m). These simulations also showed that for ![]() ${Bo}\gg 10^2$ the effects of surface tension are small and the steepness at which wave breaking occurs is Bond number independent; a Bond number of
${Bo}\gg 10^2$ the effects of surface tension are small and the steepness at which wave breaking occurs is Bond number independent; a Bond number of ![]() $10^3$ corresponds to waves of approximately
$10^3$ corresponds to waves of approximately ![]() $0.5$ s in period or 0.4 m in wavelength (
$0.5$ s in period or 0.4 m in wavelength (![]() ${Bo}=\Delta \rho g/(\gamma k^2)$, assuming
${Bo}=\Delta \rho g/(\gamma k^2)$, assuming ![]() $\Delta \rho =1.0\times 10^3\ {\rm kg}\ {\rm m}^{-3}$ and
$\Delta \rho =1.0\times 10^3\ {\rm kg}\ {\rm m}^{-3}$ and ![]() $\gamma =7.2\times 10^{-2}\ {\rm N}\ {\rm m}^{-1}$). The slope-based threshold we have observed may be affected by the formation of PCWs at small length scales (
$\gamma =7.2\times 10^{-2}\ {\rm N}\ {\rm m}^{-1}$). The slope-based threshold we have observed may be affected by the formation of PCWs at small length scales (![]() $\lambda \lesssim 1\ {\rm m}$), where surface tension becomes important. This could be assessed through separate simulations that include the effects of surface tension or physical experiments, either of which constitute a considerable undertaking and go beyond the scope of the current paper.
$\lambda \lesssim 1\ {\rm m}$), where surface tension becomes important. This could be assessed through separate simulations that include the effects of surface tension or physical experiments, either of which constitute a considerable undertaking and go beyond the scope of the current paper.
5. Conclusions
Existing studies of wave breaking present a range of sometimes conflicting conclusions on how spectral bandwidth affects the onset of wave breaking; in many of these studies studying the effect of bandwidth on breaking onset may not have been the primary focus. Pizzo & Melville (Reference Pizzo and Melville2019) and Pizzo et al. (Reference Pizzo, Murray, Smith and Lenain2021) addressed this question directly analytically (see also Pizzo & Melville Reference Pizzo and Melville2016) and numerically and found that breaking onset occurs at increasing steepness as bandwidth is increased. Wu & Yao (Reference Wu and Yao2004) addressed the same problem experimentally and seemingly drew the opposite conclusion. Herein, we have performed linear and fully nonlinear simulations of 2-D focused wave groups to elucidate the potential causes of these differences, and gain a broader understanding of how bandwidth and spectral shape affect wave breaking onset. Linear calculations show that, on a kinematic basis alone, bandwidth will cause the onset of breaking to occur at lower global steepness ![]() $S$. For a constant global steepness
$S$. For a constant global steepness ![]() $S$, bandwidth can cause apparent local steepness
$S$, bandwidth can cause apparent local steepness ![]() $kH/2$ to reduce by as much as
$kH/2$ to reduce by as much as ![]() $80\,\%$. Thus, even on a linear basis, the different measures of steepness used (local versus global) may serve to explain the differences in perceived breaking thresholds as a function of bandwidth in the existing literature.
$80\,\%$. Thus, even on a linear basis, the different measures of steepness used (local versus global) may serve to explain the differences in perceived breaking thresholds as a function of bandwidth in the existing literature.
For fully nonlinear simulations of maximally steep focused wave groups based on constant-steepness spectra of varying bandwidth, we reproduce the breaking threshold in Pizzo et al. (Reference Pizzo, Murray, Smith and Lenain2021) and obtain qualitatively similar results to Wu & Yao (Reference Wu and Yao2004). Our numerical results demonstrate that the definition of steepness is likely the main cause of the difference between these two studies. In addition, we find that local steepness ![]() $kH/2$ is not a robust parameter because of fluctuations in zero-crossing wavelength and does not demarcate breaking and non-breaking wave groups effectively.
$kH/2$ is not a robust parameter because of fluctuations in zero-crossing wavelength and does not demarcate breaking and non-breaking wave groups effectively.
For wave groups based on JONSWAP and constant-amplitude spectra, breaking onset steepness ![]() $S$ increases with bandwidth. Variation in breaking onset steepness is minimal for JONSWAP spectra of
$S$ increases with bandwidth. Variation in breaking onset steepness is minimal for JONSWAP spectra of ![]() $\gamma =1$ to
$\gamma =1$ to ![]() $5$ (
$5$ (![]() $\nu =0.2$ to
$\nu =0.2$ to ![]() $0.1$), and for all but the most narrow-banded constant-amplitude spectra wave groups. Global steepness
$0.1$), and for all but the most narrow-banded constant-amplitude spectra wave groups. Global steepness ![]() $S$ demarcates breaking and non-breaking behaviour as a function of bandwidth
$S$ demarcates breaking and non-breaking behaviour as a function of bandwidth ![]() $\nu$ for all the spectral shapes we examine. Alongside bandwidth, we demonstrate that spectral shape affects the onset of wave breaking. However, we find that skewness and bandwidth alone do not provide enough information to parameterise the effects spectral shape has on breaking onset when considering global steepness
$\nu$ for all the spectral shapes we examine. Alongside bandwidth, we demonstrate that spectral shape affects the onset of wave breaking. However, we find that skewness and bandwidth alone do not provide enough information to parameterise the effects spectral shape has on breaking onset when considering global steepness ![]() $S$.
$S$.
It may be possible to use additional spectral moments to try and parameterise breaking onset in a global (spectral) sense; though this may not be necessary in practice as for JONSWAP spectra, which best reflect ocean wave conditions, there is very little variation in breaking onset steepness ![]() $S$ at values of
$S$ at values of ![]() $\gamma =1\unicode{x2013}5$. Therefore, for the majority of sea states there may not be a great deal of variation in breaking onset over the range of realistic bandwidths.
$\gamma =1\unicode{x2013}5$. Therefore, for the majority of sea states there may not be a great deal of variation in breaking onset over the range of realistic bandwidths.
Returning to figure 2, the conclusions we have drawn help to explain the scatter we observe in wave breaking onset steepness; with the definition of steepness and differences in underlying spectral shapes being the main causes of disagreement. If steepness is defined locally, breaking onset steepness will not necessarily collapse onto a single parameterised curve. If steepness is defined globally, different spectral shapes will results in different breaking onset parameterisations as a function of bandwidth. For the question of how spectral bandwidth affects wave breaking onset in a general sense, our study shows, if defined globally, breaking onset steepness increases with bandwidth, and if defined locally (broadly speaking), breaking onset steepness decreases with bandwidth.
In contrast to local ![]() $kH/2$ and global steepness
$kH/2$ and global steepness ![]() $S$, the local slope
$S$, the local slope ![]() $\eta _x$ of maximally steep non-breaking waves varies little as a function of bandwidth and approaches a threshold of
$\eta _x$ of maximally steep non-breaking waves varies little as a function of bandwidth and approaches a threshold of ![]() $1/\tan ({\rm \pi} /3)\approx 0.5774$ (corresponding to the limiting waveform of Stokes Reference Stokes1847). This wave breaking threshold based on local slope is observed for all of the wave groups we examine regardless of their spectral shapes.
$1/\tan ({\rm \pi} /3)\approx 0.5774$ (corresponding to the limiting waveform of Stokes Reference Stokes1847). This wave breaking threshold based on local slope is observed for all of the wave groups we examine regardless of their spectral shapes.
Concluding, we have found that breaking onset occurs at the same threshold value of the local slope (![]() $\partial \eta /\partial x$) regardless of the underlying spectrum of the waves. This is a remarkable result, which we do not believe has been reported before. Our simulations have demonstrated that
$\partial \eta /\partial x$) regardless of the underlying spectrum of the waves. This is a remarkable result, which we do not believe has been reported before. Our simulations have demonstrated that ![]() $|\mathrm {min}(\eta _x)|$ may provide an alternative breaking onset threshold to the ratio of fluid and crest speed,
$|\mathrm {min}(\eta _x)|$ may provide an alternative breaking onset threshold to the ratio of fluid and crest speed, ![]() $B_x=u/C$; the threshold
$B_x=u/C$; the threshold ![]() $|\mathrm {min}(\eta _x)|$ may be easier to apply in certain scenarios, for example when fluid velocities are unknown. We note, however, that the threshold we present may be limited to 2-D deep-water conditions, which is not the case for
$|\mathrm {min}(\eta _x)|$ may be easier to apply in certain scenarios, for example when fluid velocities are unknown. We note, however, that the threshold we present may be limited to 2-D deep-water conditions, which is not the case for ![]() $B_x$. This slope-based threshold may also be influenced by the effects of surface tension, potentially limiting its applicability to wavelengths
$B_x$. This slope-based threshold may also be influenced by the effects of surface tension, potentially limiting its applicability to wavelengths ![]() $>1$ m, where such effects are less important. Similarity in the crest shape of breaking waves may be linked to a kinematic description of breaking (and, thus, to a given value of
$>1$ m, where such effects are less important. Similarity in the crest shape of breaking waves may be linked to a kinematic description of breaking (and, thus, to a given value of ![]() $B_x$ or
$B_x$ or ![]() $D_b E_k/Dt$ (Boettger et al. Reference Boettger, Keating, Banner, Morison and Barthélémy2023)) which, alongside the robustness and generality of a slope-based threshold, should be examined further.
$D_b E_k/Dt$ (Boettger et al. Reference Boettger, Keating, Banner, Morison and Barthélémy2023)) which, alongside the robustness and generality of a slope-based threshold, should be examined further.
Funding
This research was performed in part through funding by EPSRC-SFI grant EP/V013114/1. N.P. was partially supported by a grant from NSF OCE-2219752.
Declaration of interests
The authors report no conflict of interest.
Appendix. Alternative definitions of local steepness
In figure 13 we illustrate how various alternative measures of local steepness function as parameters to delineate breaking and non-breaking behaviour. Panels (a–c) show crest amplitude made non-dimensional by zero-crossing wavenumbers based on total, crest and crest-front wavelengths. Panels (d–f) show local steepness using zero-down- and zero-up-crossing wave heights and wavenumbers. All of these local steepness parameters involve length scales that are estimated using zero-crossings, which leads to quite unstable values of wavenumber that fluctuate significantly in time (see figure 6) and do not necessarily represent wave crest geometry well. All panes except (e) show steepness measured ![]() $\pm T_c/2$ either side of the time of maximum slope
$\pm T_c/2$ either side of the time of maximum slope ![]() $|\min (\eta _x)|$; the values of steepness in panel (e) correspond to maxima observed without this time constraint. All of these parameters are ineffective in delineating breaking and non-breaking behaviour, even with additional time constraints. Crest front steepness, which is the closest to local slope perhaps appears to be the best local steepness measure when it comes to delineating breaking non-breaking behaviour. However, in panel (c) there are still many breaking waves with crest-front steepness lower than non-breaking waves.
$|\min (\eta _x)|$; the values of steepness in panel (e) correspond to maxima observed without this time constraint. All of these parameters are ineffective in delineating breaking and non-breaking behaviour, even with additional time constraints. Crest front steepness, which is the closest to local slope perhaps appears to be the best local steepness measure when it comes to delineating breaking non-breaking behaviour. However, in panel (c) there are still many breaking waves with crest-front steepness lower than non-breaking waves.

Figure 13. Various measures of maximum local steepness as a function of bandwidth for all simulated wave groups. Red and grey markers correspond to simulations where breaking respectively has or has not occurred, the grey markers have been made partially transparent to aid clarity where they overlap with the red markers. For breaking simulations local steepness was measured prior to overturning.