Article contents
The influence of spanwise confinement on round fountains
Published online by Cambridge University Press: 26 April 2018
Abstract
We study experimentally the effects of spanwise confinement on turbulent miscible fountains issuing from a round source of radius 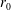 $r_{0}$. A dense saline solution is ejected vertically upwards into a fresh-water environment between two parallel plates, separated by a gap of width
$r_{0}$. A dense saline solution is ejected vertically upwards into a fresh-water environment between two parallel plates, separated by a gap of width 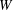 $W$, which provide restraint in the spanwise direction. The resulting fountain, if sufficiently forced, rapidly attaches to the side plates as it rises and is therefore ‘confined’. We report on experiments for five confinement ratios
$W$, which provide restraint in the spanwise direction. The resulting fountain, if sufficiently forced, rapidly attaches to the side plates as it rises and is therefore ‘confined’. We report on experiments for five confinement ratios 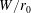 $W/r_{0}$, spanning from strongly confined (
$W/r_{0}$, spanning from strongly confined (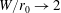 $W/r_{0}\rightarrow 2$) to weakly confined (
$W/r_{0}\rightarrow 2$) to weakly confined (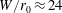 $W/r_{0}\approx 24$), and for source Froude numbers
$W/r_{0}\approx 24$), and for source Froude numbers 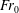 $Fr_{0}$ ranging between
$Fr_{0}$ ranging between 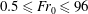 $0.5\leqslant Fr_{0}\leqslant 96$. Four distinct flow regimes are observed across which the relative importance of confinement, as manifested by the formation and growth of quasi-two-dimensional structures, varies. The onset of each regime is established as a function of both
$0.5\leqslant Fr_{0}\leqslant 96$. Four distinct flow regimes are observed across which the relative importance of confinement, as manifested by the formation and growth of quasi-two-dimensional structures, varies. The onset of each regime is established as a function of both 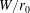 $W/r_{0}$ and
$W/r_{0}$ and 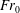 $Fr_{0}$. From our analysis of the time-averaged rise heights, we introduce a ‘confined’ Froude number
$Fr_{0}$. From our analysis of the time-averaged rise heights, we introduce a ‘confined’ Froude number 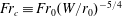 $Fr_{c}\equiv Fr_{0}(W/r_{0})^{-5/4}$, which encompasses the effects of confinement and acts as the governing parameter for confined fountains. First-order statistics extracted from the flow visualisation, such as the time-averaged rise height and lateral excursions, lend further insight into the flow and support the proposed classification into regimes. For highly confined fountains, the flow becomes quasi-two-dimensional and, akin to quasi-two-dimensional jets and plumes, flaps (or meanders). The characteristic frequency of this flapping motion, identified through an ‘eddy counting’ approach, is non-dimensionalised to a Strouhal number of
$Fr_{c}\equiv Fr_{0}(W/r_{0})^{-5/4}$, which encompasses the effects of confinement and acts as the governing parameter for confined fountains. First-order statistics extracted from the flow visualisation, such as the time-averaged rise height and lateral excursions, lend further insight into the flow and support the proposed classification into regimes. For highly confined fountains, the flow becomes quasi-two-dimensional and, akin to quasi-two-dimensional jets and plumes, flaps (or meanders). The characteristic frequency of this flapping motion, identified through an ‘eddy counting’ approach, is non-dimensionalised to a Strouhal number of 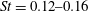 $St=0.12{-}0.16$, consistent with frequencies found in quasi-two-dimensional jets and plumes.
$St=0.12{-}0.16$, consistent with frequencies found in quasi-two-dimensional jets and plumes.
JFM classification
- Type
- JFM Papers
- Information
- Copyright
- © 2018 Cambridge University Press
References
Debugne et al. supplementary movie 1
Weakly-confined fountains: snippet of experiment conducted at Fr0=5.4, W/r0= 4.7 (cf. figure 2).
Debugne et al. supplementary movie 2
symmetric fountains: snippet of experiment conducted at Fr0=8.9, W/r0=4.7 (cf. figure 3).
Debugne et al. supplementary movie 3
Transitional fountains: snippet of experiment conducted at Fr0=14.0, W/r0=4.7 (cf. figure 4).
Debugne et al. supplementary movie 4
Meandering fountains: snippet of experiment conducted at Fr0=24.5, W/r0=4.7 (cf. figure 5).
- 7
- Cited by



